Научный электронный журнал КубГАУ . № 05(7), 2004
УДК 574.5+578.087.1+51.001.572
КОГНИТИВНАЯ СТРУКТУРИЗАЦИЯ И ФОРМАЛИЗАЦИЯ ЗАДАЧИ УПРАВЛЕНИЯ КАЧЕСТВОМ ГРУНТОВЫХ ВОД НА РИСОВЫХ ОРОСИТЕЛЬНЫХ СИСТЕМАХ
Сафронова Т.И. – к. т. н., доцент
Луценко Е.В. – д. э. н., к. т. н., профессор
Кубанский государственный аграрный университет
В статье осуществлена когнитивная структуризация и формализация задачи управления степенью минерализации и глубиной залегания грунтовых вод, в результате чего разработаны классификационные и описательные шкалы и градации, с использованием которых закодирована и импортирована в программную систему обучающая выборка.
1. Когнитивная структуризация предметной области
1.1. Задачи когнитивной структуризации
Проблема исследования, её актуальность, идея решения приведены в [2].
В данной работе под когнитивной структуризацией предметной области понимается процесс ее познания, который осуществляется на основе системного подхода, в соответствии с которым объект познания рассматривается как система, имеющая сложное многоуровневое иерархическое строение. Когнитивная структуризация предметной области – это начальный этап синтеза модели, подготавливающий формализацию и предшествующий ей [1].
При когнитивной структуризации:
– выделяются целевые параметры системы, т.е. ее желательные и нежелательные будущие состояния, характеризующие ее на макроуровне;
– определяется система факторов, детерминирующих эти будущие состояния.
Как факторы могут рассматриваться и факторы окружающей среды, и технологические факторы, и параметры системы на низких уровнях ее иерархической структуры.
Основываясь на исходных данных, приведенных в работе [2], выделим для исследования в модели будущие состояния минерализации и уровней грунтовых вод (МиУГВ) и факторы.
1.2. Определение будущих состояний объекта управления (классов)
Под будущими состояниями объекта управления, т.е. оросительной системы, будем понимать желательные (нормативные) и нежелательные значения МиУГВ, а также урожайность риса (табл. 1).

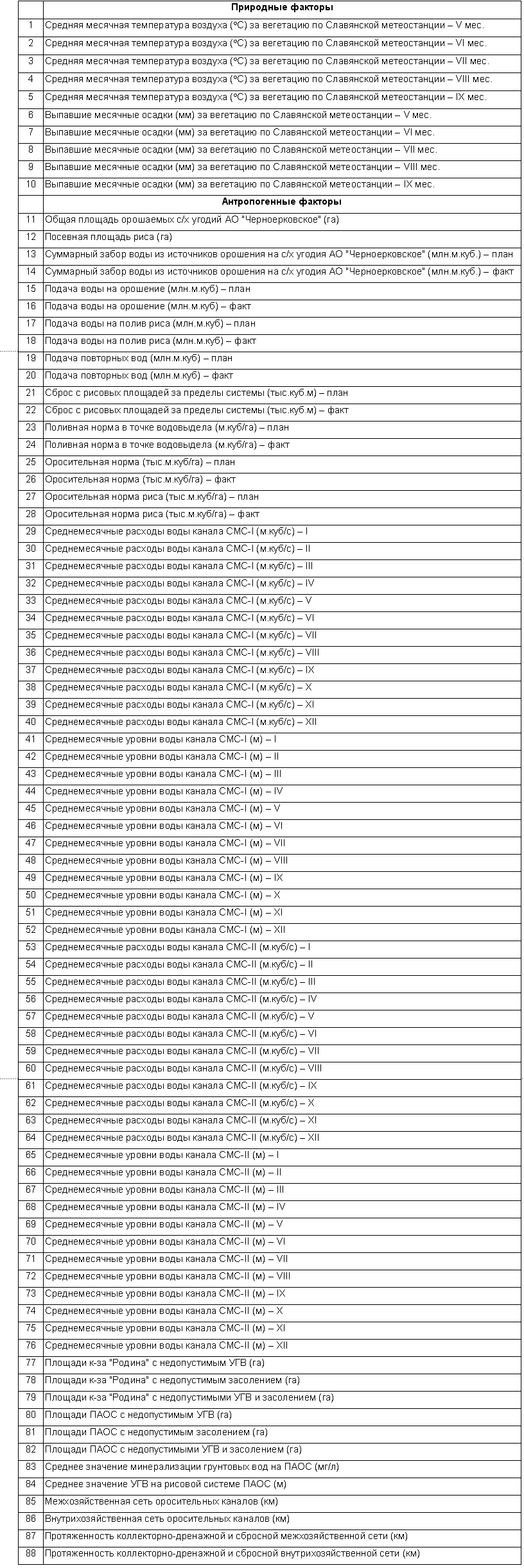
1.3. Определение природных, антропогенных и технологических факторов
Факторы, влияющие на объект управления, отнесем к двум основным группам:
1) природные факторы;
2) антропогенные факторы.
Антропогенные факторы в свою очередь разделим на следующие:
– антропогенные факторы, являющиеся побочными результатами деятельности человека;
– технологические факторы, с помощью которых специалисты осуществляют управление оросительной системой.
Все эти факторы приведены в таблице 2.
2. Формализация предметной области
2.1. Задачи формализации
Формализация предметной области осуществляется на основе ее когнитивной структуризации, проведенной в предыдущем разделе. Формализация предметной области – это конструирование классификационных и описательных шкал и градаций, как правило, порядкового типа с использованием интервальных оценок, в системе которых информация о предметной области представляется в форме, пригодной для обработки на компьютере с применением математических моделей [1].
2.2. Конструирование классификационных шкал и градаций
В соответствии с методологией СК-анализа каждый числовой фактор из таблицы 2, независимо от его смысла и единиц измерения, рассматривается как переменная числовая величина, принимающая определенное множество значений. Подобные величины формализуются путем сведения к интервальным значениям, т.е. путем введения некоторого количества диапазонов, охватывающих все множество значений фактора, и установления фактов попадания конкретного значения величины в определенный диапазон.
Для каждого фактора устанавливаются свои границы диапазонов, исходя из их количества и множества значений величины фактора.
Количество диапазонов может быть различным для разных факторов, но на практике удобнее выбирать их одинаковым. Каковы же соображения, из которых исходят при выборе количества диапазонов? Чем больше диапазонов, тем точнее интервальные оценки. Однако это происходит только тогда, когда, по крайней мере, для большинства диапазонов наблюдаются факты попадания значений факторов в них. Очевидно, для этого необходимо достаточно большое количество данных и достаточно равномерное распределение их по диапазонам. Если же данных недостаточно или они распределены по значениям очень неравномерно, то некоторые или даже многие диапазоны могут оказаться пустыми, и модель приближается к детерминистскому типу. Тогда имеет смысл уменьшить количество диапазонов, укрупнив их.
Возможен вариант сделать диапазоны различными, например, таким образом, чтобы в каждый из них попадало равное количество значений переменной. Однако этот подход в данном исследовании мы применять не будем, т.к. в этом нет необходимости.
Из этих рассуждений следует вывод, что при большом количестве данных оправданно увеличивать количество диапазонов и имеется возможность повысить точность исследования. Когда же данных недостаточно, приходится укрупнять диапазоны, что приводит к некоторой потере точности выводов, но делает их более обоснованными статистически. По-видимому, это утверждение можно считать одной из форм теоремы Котельникова об отсчетах, т.к. смысл его практически тот же самый.
СК-анализ предусматривает также возможность использования вторичных показателей, являющихся различными функциями первичных показателей. Но этот подход требует данных большего объема и за больший период времени, и поэтому в данном исследовании применяться не будет.
Основываясь на этих соображениях, мы определили количество диапазонов равным пяти.
Затем были установлены границы каждого диапазона:
– для каждого фактора были найдены минимальное и максимальное значения;
– весь интервал значений был разделен на семь равных частей.
На основе этого подхода нами предлагаются следующие классификационные и описательные шкалы и градации, в которых
– каждая классификационная шкала соответствует группе будущих состояний МиУГВ, а градации классификационных шкал – конкретным уровням минерализации и уровням грунтовых вод (табл. 3);
– каждая описательная шкала соответствует фактору, а каждая градация – определенному диапазону его изменения.

2.3. Конструирование описательных шкал и градаций
Описательные шкалы и коды градаций, сконструированные на основе подхода, изложенного в предыдущем разделе, представлены в таблице 4, а с наименованиями градаций – в таблице 5 (фрагмент).


3. Подготовка обучающей выборки
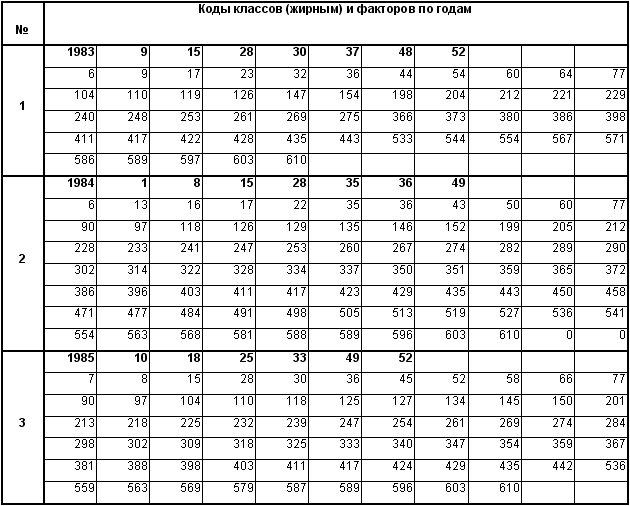
После реализации этапов конструирования классификационных и описательных шкал и градаций выполняется следующий этап: подготовка базы прецедентов (обучающей выборки). Обучающая выборка (табл. 6) представляет собой исходные данные, закодированные с использованием классификационных и описательных шкал и градаций (табл. 3–4), и состоит из двух взаимосвязанных таблиц:
– таблицы кодов классов;
– таблицы кодов градаций факторов.
Коды классов (будущих состояний МиУГВ) и градаций факторов соответствуют справочникам, представленным в таблицах 3–6.
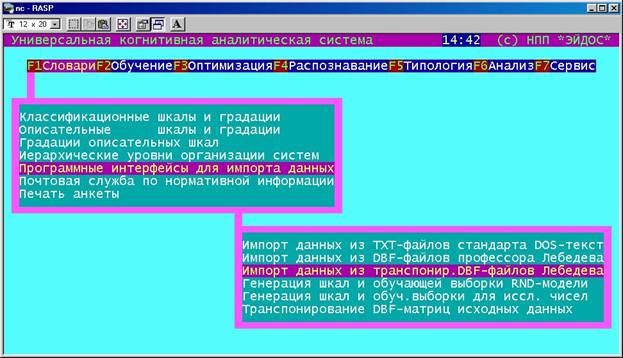
Необходимо отметить, что таблицы 3–6 формируются системой "Эйдос" автоматически в соответствии с параметрами, заданными в диалоге, в специальном режиме (см. рис.) на основе таблицы исходных данных [2], записанной из Excel в стандарте DBF 4 (dBASE IV) (*.dbf).
 |
|
Режим импорта данных из транспонированных файлов стандарта профессора А.Н.Лебедева |
Список литературы
1. Луценко Е.В. Автоматизированный системно-когнитивный анализ в управлении активными объектами (системная теория информации и ее применение в исследовании экономических, социально-психологических, технологических и организационно-технических систем): Монография (научное издание). – Краснодар: КубГАУ, 2002. – 605 с.
2. Сафронова Т.И., Луценко Е.В. Проблема управления качеством грунтовых вод на рисовых оросительных системах и концепция ее решения // Научный журнал КубГАУ. – 2004. – №5(7). – 9 с. – http://ej.kubagro.ru.
3. Пат. № 2003610986 РФ. Универсальная когнитивная аналитическая система "ЭЙДОС" / Е.В. Луценко (Россия); Заяв. № 2003610510 РФ. Опубл. от 22.04.2003. – 50 с.
4. Сафронова Т.И. Гидрогеологическое обоснование мероприятий по охране подземных вод // Труды Российской ассоциации "Женщины-математики". Воронеж, 2002. – С. 92–95.
Научный электронный журнал КубГАУ . № 05(7), 2004