|
|
Уединенные волны в физически линейных и нелинейных
вязкоупругих стержнях
Аршинов Г.А. Елисеев Н.И.
Кубанский государственный аграрный университет
Метод возмущений применяется для исследования дисперсионных волн
в геометрически нелинейных стержнях из линейно- и нелинейно-вязкоупругого
материала. Выведены эволюционное уравнение Кортевега де Вриза –
Бюргерса для линейно-вязкоупугого и модифицированное уравнение для
нелинейно-вязкоупугого стержня.
Построим одномерную модель колебаний, учитывающую в определенной
степени инерцию поперечных движений стержня. Отнесем бесконечный
стержень неизменного поперечного сечения, свободный от внешних объемных
и поверхностных воздействий, к системе координат, направив ось 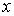 вдоль оси стержня, а оси y и вдоль оси стержня, а оси y и  расположим в одном из поперечных сечений. расположим в одном из поперечных сечений.
Аппроксимируем перемещения точек стержня функциями [1]
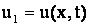 , ,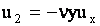 , ,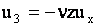 ,
(1) ,
(1)
где  – соответственно перемещения по осям x, y,
z, – соответственно перемещения по осям x, y,
z, 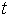 – время, – время,
 - коэффициент
Пуассона. - коэффициент
Пуассона.
Буквенные индексы, которые содержат функции (1), определяют частную
производную от функции по указанной переменной, т.е.
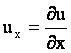 , , 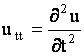 и т.д. и т.д.
Конечные деформации стержня зададим соотношениями:
 (2) (2)
где индекс после запятой определяет частную производную от функции
по соответствующей переменной, т.е. 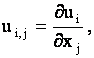
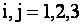 , предполагается,
что , предполагается,
что 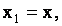 , , 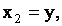 
Для описания реологических свойств стержня воспользуемся уравнениями
линейной вязкоупругости [2]
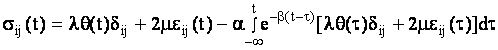 , (3) , (3)
где  - соответственно
компоненты тензоров напряжений и деформаций; - соответственно
компоненты тензоров напряжений и деформаций; 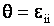 - объемное расширение,
- объемное расширение,  - символы Кронекера; - символы Кронекера; 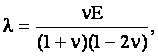 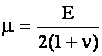 - параметры Ламе; - параметры Ламе; 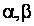 - константы, определяющие реологические
свойства стержня; Е - модуль Юнга; - константы, определяющие реологические
свойства стержня; Е - модуль Юнга;  - коэффициент Пуассона. - коэффициент Пуассона.
Для упрощения исследования заменим интегральный оператор в (3)
дифференциальным, разлагая функцию 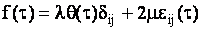 в ряд Тейлора по степеням ( в ряд Тейлора по степеням (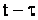 ). Ограничиваясь двумя слагаемыми, что возможно для ). Ограничиваясь двумя слагаемыми, что возможно для 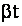 >>1,
получаем >>1,
получаем
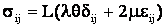 , (4) , (4)
где оператор 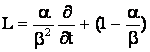 и действует на функцию и действует на функцию 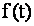 по правилу по правилу 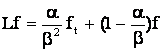 . .
Формулы (4) можно представить в развернутом виде
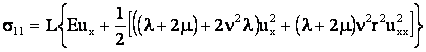
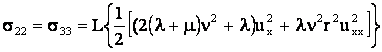
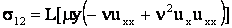
 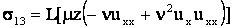
или
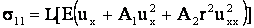
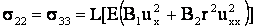
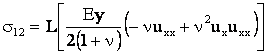
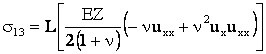 , ,
где
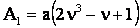 , , 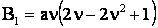 , ,
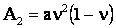 , , 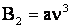 , , 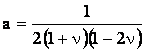 . .
Уравнение движения стержня получим из вариационного принципа 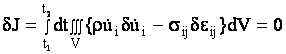 ,
(5) ,
(5)
где точкой обозначена производная по t, r - плотность материала
стержня, 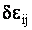 -
вариации деформаций, -
вариации деформаций, 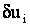 - вариации перемещений, а тройной
интеграл вычисляется по объему стержня. - вариации перемещений, а тройной
интеграл вычисляется по объему стержня.
Вычислим вариации деформаций.
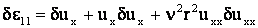
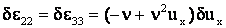
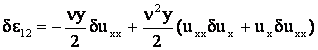
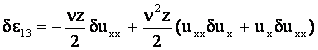
или в операторной форме
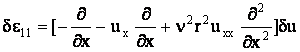

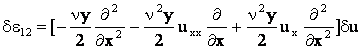
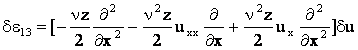 . .
Используя формулы (4) и вариации компонент деформации, определим
вариацию внутренней энергии:
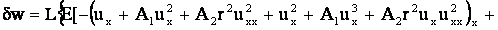
+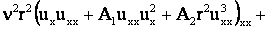

+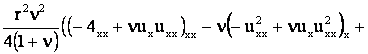
+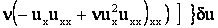

или
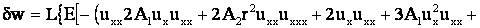
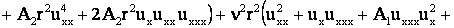
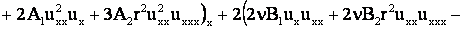
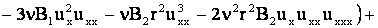
+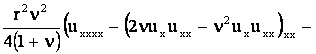  . .
Подставляя значение вариации внутренней энергии в выражение (5),
получим уравнение движения стержня:
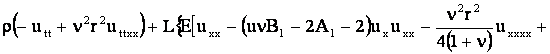
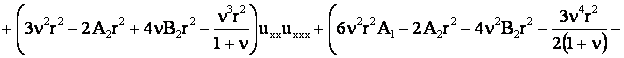
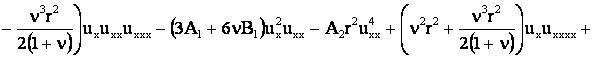
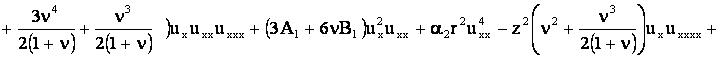

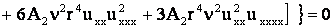 . .
После преобразования имеем:


+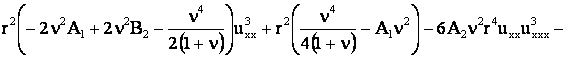
 . .
Перейдем в последнем уравнении к безразмерным переменным
 , , 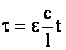 , ,
 , ,  , ,
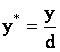 , ,
где  – амплитудный
параметр возмущения, – амплитудный
параметр возмущения, 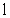 , d – соответственно характерные длина
волны и поперечный размер стержня, , d – соответственно характерные длина
волны и поперечный размер стержня, 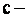 скорость волны, скорость волны, 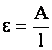 - характеристика нелинейности волнового
процесса и допустим, что - характеристика нелинейности волнового
процесса и допустим, что 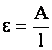 – малый параметр, т.е. характерная длина волны – малый параметр, т.е. характерная длина волны 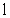 значительно превосходит амплитудный параметр
значительно превосходит амплитудный параметр  ,
а поперечные размер стержня и реологические постоянные ,
а поперечные размер стержня и реологические постоянные 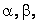 определяют отношения порядков определяют отношения порядков
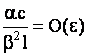 , ,  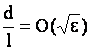 . .
Пренебрегая членами порядка выше, чем 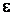 ,
получаем уравнение движения стержня: ,
получаем уравнение движения стержня:

 (6) (6)
Представим функцию  в виде асимптотического разложения в виде асимптотического разложения
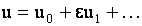 . (7) . (7)
Учитывая введенные соотношения порядков и асимптотическое разло-
жение (7), из уравнения (6) в нулевом приближении получим
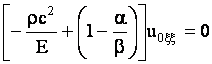 . .
Так как 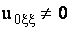 ,
то из последнего уравнения следует, что скорость распространения
волны ,
то из последнего уравнения следует, что скорость распространения
волны
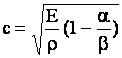 (8) (8)
Из первого приближения получаем условие разрешимости уравнения
для 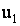 , которое
дает известное уравнение Кортевега де Вриза – Бюргерса: , которое
дает известное уравнение Кортевега де Вриза – Бюргерса:
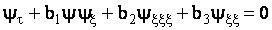 , (9) , (9)
где
 , , 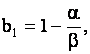 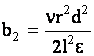 , ,
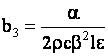 . .
Как и в линейном случае, рассмотрим бесконечный стержень неизменного
поперечного сечения, свободный от внешних объемных и поверхностных
воздействий в системе координат с осью 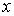 , направленной вдоль линии центров тяжести поперечных
сечений, и осями , направленной вдоль линии центров тяжести поперечных
сечений, и осями 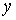 , ,  , расположенными в одном из них. , расположенными в одном из них.
Аппроксимируем перемещения точек стержня функциями (1), а конечные
деформации стержня определим формулами (2).
Для описания реологических свойств стержня в отличие от предыдущего
случая воспользуемся уравнениями квадратичной теории вязкоупругости
[2]
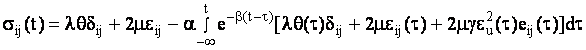 ,(10) ,(10)
где 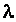 , , - параметры Ламе, - параметры Ламе, 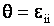 - объемное расширение, - объемное расширение,  - символы Кронекера - символы Кронекера 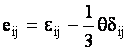 - компоненты девиатора деформаций, - компоненты девиатора деформаций,
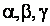 -физические константы материала, -физические константы материала, 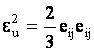 - интенсивность деформаций. - интенсивность деформаций.
Для упрощения исследования заменим интегральный оператор в уравнениях
(10) дифференциальным, разлагая функцию
 
в ряд Тейлора по степеням 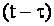 . Ограничиваясь двумя слагаемыми ряда, что возможно для . Ограничиваясь двумя слагаемыми ряда, что возможно для
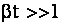 , получаем , получаем
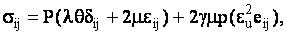
где введены операторы
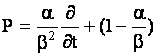 , , 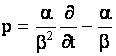 , ,
действующие на функцию 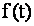 по правилу по правилу
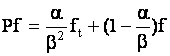 , , 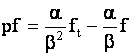 . .
Вычислим компоненты девиатора деформаций:
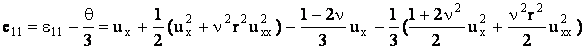
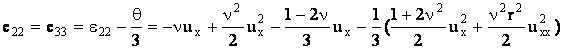
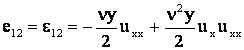
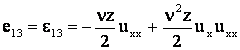 , ,
где 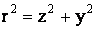
или
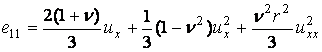
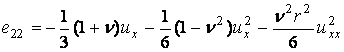
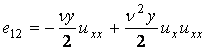
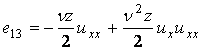 . .
Из вариационного принципа (5) получаем уравнение движения стержня,
в котором перейдем к безразмерным переменным
 , , 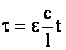 , ,
 , ,  , ,
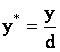 , ,
где  – амплитудный
параметр возмущения, – амплитудный
параметр возмущения, 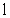 , d – соответственно характерные длина
волны и поперечный размер стержня, , d – соответственно характерные длина
волны и поперечный размер стержня, 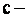 скорость волны, скорость волны, 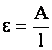 - характеристика нелинейности волнового
процесса. - характеристика нелинейности волнового
процесса.
Допустим, что 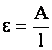 – малый параметр, т.е. характерная длина волны
– малый параметр, т.е. характерная длина волны
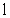 значительно
превосходит амплитудный параметр значительно
превосходит амплитудный параметр  ,
а поперечные размер стержня и реологические постоянные ,
а поперечные размер стержня и реологические постоянные 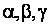 определяют отношения порядков определяют отношения порядков
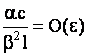 , , 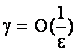 , , 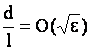 , ,
где 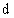 - характерный
размер поперечного сечения. - характерный
размер поперечного сечения.
Опуская звездочки в выражениях для соответствующих безразмерных
переменных, получим уравнение движения

+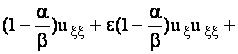 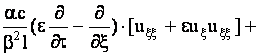 (11) (11)
+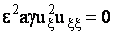 , ,
где  . .
Представим функцию 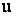 асимптотическим разложением асимптотическим разложением 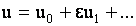 .
Подставляя это разложение в уравнение движения (11) и учитывая введенные
отношения порядков, в нулевом приближении приходим к уравнению .
Подставляя это разложение в уравнение движения (11) и учитывая введенные
отношения порядков, в нулевом приближении приходим к уравнению
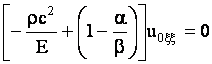 , ,
где 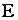 - модуль упругости. Так как - модуль упругости. Так как 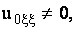 то из полученного уравнения скорость распространения
возмущения то из полученного уравнения скорость распространения
возмущения 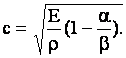
Первое приближение дает модифицированное уравнение Кортевега де
Вриза – Бюргерса
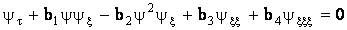 (12) (12)
где 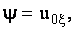  , ,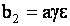 , , 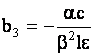 , , 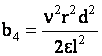 . .
Список литературы
1.Аршинов Г.А., Могилевич Л.И. Статические и динамические задачи
вязкоупругости. Саратов: Изд-во СГАУ, 2002. 152 с.
|

