Научный электронный журнал КубГАУ . № 03(19), 2006
УДК 330.142.211
ОЦЕНКА РИСКА ИНВЕСТИЦИОННОГО ПРОЕКТА
Попова А. Ю. – ассистент
Адыгейский государственный университет
В статье рассматривается проблема учета риска и неопределенности при принятии решения об инвестировании. При этом проводится подробный сравнительный анализ существующих методов оценки риска инвестиционных проектов, а также рассматриваются возможные пути преодоления их недостатков.
It is considered in this article the problem of risk and vagueness calculation by taking a decision of investing. For this it is carried out the detailed comparative analysis of existing methods of invest projects risk and possible ways of overcoming of their deficiencies are examined.
Необходимым условием стабильного функционирования и развития экономики является эффективная инвестиционная политика, ведущая к увеличению объемов производства, росту национального дохода, развитию различных отраслей и предприятий.
Но, анализируя эффективность тех или иных инвестиционных проектов, часто приходится сталкиваться с тем, что рассматриваемые при их оценке потоки денежных средств (расходы и доходы) относятся к будущим периодам и носят прогнозный характер. Неопределенность будущих результатов обусловлена влиянием как множества экономических факторов (колебания рыночной конъюнктуры, цен, валютных курсов, уровня инфляции и т. п.), не зависящих от усилий инвесторов, так и достаточного числа неэкономических факторов (климатические и природные условия, политические отношения и т. д.), которые не всегда поддаются точной оценке.
Неопределенность прогнозируемых результатов приводит к возникновению риска того, что цели, поставленные в проекте, могут быть не достигнуты полностью или частично.
В настоящее время существует большое число различных определений самих понятий "риск" и "неопределенность".
В экономической практике обычно не делают различия между риском и неопределенностью. При этом под термином "риск" понимают некоторую возможную потерю, вызванную наступлением случайных неблагоприятных событий [22].
В ряде случаев под рискованностью инвестиционного проекта понимается возможность отклонения будущих денежных потоков по проекту от ожидаемого потока. Чем больше отклонение, тем более рискованным считается проект [21].
Однако еще в первом в экономике научном определении риска Ф. Найтом было предложено различать понятия "риск" и "неопределенность". Риск имеет место тогда, когда некоторое действие может привести к нескольким взаимоисключающим исходам с известным распределением их вероятностей. Если же такое распределение неизвестно, то соответствующая ситуация рассматривается как неопределенность [6; 22].
В настоящее время многие авторы определяют риск как производную от факторов неопределенности [2; 8; 10; 16; 17; 19]. При этом под неопределенностью понимается неполнота или неточность информации об условиях реализации проекта, в том числе о связанных с ними затратах и результатах. Неопределенность, связанная с возможностью возникновения в ходе реализации проекта неблагоприятных ситуаций и последствий, характеризуется понятием риска.
Альтернативной является трактовка риска как возможности любых (позитивных или негативных) отклонений показателей от предусмотренных проектом их средних значений [17].
В вопросе об оценке риска инвестиционного проекта также нет методологической однозначности. Хотя большинство авторов, занимающихся вопросами инвестирования, обычно выделяют два основных подхода (качественный и количественный), тем не менее имеются существенные расхождения при рассмотрении конкретных методов оценки.
Главная задача качественного подхода состоит в выявлении и идентификации возможных видов рисков рассматриваемого инвестиционного проекта, а также в определении и описании источников и факторов, влияющих на данный вид риска. Кроме того, качественный анализ предполагает описание возможного ущерба, его стоимостной оценки и мер по снижению или предотвращению риска (диверсификация, страхование рисков, создание резервов и т. д.).
Качественный подход, не позволяющий определить численную величину риска инвестиционного проекта, является основой для проведения дальнейших исследований с помощью количественных методов, широко использующих математический аппарат теории вероятностей, математической статистики, теории исследования операций.
Основная задача количественного подхода заключается в численном измерении влияния факторов риска на поведение критериев эффективности инвестиционного проекта.
Среди качественных методов оценки инвестиционного риска наиболее часто используются следующие:
- анализ уместности затрат;
- метод аналогий;
- метод экспертных оценок.
Основой анализа уместности затрат [6; 10] выступает предположение о том, что перерасход средств может быть вызван одним или несколькими из следующих факторов:
- изначальная недооценка стоимости проекта в целом или его отдельных фаз и составляющих;
- изменение границ проектирования, обусловленное непредвиденными обстоятельствами;
- отличие производительности машин и механизмов от предусмотренной проектом;
- увеличение стоимости проекта в сравнении с первоначальной вследствие инфляции или изменения налогового законодательства.
В процессе анализа, исходя из условий конкретного инвестиционного проекта, происходит детализация указанных факторов и составляется контрольный перечень возможного повышения затрат по статьям для каждого варианта проекта или его элементов.
Процесс финансирования разбивается на стадии, связанные с фазами реализации проекта. При этом необходимо также учитывать и дополнительную информацию о проекте, поступающую по мере его разработки. Поэтапное выделение средств позволяет инвестору при первых признаках того, что риск вложения растет, или прекратить финансирование проекта, или же начать поиск мер, обеспечивающих снижение затрат.
Не менее распространенным при проведении качественной оценки инвестиционного риска является метод аналогий [6; 9; 10]. Суть его заключается в анализе всех имеющихся данных по не менее рискованным аналогичным проектам, изучении последствий воздействия на них неблагоприятных факторов с целью определения потенциального риска при реализации нового проекта.
При этом источником информации могут служить регулярно публикуемые западными страховыми компаниями рейтинги надежности проектных, подрядных, инвестиционных и прочих компаний, анализы тенденций изменения спроса на конкретную продукцию, цен на сырье, топливо, землю и т. д. В настоящее время и российские проектные организации стали создавать базы данных о рискованных проектах путем изучения литературных источников, проведения исследовательских работ и опроса менеджеров проектов.
Основная сложность при использовании данного метода состоит в правильном подборе аналога, т. к. отсутствуют формальные критерии, позволяющие установить степень аналогичности ситуаций. Но даже если удается подобрать аналог, то, как правило, очень трудно сформулировать предпосылки для анализа, исчерпывающий и реалистический набор возможных сценариев срыва проекта. Причина состоит в том, что большинство подобных ситуаций качественно различны, возникающие осложнения нередко наслаиваются друг на друга, а их эффект проявляется как результат сложного взаимодействия.
Также крайне затруднительно оценить степень точности, с которой уровень риска аналогичного проекта можно принять за риск рассматриваемого. Более того, отсутствуют методические разработки, подробно описывающие логику и детали подобной процедуры оценивания риска [9].
Все вышесказанное свидетельствует о том, что метод анализа уместности затрат и метод аналогий пригодны скорее для описания возможных рисковых ситуации, нежели для получения более или менее точной оценки риска инвестиционного проекта.
Метод экспертных оценок [6; 7; 9] базируется на опыте экспертов в вопросах управления инвестиционными проектами. Анализ начинается с составления исчерпывающего перечня рисков по всем стадиям проекта. Каждому эксперту, работающему отдельно, предоставляется перечень первичных рисков в виде опросных листов и предлагается оценить вероятность их наступления, руководствуясь специальной системой оценок. В том случае, если между мнениями экспертов будут обнаружены большие расхождения, они обсуждаются всеми экспертами для выработки более согласованной позиции. В целях получения более объективной оценки специалисты, проводящие экспертизу, должны обладать полным спектром информации об оцениваемом проекте.
После определения вероятностей по простым рискам возникает вопрос о выборе метода сведения разнообразных показателей к единой интегральной оценке. В качестве такого метода обычно используется один из традиционных методов получения рейтинговых показателей, например, взвешивание. Этот метод предполагает определение весовых коэффициентов, с которыми каждый простой риск входит в общий риск проекта. При этом нет никакой необходимости использовать для каждой группы рисков единую систему весов, единообразный подход должен соблюдаться только внутри каждой отдельно взятой группы. Важно лишь, чтобы соблюдались такие общие требования, как неотрицательность весовых коэффициентов и приравнивание их суммы к единице.
Наибольшего внимания
заслуживает подход, предполагающий ранжирование отдельных рисков по степени
приоритетности и определение весовых коэффициентов k в соответствии со
значимостью этих рисков. Так, максимальное значение весового коэффициента ![]() присваивается рискам,
имеющим в сложившейся ситуации первостепенное значение, минимальное
присваивается рискам,
имеющим в сложившейся ситуации первостепенное значение, минимальное ![]() – рискам последнего
ранга. Риски с равной значимостью получают одинаковые весовые коэффициенты.
Определяется также значение соотношения между весовыми коэффициентами первого и
последнего рангов (
– рискам последнего
ранга. Риски с равной значимостью получают одинаковые весовые коэффициенты.
Определяется также значение соотношения между весовыми коэффициентами первого и
последнего рангов (![]() ).
).
В качестве способа взвешивания используется расчет средней арифметической (веса, соответствующие соседним рангам, отличаются на одну и ту же величину) или средней геометрической (веса, соответствующие соседним рангам, различаются в одинаковое число раз).
Расстояние между
соседними рангами можно исчислить по формуле (для средней арифметической): ![]() .
.
Весовой коэффициент
отдельного риска с рангом m составляет ![]() .
.
Отсюда ![]() .
.
Если простые риски не
ранжируются по степени приоритетности, то они, соответственно, имеют весовые
коэффициенты ![]() .
.
Основная проблема, возникающая при использовании метода экспертных оценок, связана с объективностью и точностью получаемых результатов. Это связано с такими факторами, как некачественный подбор экспертов, возможность группового обсуждения, доминирование какого-либо мнения (мнения "авторитетного лидера") и т. д.
Наибольшее распространение при оценке риска инвестиционных проектов (особенно производственных инвестиций) получили такие количественные методы, как:
- статистический метод;
- анализ чувствительности (метод вариации параметров);
- метод проверки устойчивости (расчета критических точек);
- метод сценариев (метод формализованного описания неопределенностей);
- имитационное моделирование (метод статистических испытаний, метод Монте-Карло);
- метод корректировки ставки дисконтирования.
Часто производственная деятельность предприятий планируется по средним показателям параметров, которые заранее не известны достоверно (например, прибыль) и могут меняться случайным образом. При этом крайне нежелательна ситуация с резкими изменениями этих показателей, ведь это означает угрозу утери контроля. Чем меньше отклонение показателей от среднего ожидаемого значения, тем больше стабильность рыночной обстановки.
Именно поэтому наибольшее распространение при оценке инвестиционного риска получил статистический метод, основанный на методах математической статистики [3; 7; 9; 10; 11; 12; 20; 21].
Расчет среднего ожидаемого значения осуществляется по формуле средней арифметической взвешенной:
![]() , где
, где ![]() – среднее ожидаемое значение;
– среднее ожидаемое значение; ![]() – ожидаемое значение для
каждого случая;
– ожидаемое значение для
каждого случая; ![]() –
число случаев наблюдения (частота).
–
число случаев наблюдения (частота).
Среднее ожидаемое значение представляет собой обобщенную количественную характеристику и поэтому не позволяет принять решение в пользу какого-либо варианта инвестирования.
Для принятия окончательного решения необходимо определить меру колеблемости возможного результата. Колеблемость представляет собой степень отклонения ожидаемого значения от среднего. Для ее оценки на практике обычно применяют два близко связанных критерия – дисперсию и среднее квадратичное отклонение.
Дисперсия есть средневзвешенное значение квадратов отклонений действительных результатов от средних ожидаемых:
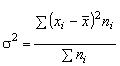 .
.
Среднее квадратичное отклонение определяется по формуле:
 .
.
Среднее квадратичное отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратичное отклонение являются мерами абсолютной колеблемости.
Для анализа результатов и затрат, предусматриваемых инвестиционным проектом, как правило, используют коэффициент вариации. Он представляет собой отношение среднего квадратичного отклонения к средней арифметической и показывает степень отклонения полученных значений:
![]() (в процентах).
(в процентах).
Коэффициент может изменяться от 0 до 100 %. Чем больше коэффициент, тем сильнее колеблемость. Принята следующая качественная оценка различных значений коэффициента вариации: до 10 % – слабая колеблемость, 10–25 % – умеренная, свыше 25 % – высокая.
При одинаковых значениях уровня ожидаемого дохода более надежными являются вложения, которые характеризуются меньшим значением среднеквадратического отклонения, показывающего колеблемость вероятности получения ожидаемого дохода (вариацию доходности).
При различии значений средних уровней доходности по сравниваемым инвестиционным объектам выбор направления вложений исходя из значений вариации невозможен, поэтому в данных случаях инвестиционное решение принимается на основе коэффициента вариации, оценивающего размер риска на величину доходности. Предпочтение отдается тем инвестиционным проектам, по которым значение коэффициента является более низким, что свидетельствует о лучшем соотношении дохода и риска.
Основным преимуществом статистического метода является то, что он позволяет оценивать риск не только рассматриваемого инвестиционного проекта, но и всего предприятия в целом, анализируя динамику его доходов за определенный отрезок времени. Несмотря на несложность выполнения математических расчетов, для использования данного метода необходимо большое количество информации и данных за длительный период времени, что и является его основным недостатком.
Кроме того, описанные выше характеристики предполагается применять к нормальному закону распределения вероятностей. Он, действительно, широко используется при анализе рисков, т. к. его важнейшие свойства (симметричность распределения относительно средней, ничтожная вероятность больших отклонений случайной величины от центра ее распределения, правило трех сигм) позволяют существенно упростить анализ. Однако не всегда при анализе инвестиций доходы подчиняются нормальному закону.
В подобных случаях использование в процессе анализа только вышеперечисленных характеристик может приводить к неверным выводам. Поэтому необходимо использование дополнительных параметров, таких, например, как коэффициент асимметрии (скоса), эксцесс и т. д.
Также следует отметить, что применение более сложного аппарата математической статистики (регрессионного и корреляционного анализа, методов имитационного моделирования) позволило бы провести более глубокий анализ риска и причин его возникновения [9].
В инвестиционном проектировании при оценке риска применяется также анализ чувствительности [2; 5; 9; 10; 13; 17; 19; 20; 21]. При использовании данного метода риск рассматривается как степень чувствительности результирующих показателей реализации проекта к изменению условий функционирования (изменение налоговых платежей, ценовые изменения, изменения средних переменных издержек и т. п.). В качестве результирующих показателей реализации проекта могут выступать: показатели эффективности (NPV, IRR, PI, срок окупаемости); ежегодные показатели проекта (чистая прибыль, накопленная прибыль).
Анализ начинается с установления базового значения результирующего показателя (например, NPV) при фиксированных значениях параметров, влияющих на результат оценки проекта. Затем рассчитывается процентное изменение результата (NPV) при изменении одного из условий функционирования (другие факторы предполагаются неизменными). Как правило, границы вариации параметров составляют + - 10–15 %.
Наиболее информативным методом, применяемым для анализа чувствительности, является расчет показателя эластичности, представляющего собой отношение процентного изменения результирующего показателя к изменению значения параметра на один процент.
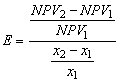 , где
, где ![]() – базовое значение варьируемого параметра,
– базовое значение варьируемого параметра, ![]() – измененное значение
варьируемого параметра,
– измененное значение
варьируемого параметра, ![]() –
значение результирующего показателя для базового варианта,
–
значение результирующего показателя для базового варианта, ![]() – значение результирующего
показателя при изменении параметра.
– значение результирующего
показателя при изменении параметра.
Таким же образом исчисляются показатели чувствительности по каждому из остальных параметров.
Чем выше значения показателя эластичности, тем чувствительнее проект к изменениям данного фактора, и тем сильнее подвержен проект соответствующему риску.
Анализ чувствительности можно также проводить и графически, путем построения прямой реагирования значения результирующего показателя (NPV) на изменение данного фактора. Чем больше угол наклона этой прямой, тем чувствительнее значение NPV к изменению параметра и больше риск.
Пересечение прямой реагирования с осью абсцисс показывает, при каком изменении (рост – со знаком плюс, снижение – со знаком минус) параметра в процентном выражении проект станет неэффективным.
Затем на основании этих расчетов происходит экспертное ранжирование параметров по степени важности (например, очень высокая, средняя, невысокая) и построение так называемой "матрицы чувствительности", позволяющей выделить наименее и наиболее рискованные для проекта факторы.
Анализ чувствительности позволяет определить ключевые (с точки зрения устойчивости проекта) параметры исходных данных, а также рассчитать их критические (предельно допустимые) значения.
Как видно, анализ чувствительности до некоторой степени является экспертным (качественным) методом. Кроме того, главным недостатком данного метода является предпосылка того, что изменение одного фактора рассматривается изолированно, тогда как на практике все экономические факторы в той или иной степени коррелированны.
По этой причине применение данного метода как самостоятельного инструмента анализа риска на практике, по мнению ряда авторов, весьма ограничено, если вообще возможно.
Метод проверки устойчивости [3; 6; 8; 9; 10; 13; 16; 17; 19; 20] предусматривает разработку сценариев реализации проекта в наиболее вероятных или наиболее "опасных" для каких-либо участников условиях. По каждому сценарию исследуется, как будет действовать в соответствующих условиях организационно-экономический механизм реализации проекта, каковы будут при этом доходы, потери и показатели эффективности у отдельных участников, государства и населения. Влияние факторов риска на норму дисконта при этом не учитывается.
Проект считается устойчивым и эффективным, если во всех рассмотренных ситуациях
- NPV положителен;
- обеспечивается необходимый резерв финансовой реализуемости проекта.
Степень устойчивости проекта по отношению к возможным изменениям условий реализации может быть охарактеризована показателями предельного (критического) уровня объемов производства, цен производимой продукции и других параметров проекта.
Предельное значение параметра проекта для некоторого t-го года его реализации определяется как такое значение этого параметра в t-ом году, при котором чистая прибыль участника в этом году становится нулевой. Одним из наиболее важных показателей этого типа является точка безубыточности, характеризующая объем продаж, при котором выручка от реализации продукции совпадает с издержками производства:
![]() , где
, где ![]() - постоянные
затраты, уровень которых напрямую не связан с объемом производства продукции;
- постоянные
затраты, уровень которых напрямую не связан с объемом производства продукции; ![]() – переменные затраты,
величина которых изменяется с изменением объема производства продукции;
– переменные затраты,
величина которых изменяется с изменением объема производства продукции; ![]() – цена единицы продукции.
– цена единицы продукции.
Ограничения, которые должны соблюдаться при расчете точки безубыточности:
- объем производства равен объему продаж;
- постоянные затраты одинаковы для любого объема;
- переменные издержки изменяются пропорционально объему производства;
- цена не изменяется в течение периода, для которого определяется точка безубыточности;
- цена единицы продукции и стоимость единицы ресурсов остаются постоянными;
- в случае расчета точки безубыточности для нескольких наименований продукции соотношение между объемами производимой продукции должно оставаться неизменным.
Для подтверждения работоспособности проектируемого производства (на данном шаге расчета) необходимо, чтобы значение точки безубыточности было меньше значений номинальных объемов производства и продаж (на этом шаге). Чем дальше от них значение точки безубыточности (в процентном отношении), тем устойчивее проект.
Обычно проект считается устойчивым, если в расчетах по проекту в целом значение точки безубыточности не превышает 60–70 % от номинального объема производства после освоения проектных мощностей. Близость значения точки безубыточности к 100 %, как правило, свидетельствует о недостаточной устойчивости проекта к колебаниям спроса на продукцию на данном шаге.
Но даже удовлетворительные значения точки безубыточности на каждом шаге не гарантируют эффективность проекта (положительность NPV), т. к. при определении точки безубыточности в величине издержек обычно не включаются выплаты на компенсацию инвестиционных затрат, процентов по кредитам и т. д. В то же время высокие значения точки безубыточности на отдельных шагах не могут рассматриваться как признак нереализуемости проекта (например, на этапе освоения вводимых мощностей или в период капитального ремонта дорогостоящего высокопроизводительного оборудования они могут превышать 100 %).
Кроме того, данный метод не дает возможности провести комплексный анализ риска по всем взаимосвязанным параметрам, т. к. каждый показатель предельного уровня характеризует степень устойчивости в зависимости лишь от конкретного параметра проекта (объем производства и т. д.).
В какой-то мере избежать недостатков, присущих анализу чувствительности, позволяет метод сценариев, при котором одновременному непротиворечивому изменению подвергается вся совокупность факторов исследуемого проекта с учетом их взаимозависимости [2; 5; 8; 10; 13; 16; 17; 19; 20].
Метод сценариев предполагает описание опытными экспертами всего множества возможных условий реализации проекта (либо в форме сценариев, либо в виде системы ограничений на значения основных технических, экономических и прочих параметров проекта) и отвечающих этим условиям затрат, результатов и показателей эффективности.
В качестве возможных вариантов целесообразно построить как минимум три сценария: пессимистический, оптимистический и наиболее вероятный (реалистический, или средний).
Следующий этап реализации метода сценариев состоит в преобразовании исходной информации о факторах неопределенности в информацию о вероятностях отдельных условий реализации и соответствующих показателях эффективности или об интервалах их изменения.
На основе имеющихся данных определяются показатели экономической эффективности проекта.
Если вероятности наступления того или иного события, отраженного в сценарии, известны точно (вероятностная неопределенность), то ожидаемый интегральный эффект проекта рассчитывается по формуле математического ожидания:
![]() , где
, где ![]() – интегральный эффект при условии реализации i-ого сценария,
– интегральный эффект при условии реализации i-ого сценария, ![]() – вероятность этого
сценария.
– вероятность этого
сценария.
При этом риск
неэффективности проекта (![]() ) оценивается как суммарная вероятность тех
сценариев (к), при которых ожидаемая эффективность проекта (
) оценивается как суммарная вероятность тех
сценариев (к), при которых ожидаемая эффективность проекта (![]() ) становится отрицательной.
) становится отрицательной.
![]() .
.
Средний ущерб от
реализации проекта в случае его неэффективности (![]() ) определяется по формуле:
) определяется по формуле:
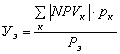 .
.
Вероятностное описание условий реализации проекта оправдано и применимо, когда эффективность проекта обусловлена прежде всего неопределенностью природно-климатических условий (погода, характеристики грунта или запасов полезных ископаемых, возможность землетрясений или наводнений и т. п.) или процессов эксплуатации и износа основных средств (снижение прочности конструкций зданий и сооружений, отказы оборудования и т. п.).
В тех случаях, когда ничего не известно о вероятности отдельных сценариев (интервальная неопределенность) или реализация любого из них вообще не является случайным событием и не может быть охарактеризована в терминах теории вероятности, используется минимаксный подход, в частности, так называемый критерий оптимизма-пессимизма, предложенный Л. Гурвицем:
![]() , где
, где ![]() – наибольший и наименьший
интегральный эффект по рассмотренным сценариям;
– наибольший и наименьший
интегральный эффект по рассмотренным сценариям; ![]() – специальный норматив для учета
неопределенности эффекта, отражающий систему предпочтений соответствующего
хозяйственного субъекта в условиях неопределенности (рекомендуется принимать на
уровне 0,3).
– специальный норматив для учета
неопределенности эффекта, отражающий систему предпочтений соответствующего
хозяйственного субъекта в условиях неопределенности (рекомендуется принимать на
уровне 0,3).
При ![]() критерий обращается в критерий
Вальда, требующий оценивать эффективность проекта пессимистически, применительно
к худшему из возможных сценариев.
критерий обращается в критерий
Вальда, требующий оценивать эффективность проекта пессимистически, применительно
к худшему из возможных сценариев.
Однако следует отметить, что стремление минимизировать риски, настраиваясь на наихудший сценарий, может привести к неоправданно высоким затратам и созданию слишком больших резервов в случае реализации более благоприятной ситуации. Кроме того, возможно, что многие успешные проекты в этом случае будут отклонены.
При ![]() критерий Гурвица обращается в
критерий крайнего оптимизма, ориентирующийся на наилучший из возможных
сценариев, хотя вероятность его реализации обычно не очень высока.
критерий Гурвица обращается в
критерий крайнего оптимизма, ориентирующийся на наилучший из возможных
сценариев, хотя вероятность его реализации обычно не очень высока.
Основным недостатком сценарного анализа является рассмотрение только нескольких возможных исходов по проекту (дискретное множество значений NPV), хотя в действительности число возможных исходов не ограничено. Кроме того, при невозможности использования объективного метода определения вероятности того или иного сценария приходится делать предположения, основываясь на личном опыте или суждении, при этом возникает проблема достоверности вероятностных оценок.
При применении
минимаксного подхода, хотя и не использующего вероятности отдельных сценариев,
большой субъективностью отличается выбор специального норматива ![]() .
.
Как вспомогательный инструмент при проведении сценарного анализа удобно использовать метод дерева решений [3; 5; 20; 21]. Он применяется в тех ситуациях, когда решения, принимаемые в каждый момент времени, сильно зависят от предыдущих решений и в свою очередь определяют сценарии дальнейшего развития событий.
Дерево решений – это сетевые графики, каждая ветвь которых представляет собой альтернативные варианты развития или состояния среды.
При проведении сценарного анализа на сетевом графике указываются вероятности наступления тех или иных событий, а затем производится расчет ожидаемых результатов.
Ограничением практического использования данного метода является исходная предпосылка, что проект должен иметь обозримое или разумное число вариантов развития.
Анализ рисков с использованием метода имитационного моделирования (метода Монте-Карло) представляет собой соединение методов анализа чувствительности и анализа сценариев на базе теории вероятности [2; 3; 5; 10; 15; 20; 21]. Вместо того чтобы создавать отдельные сценарии (наилучший, наихудший), в имитационном методе компьютер генерирует сотни возможных комбинаций параметров (факторов) проекта с учетом их вероятностного распределения. Каждая комбинация дает свое значение NPV, и в совокупности аналитик получает вероятностное распределение возможных результатов проекта. Реализация этой достаточно сложной методики возможна только с помощью современных информационных технологий.
Имитационное моделирование строится по следующей схеме:
- формулируются параметры (факторы), влияющие на денежные потоки проекта;
- строится вероятностное распределение по каждому параметру (фактору);
Как правило, предполагается, что функция распределения является нормальной, следовательно, для того чтобы задать ее, необходимо определить только два момента (математическое ожидание и дисперсию):
- компьютер случайным образом выбирает значение каждого фактора риска, основываясь на его вероятностном распределении;
- эти значения факторов риска комбинируются с параметрами (факторами), по которым не ожидается изменение (например, налоговая ставка или норма амортизации), и рассчитывается значение чистого денежного потока для каждого года. По чистым денежным потокам рассчитывается значение чистого дисконтированного дохода (NPV);
- описанные выше действия повторяются много раз (обычно около 500 имитаций), что позволяет построить вероятностное распределение NPV;
- результаты имитации дополняются вероятностным и статистическим анализом.
Метод Монте-Карло является мощным средством анализа инвестиционных рисков, позволяя учитывать максимально возможное число факторов внешней среды. Необходимость его применения в отечественной финансовой практике обусловлена особенностями российского рынка, характеризующегося субъективизмом, зависимостью от внеэкономических факторов и высокой степенью неопределенности.
Но тем не менее этот подход не лишен недостатков:
- существование коррелированных параметров сильно усложняет модель, оценка их зависимости не всегда доступна аналитикам;
- иногда трудно даже приблизительно определить для исследуемого параметра (фактора) или результирующего показателя вид вероятностного распределения;
- при разработке реальных моделей может возникнуть необходимость привлечения специалистов или научных консультантов со стороны;
- исследование модели возможно только при наличии вычислительной техники и специальных пакетов прикладных программ;
- следует также отметить относительную неточность полученных результатов по сравнению с другими методами численного анализа.
В зависимости от того, каким методом учитывается неопределенность условий реализации проекта при определении ожидаемого NPV, поправка на риск в расчетах эффективности может включаться либо в норму дисконта (метод корректировки ставки дисконтирования) [17], либо в величину чистого гарантированного денежного потока (метод эквивалентного денежного потока) [21].
Норма дисконта, не включающая премии за риск (безрисковая норма дисконта), отражает доходность альтернативных безрисковых направлений инвестирования. Ее рекомендуется определять в следующем порядке.
При оценке коммерческой эффективности проекта в целом безрисковая коммерческая норма дисконта может устанавливаться в соответствии с требованиями к минимально допустимой будущей доходности вкладываемых средств, определяемой в зависимости от депозитных ставок банков первой категории надежности (после исключения инфляции), а также (в перспективе) ставки LIBOR по годовым еврокредитам, освобожденной от инфляционной составляющей, практически 4–6 %.
Безрисковая норма дисконта, используемая для оценки эффективности участия предприятия в проекте, назначается инвестором самостоятельно. При этом рекомендуется ориентироваться:
- на скорректированную на годовой темп инфляции рыночную ставку доходности по долгосрочным (не менее 2 лет) государственным облигациям;
- на скорректированную на годовой темп инфляции доходность вложений в операции на открытых для импорта конкурентных рынках относительно безрисковых товаров и услуг (продовольственных и лекарственных товаров первой необходимости, горюче-смазочных материалов и т. д.).
Безрисковая социальная (общественная) норма дисконта, используемая для оценки общественной и региональной эффективности, считается национальным параметром и должна устанавливаться централизованно органами управления экономикой народного хозяйства России в увязке с прогнозами экономического и социального развития страны.
Норма дисконта, включающая поправку на риск, отражает доходность альтернативных направлений инвестирования, характеризующихся тем же риском, что и инвестиции в оцениваемый проект.
При этом в величине поправки на риск обычно учитываются три типа рисков, связанных с реализацией инвестиционного проекта:
- страновой риск;
- риск ненадежности участников проекта;
- риск неполучения предусмотренных проектом доходов.
Поправка на каждый вид риска не вводится, если инвестиции застрахованы на соответствующий страховой случай.
Величина поправки на страновой риск оценивается экспертно:
- по зарубежным странам на основании рейтингов стран мира по уровню странового риска инвестирования, публикуемых специализированной рейтинговой фирмой ВЕRI (Германия), Ассоциацией швейцарских банков, аудиторской корпорацией "Ernst@Young";
- по России страновой риск определяется по отношению к безрисковой, безынфляционной норме дисконта и может превышать ее в несколько (2, 3 и более) раз. При этом размер поправки на страновой риск снижается в условиях предоставления проекту федеральной (и в меньшей степени региональной) поддержки, а также когда проект реализуется на условиях соглашения о разделе продукции.
Размер премии за риск ненадежности участников проекта определяется экспертно каждым конкретным участником проекта. Обычно поправка на этот вид риска не превышает 5 %, однако ее величина существенно зависит от того, насколько детально проработан организационно-экономический механизм реализации проекта, насколько учтены в нем опасения участников проекта.
Поправка на риск неполучения предусмотренных проектом доходов определяется с учетом технической реализуемости и обоснованности проекта, детальности проработки проектных решений, наличия необходимого научного и опытно-конструкторского задела и представительности маркетинговых исследований.
При этом если отсутствуют специальные соображения относительно рисков инвестиционного проекта, размер этого вида поправки на риск рекомендуется ориентировочно определять в соответствии с таблицей. Однако в отдельных отраслях поправки на риск могут отличаться от указанных в этой таблице.

Поправка на риск помимо вышеизложенного метода может быть определена пофакторным расчетом. При этом в поправке на риск суммируется влияние учитываемых факторов. К числу этих факторов можно отнести:
- новизну применяемой технологии;
- степень неопределенности объемов спроса и уровня цен на производимую продукцию;
- наличие нестабильности (цикличности) спроса на продукцию;
- наличие неопределенности внешней среды при реализации проекта;
- наличие неопределенности процесса освоения применяемой техники или технологии.
Каждому фактору в зависимости от его оценки можно приписать величину поправки на риск по этому фактору, зависящую от отрасли, к которой относится проект, и региона, в котором он реализуется. В тех случаях, когда эти факторы являются независимыми и в смысле риска дополняют друг друга, поправки на риск по отдельным факторам следует сложить для получения общей поправки, учитывающей риск неполучения доходов, запланированных проектом.
Однако следует отметить, что расчет, основанный на поправке к норме дисконта, одинаковой для положительных и отрицательных элементов денежного потока (хотя, возможно, и переменной во времени), может приводить к неоправданному завышению эффективности как всего проекта (для проектов, денежные потоки которых принимают отрицательные значения не только в начале расчетного периода), так и эффективности участия в проекте.
Кроме того, указанный подход расчета нормы дисконта с поправкой на риск обладает определенной долей субъективизма и не учитывает корреляцию факторов. Попыткой избежать этого является подход, который основывается на интерпретации поправки на риск как характеристики случайной величины, а именно премий за риск конкретных инвестиций в исследуемой области бизнеса. При этом предполагается, что премия за риск как случайная величина имеет нормальный закон распределения [1].
Из сказанного можно сделать вывод о том, что не существует универсального метода, позволяющего провести полный анализ и дать оценку риска инвестиционного проекта. Каждый из рассмотренных выше методов обладает своими достоинствами и недостатками.
Качественные методы позволяют рассмотреть все возможные рисковые ситуации и описать все многообразие рисков рассматриваемого инвестиционного проекта, но получаемые при этом результаты оценки часто обладают не очень высокой объективностью и точностью.
Использование количественных методов дает возможность получить численную оценку рискованности проекта, определить степень влияния факторов риска на его эффективность. К числу недостатков этих методов можно отнести необходимость наличия большого объема исходной информации за длительный период времени (статистический метод); сложности при определении законов распределения исследуемых параметров (факторов) и результирующих показателей (статистический метод, метод Монте-Карло); изолированное рассмотрение изменения одного фактора без учета влияния других (анализ чувствительности, метод проверки устойчивости) и т. д.
Особое внимание хотелось бы уделить недостаткам вероятностного и минимаксного подходов при проведении сценарного анализа, ведь этот метод позволяет наиболее полно описать все возможные условия осуществления инвестиционного проекта. При вероятностном подходе в случае отсутствия информации об объективных вероятностях реализации того или иного сценария приходится применять субъективные оценки, основанные на опыте или суждении, что приводит к проблеме достоверности этих оценок и полученных результатов. К тому же при этом подходе рассматривается только дискретное множество сценариев реализации инвестиционного проекта и оценок их эффективности, а минимаксный подход и вовсе позволяет принимать решения на основании только наилучшего и наихудшего интегральных эффектов.
Преодоление этих недостатков возможно при использовании теории нечетких множеств, позволяющей сформировать полный спектр сценариев реализации инвестиционного проекта. При этом решение принимается не на основе нескольких оценок эффективности проекта, но по всей совокупности этих оценок. Ожидаемая эффективность проекта не является точечным показателем, а представляет собой поле интервальных значений со своим распределением ожиданий, характеризующимся функцией принадлежности соответствующего нечеткого числа. А взвешенная полная совокупность ожиданий позволяет оценить интегральную меру ожидания негативных результатов инвестиционного процесса [18].
Список литературы
1. Андреев, Д. М. Вероятностная модель ставки дисконтирования денежных потоков / Д. М. Андреев // Аудиторские ведомости. – 2002. – № 9. – C. 74–77.
2. Волков, И. Анализ проектных рисков / И. Волков, М. Грачева [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
3. Волков, И. Вероятностные методы анализа рисков / И. Волков, М. Грачева [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
4. Воронцовский, А. В. Инвестиции и финансирование: Методы оценки и обоснования / А. В. Воронцовский. – СПб. : Изд-во С.-Петербургского ун-та, 1998. – 528 с.
5. Дмитриев, М. Н. Количественный анализ риска инвестиционных проектов / М. Н. Дмитриев, С. А. Кошечкин [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
6. Доладов, К. Ю. Экономическая оценка инвестиционного риска при принятии управленческих решений: На примере промышленных предприятий Самарской области : дис. … канд. экон. наук: 08.00.05 / К. Ю. Доладов. – Самара, 2002. – 187 с.
7. Игонина, Л. Л. Инвестиции : учеб. пособие / Л. Л. Игонина; под ред. д-ра экон. наук, проф. В. А. Слепова. – М. : Экономистъ, 2004. – 478 с.
8. Игошин, Н. В. Инвестиции. Организация управления и финансирование : учебник для вузов / Н. В. Игошин. – М. : Финансы, ЮНИТИ, 1999. – 413 с.
9. Ионов, Ю. Г. Риск-предикторы в задачах обоснования управленческих решений : дис. … канд. экон. наук: 08.00.13 / Ю. Г. Ионов. – Воронеж, 2004. – 162 с.
10. Колотынюк, Б. А. Инвестиционные проекты : учебник / Б. А. Колотынюк. – СПб. : Изд-во Михайлова В. А., 2000. – 422 с.
11. Кошечкин, С. А. Концепция риска инвестиционного проекта / С. А. Кошечкин [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
12. Красс, М. С. Математика для экономистов / М. С. Красс, Б. П. Чупрынов. – СПб. : Питер, 2005. – 464 с.
13. Кузьмина, Л. Анализ производственных инвестиций / Л. Кузьмина // Финансовая газета. – 2001. – № 10–13.
14. Липсиц, И. В. Экономический анализ реальных инвестиций : учеб. пособие / И. В. Липсиц, В. В. Коссов. – М. : Экономистъ, 2004. – 347 с.
1. Лукасевич, И. Я. Имитационное моделирование инвестиционных рисков / И. Я. Лукасевич [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
2. Методические рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования / Госстрой России, Министерство экономики РФ, Министерство финансов РФ, Госкомпром России 31 марта 1994 г. № 7-12/47 [Электронный ресурс] // Информационно-правовая система "КонсультантПлюс". – М., 2006.
3. Методические рекомендации по оценке эффективности инвестиционных проектов / Министерство экономики РФ, Министерство финансов РФ, Государственный комитет РФ по строительной, архитектурной и жилищной политике 21.06.1999 N ВК 477 [Электронный ресурс] // Информационно-правовая система "КонсультантПлюс". – М., 2006.
4. Недосекин, А. Новый показатель оценки риска инвестиций / А. Недосекин, К. Воронов [Электронный ресурс]. – Режим доступа: http://www.cfin.ru/finanalysis/invest.
5. Орлова, Е. Р. Инвестиции : курс лекций / Е. Р. Орлова. – М. : Омега-Л, 2003. – 192 с.
6. Станиславчик, Е. Основы инвестиционного анализа / Е. Станиславчик // Финансовая газета. – 2004. – № 11. – C. 7–12.
7. Теплова, Т. В. Финансовые решения: стратегия и тактика : учеб. пособие / Т. В. Теплова. – М. : ИЧП "Издательство Магистр", 1998. – 264 с.
8. Четыркин, Е. М. Финансовый анализ производственных инвестиций / Е. М. Четыркин. – М. : Дело, 1998. – 256 с.
Научный электронный журнал КубГАУ . № 03(19), 2006