Научный электронный журнал КубГАУ . № 01(17), 2006

УДК 681.3:002.53

АНАЛИЗ ЭФФЕКТИВНОСТИ И УСТОЙЧИВОСТИ АПК НА ОСНОВЕ ПОТОКОВЫХ МОДЕЛЕЙ СТОИМОСТИ

Лойко В. И. – д. т. н., профессор

Погосов Ю. Е. – аспирант

Кубанский государственный аграрный университет

Исследование выполнено при финансовой поддержке РГНФ в рамках научно-исследовательского проекта "Экономическая эффективность и устойчивость интегрированных производственных систем агроперерабатывающего комплекса региона", проект № 06-02-38205 а/ю

В статье проведен системный макроэкономический анализ агропромышленного комплекса как системы, все контуры потоков стоимостей которой взаимодействуют через рыночную среду. Анализ проведен с помощью нетрадиционного подхода, использующего аппарат диалектической логики и методологические основы теории цепей.

Большинство видов продукции, производимой сельскохозяйственными предприятиями, прежде чем быть отправленной к потребителю, подлежит переработке. Функцию переработки, а следовательно, и производства в агропромышленном комплексе (АПК) выполняют предприятия перерабатывающей промышленности. Для нормального функционирования основных предприятий АПК необходима производственная инфраструктура, которая обеспечивает выполнение производственных функций предприятий. Это энергетика, водоснабжение, материально-техническое обеспечение, дорожные коммуникации, информационные сети, торговля и т. п.

Важнейшими из производственной инфраструктуры, на наш взгляд, являются производственные предприятия материально-технического снабжения (МТС), являющиеся посредниками между промышленными предприятиями и предприятиями АПК. Без материально-технической подготовки невозможно функционирование производства. Поэтому предприятия МТС занимают одно из приоритетных мест в производственной инфраструктуре и могут быть выделены в отдельный блок.

1. Логистическая система агропромышленного комплекса

Начало 90-х годов в России характеризуется скачкообразным изменением содержания, как внешней среды косвенного воздействия, так и внешней среды внутреннего воздействия, непосредственно влияющего на производство.

Следствием возмущающих воздействий внешней среды является изменение целей, функций и внутренних связей системы.

Таким образом, предпринятая на государственном уровне политическая и экономическая реформы привели к дестабилизации системы АПК, которая проявилась в дестабилизации работы соответствующих предприятий АПК, являющихся элементами этой системы.

Конкретизация приведенных выше положений на уровне логистических системных связей может быть изложена следующим образом. На рисунке 1 приведены укрупненно схемы информационных и материальных потоков, определяющих взаимодействие предприятий АПК и государства до перехода к рынку.

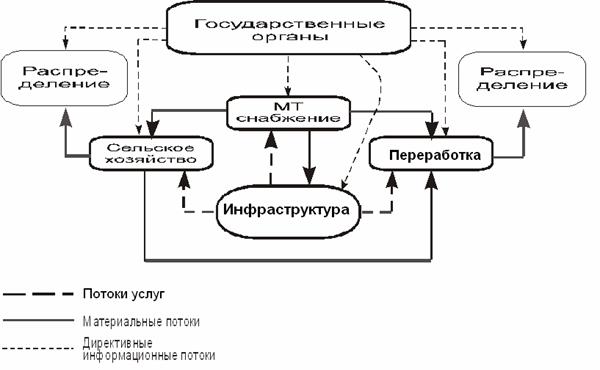
Рисунок 1 – Схема взаимодействия предприятий в директивной
экономике

Недостаток такой системы очевиден. Отсутствуют информационные взаимодействия между элементами системы, что делает ее жесткой, неприспособленной к изменяющейся ситуации (к естественным возмущениям) и ведет к неустойчивости всей системы, а значит, к ее малой эффективности.

Переход к рыночным отношениям предполагает появление рыночной среды (рис. 2), через которую взаимодействуют все предприятия, и идет государственное регулирование экономики. Таким образом, создается совершенно новая система взаимодействия предприятий. В ее рамках функционируют свои рыночные законы взаимодействия (спрос, предложение, конкуренция, конъюнктура рынка и т.д.).

Рыночная среда влечет за собой объективную необходимость изменения производственной структуры, переориентировки направлений материальных, денежных и информационных потоков. Изменение структур и направлений логистических потоков требует оценки с точки зрения эффективности в условиях рынка.

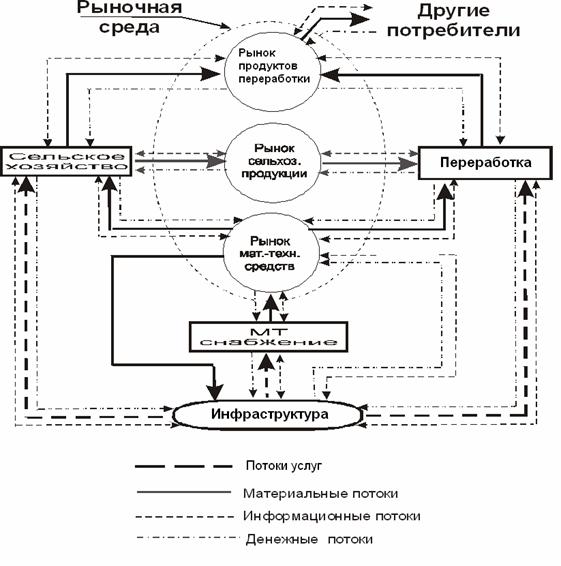
Рисунок 2 – Схема взаимодействия предприятий АПК в условиях рынка

Возникшая рыночная среда фактически является стабилизирующим и регулирующим систему элементом, значительно повышающим ее устойчивость в целом. Объясняется это тем, что приведенные на рисунке 2 рынки являются буферами между входными и выходными потоками предприятий. Наличие буфера в любой системе создает запас устойчивости, что выгодно отличает схему (рис. 2) от схемы на рисунке 1, в которой обрыв любого потока приводит к остановке системы.

В новых условиях возникают проблемы разработки моделей управления АПК.

2. Моделирование экономических систем на основе формализмов диалектической логики

2.1. Структурная схема товарно-денежного обращения

Очевидной истиной представляется, что сущностью и движущей силой любых экономических процессов является стоимость товарно-денежной массы и вложенного в них труда [1]. При этом стоимость многолика и бывает то потребительной, то меновой, то рыночной, то прибавочной и т. д. Однако сущностью всей экономической системы как целого является полезность производимой этой системой продукции, характеризуемая степенью (вероятностью) р удовлетворения потребностей общества. А. А. Денисов [1; 4] предлагает исчислять сущность следующим образом:

где в случае двоичных логарифмов полезность выражается в битах.

2.2. Макроэкономический анализ системы АПК

2.2.1. Логистическая цепь АПК

Структура системы АПК, содержащая рыночную среду как поле взаимодействия логистических (товарно-денежных) потоков, даже в упрощенном виде (рис. 2) сложна для анализа существующими экономико-математическими методами. Задача анализа состоит в том, чтобы определить математически точную взаимосвязь между элементами системы и их характеристиками. Из существующих подходов к анализу экономических систем плодотворным представляется подход А. А. Денисова, использующий для математического описания экономических (логистических) процессов аппарат формализации законов диалектической логики и методологические основы теории цепей. Суть этого подхода состоит в следующем.

Каждая структурная составляющая системы АПК может быть представлена в виде схемы. Учитывая, что в настоящее время в России практически отсутствует рынок автодорожных услуг, уберем из общей цепи АПК контур автодорог. Тогда схема логистических процессов АПК будет иметь следующий вид (рис. 3).

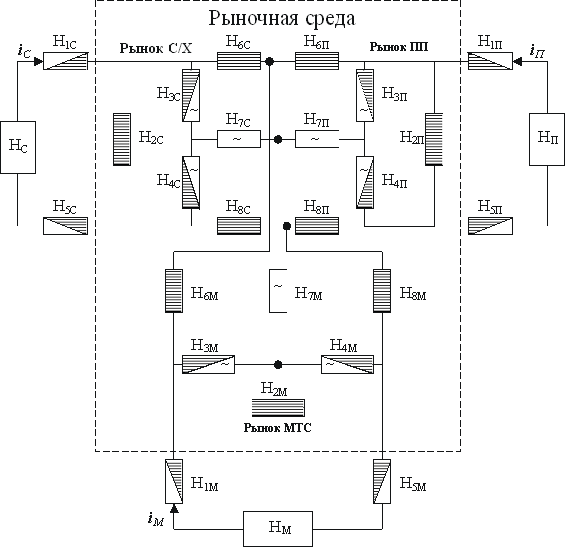
Рисунок 3 – Схема товарно-денежного обращения в системе АПК

На схеме (рис. 3) введены следующие обозначения:

 – экономический потенциал (эффективность) блока системы;

 – процесс производства k-го блока системы (труд – товар);

 – процесс бартерного обмена k-го блока (товар – товар);

 – процесс продажи продукции k-го блока (товар – деньги);

 – процесс покупки товаров k-го блока (деньги – товар);

 – процесс потребления k-го блока (товар – труд);

 – процесс перехода продукции с других рынков на k-й рынок;

 – процесс перехода денег с других рынков на k-й рынок;

 – процесс перехода продукции с k-го рынка на потребление в других блоках АПК;

;

L= c, п, м, где с – сельское хозяйство, п – перерабатывающая промышленность, м – материально-техническое снабжение;

 – оборот стоимостей в k-м блоке АПК.

В полной схеме цепи логистических процессов АПК, изображенной на рисунке 3, ,  и  образуют цепь процессов, протекающих на соответствующем (k-м) рынке. Все вместе они объединяются в цепь рыночной среды АПК. Как видно, получившаяся цепь имеет высокий порядок математической сложности. Учитывая, что каждый процесс имеет две независимые реактивные составляющие, а общее число процессов в изображенной цепи 27, система уравнений, описывающая экономическое равновесие цепи, будет содержать 27 компонентных дифференциальных уравнений второго порядка плюс топологические уравнения для узлов и контуров цепи.

Цепь можно упростить, если учесть следующее.

1.  Рыночная среда, состоящая из цепей рынков отдельных блоков АПК, является внутренним рынком России, поэтому препятствия движению товарно-денежных масс типа таможенных ограничений практически отсутствуют. Следовательно, процессы ,  и  могут быть исключены из схемы.

2. На современном этапе развития рыночных отношений в России удельный вес бартера в процессах обмена мал, в основном обмену сопутствуют два процесса: "товар – деньги" и "деньги – товар". С учетом сказанного процесс  из схемы также можно удалить.

3. Отдельные рынки блоков имеют специализированный характер, поэтому, например, попытки реализации продукции материально-технического снабжения на рынке пищевых продуктов будут обречены на неудачу, и наоборот. Другими словами, специализированные рынки по процессу продаж разделены и, следовательно, перетекание товаров на продажу с одного рынка на другой отсутствует.

4. В отличие от разделенных процессов продаж процессы покупок на отдельных специализированных рынках параллельно объединяются в общий процесс обмена типа "деньги – товар". Причем этот объединенный процесс включает в себя не только денежно-товарные процессы специализированных рынков АПК, но и других рынков, внешних по отношению к рыночной среде системы АПК.

Проведя соответствующие упрощения на схеме рисунка 3, получим цепь логистических процессов АПК в упрощенном виде (рис. 4).

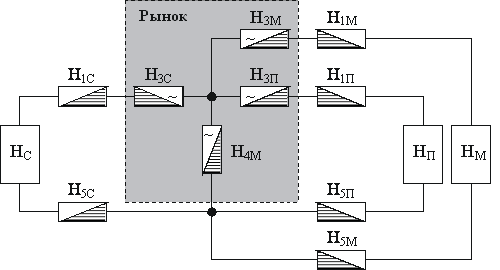
Рисунок 4 – Упрощенная схема товарно-денежного обращения в системе АПК

На схеме (рис. 4) процесс  представляет собой общий процесс покупок, протекающий параллельно на всех специализированных рынках, на которых покупают производители АПК. Любой из изображенных на рисунках 3 и 4 процессов может быть заменен RLC-цепью первого или второго вида. Произведя замены, получим схему (рис. 5).

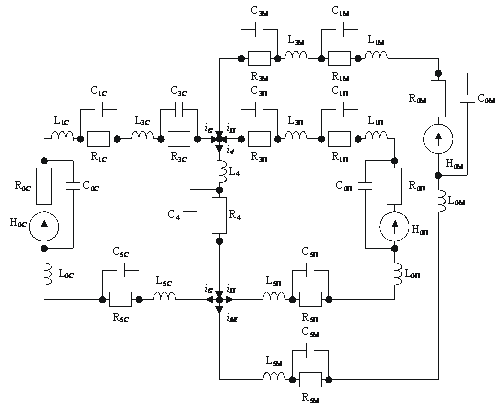
Рисунок 5 – Упрощенная экономическая цепь АПК

Для полного математического описания такой цепи, то есть нахождения зависимостей, позволяющих определить значения оборота стоимостей и падения потенциала в каждой ветви цепи, даже если RLC-цепь каждого процесса будет рассматриваться как одно комплексное сопротивление, потребуется составление 4 независимых топологических уравнений и 10 компонентных. Причем каждое компонентное уравнение – это дифференциальное уравнение второго порядка. Таким образом, дифференциальное уравнение изображенной на рисунке 5 экономической цепи имеет высокий порядок сложности и записывается в общем случае в виде [3]:

,

где – y искомая реакция цепи (оборот стоимостей или падение потенциала в какой-либо ветви);

 – коэффициенты, определяемые параметрами пассивных элементов.

Правая часть этого уравнения – линейная комбинация функций, описывающих внешнее воздействие x(t) на цепь, и их производных. При выключении всех источников экономического потенциала она становится равной нулю.

Дифференциальное уравнение такого порядка сложности является трудно обозримым, и хотя при современных машинных методах его решение не вызывает сомнений, анализ полученного решения является сложной задачей.

Можно предложить следующую (двухэтапную) методику анализа экономической системы, и системы АПК в частности, по ее моделирующей экономической цепи.

1-й этап. Анализ установившегося режима цепи:

а) составление системы алгебраических уравнений экономического равновесия цепи;

б) разрешение системы относительно выбранной ветви;

в) анализ полученного решения.

2-й этап. Анализ переходных процессов цепи:

а) анализ реакции экономической цепи на скачок источника экономического потенциала;

б) анализ реакции экономической цепи на скачок параметра элемента цепи.

При выполнении пунктов а) и б) второго этапа может быть использована одна из методик анализа переходных процессов в линейных инвариантных во времени цепях.

2.2.2. Анализ установившегося режима экономики АПК

В установившемся режиме в экономической цепи действуют постоянные во времени обороты стоимостей и экономические потенциалы. В этом режиме реактивные составляющие процессов не оказывают влияния, и эквивалентная схема цепи может быть представлена на рисунке 6.

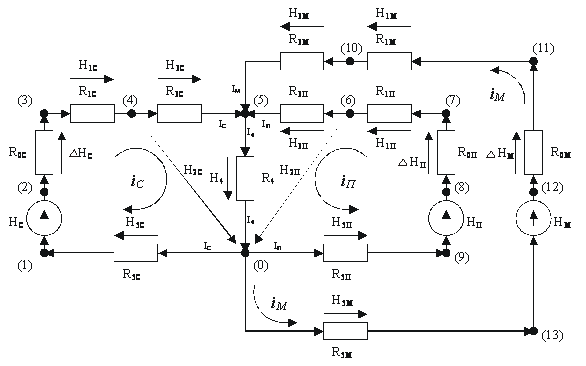
Рисунок 6 – Расширенное топологическое описание цепи оборота стоимостей системы АПК

На схеме (рис. 6) числа в круглых скобках обозначают номера узлов (и ветвей). Топологический граф [3] этой цепи является планарным, и его расширенное представление изображено на рисунке 7а.

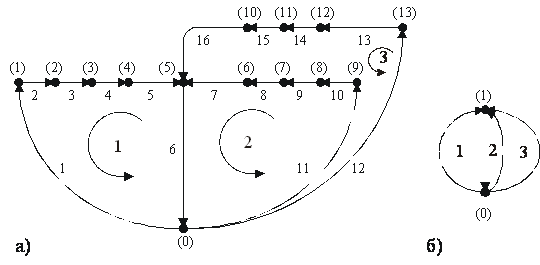
Рисунок 7 – Топологический граф цепи рисунка 6

После преобразования, т. е. уменьшения количества ветвей и узлов, получим сокращенный топологический граф цепи 9 рис. (рис. 7б) (тоже планарный), содержащий два узла, четыре ветви и три окна (ячейки). С помощью графов рисунка 7 составим систему топологических уравнений цепи, содержащую три уравнения равновесия потенциалов и одно – равновесия оборотов стоимостей.

Приведенному на рисунке 7а расширенному графу соответствует матрица  трех основных контуров, в которой номера строк соответствуют номерам основных контуров, а номера столбцов – номерам ветвей [3]:

Вектор стоимостей цепи в соответствии с графом (рис. 7а) имеет вид:

Тогда баланс потенциалов цепи запишем как

Или в виде системы уравнений:

.

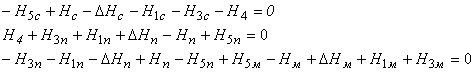После преобразования система независимых уравнений баланса стоимостей цепи примет вид:

Топологическое уравнение равновесия оборотов будет иметь вид:

К полученным четырем топологическим уравнениям (4)–(7) добавятся 13 компонентных уравнений:

Эти 17 независимых уравнений представляют собой систему уравнений равновесия цепи схемы (рис. 6) и позволяют при заданных экономических потенциалах (эффективностях) источников и сопротивлениях процессов определить значения приведенных стоимостей Н всех процессов и их оборотов I.

Общей ветвью моделируемой цепи является ветвь  – общий рынок, на котором покупателями являются производители 3-х подсистем (сельского хозяйства, перерабатывающей промышленности и материально-технического снабжения). Товарооборот , протекающий по этой ветви, определяется уравнением (7), а товарообороты в левой части этого уравнения определяются соотношениями:

В этих соотношениях

Подставив обороты контуров подсистем в (7) и проведя преобразования, получим для рыночного оборота :

где  – проводимость цепи по отношению к зажимам ветви .

При  товарооборот на общем рынке зависит только от суммы оборотов контуров подсистем АПК. В противном случае величина  меньше единицы, и тем меньше, чем больше сопротивление рыночному обороту  по сравнению с R.

2.2.3. Сбалансированность экономики АПК

Выделим из общей цепи рисунка 6 один из контуров, например, контур сельского хозяйства.

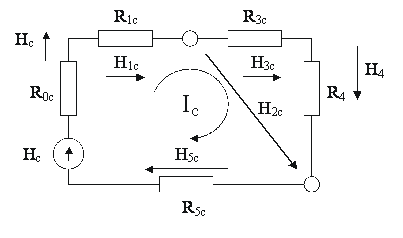
Рисунок 8 – Контур подсистемы сельского хозяйства

Сбалансированность подразумевает равенство производства и потребления (доходов и расходов), из чего следует, что в установившемся режиме для баланса экономики подсистемы (рис. 8) должно быть:

Если выделить в одном из контуров искомый процесс, например прибыль производителя товаров , а сопротивление остальной части контура обозначить Z, тогда схема контура упростится и примет вид, показанный на рисунке 9.

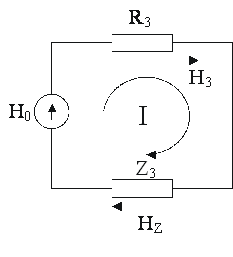
Рисунок 9 – Упрощенная схема контура одной из подсистем

Мощность прибыли производителя  составляет:

где  (рис. 6).

Взяв производную по R и приравняв ее нулю, получим значение , соответствующее максимальной прибыли производителя в единицу времени:

Любое отступление от этого соотношения приводит к уменьшению мгновенной прибыли.

Если выполнить условие (17), то прибыль производителя достигнет значения

и будет равна половине экономического потенциала подсистемы.

Очевидно, подобные соотношения получим и для других процессов. Иными словами, все процессы подсистемы будут стремиться достигнуть максимума потенциала Н, равного .

Требование максимальной прибыли производителя соответствует . Отсюда следует:

,

где .

Аналогично для продавца  и, следовательно,

,                                                         

где .

Солидарная максимальная прибыль достигается при , то есть при

Для контуров ввиду последовательности соединения процессов, то есть всех сопротивлений, производные в выражении (18) равны единицам. Следовательно, условием максимизации солидарной прибыли для всех подсистем является:

При выполнении условия (19) для всех контуров, в них достигаются оптимальные значения оборотов стоимостей, а с учетом условия сбалансированности (16) получим для оптимального оборота каждого контура :

Учитывая, что  является общим для всех контуров, в выражении (20) третье слагаемое в скобках у всех контуров должно быть одинаковым. Поскольку этот же оборот  идет через сопротивление потребления , и падение потенциала на нем тоже равно , получим:

.

Для получения оптимального оборота , максимизирующего солидарную прибыль производителя и продавца при одновременном соблюдении условия сбалансированности, полуразность сопротивления потреблению  и суммы внутреннего сопротивления производству  в каждой подсистеме АПК должна быть равна величине рыночных сопротивлений, то есть

2.2.4. Анализ переходных процессов в экономической цепи АПК

Все экономические процессы, протекающие в моделирующей цепи, могут быть схематично изображены в следующем виде (рис. 10).

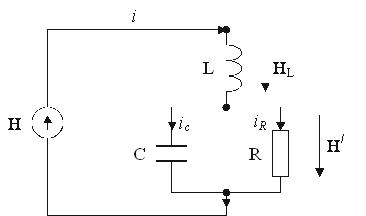
Рисунок 10 – Эквивалентная схема экономического процесса

Используя законы Кирхгофа для цепей, получим для баланса оборотов:

Для баланса стоимостей:

Из (23) получим:

Подставив выражение для  из (24) в (22) и проведя преобразования, получим дифференциальное уравнение экономического процесса в виде:

где i – искомый оборот стоимостей;

R, L, C – параметры процесса.

Правая часть уравнения (25) описывает внешнее воздействие на процесс стоимости Н и ее производной.

Уравнениями, подобными (25), описываются все экономические процессы АПК, кроме блоков эффективности (полезности) каждой из подсистем. Уравнения этих блоков аналогичны, но в правой части содержат .

Применительно к каждой ветви схемы рисунка 5 эти дифференциальные уравнения описывают динамическую взаимосвязь между соответствующим оборотом и его стоимостью. Учитывая закон всеобщей взаимозависимости явлений, отраженный моделирующей цепью, для полного макроописания переходных процессов в макроэкономике АПК необходимо решение системы из 13 дифференциальных уравнений вида (25), связанных топологическими уравнениями. Цепь (рис. 5) характеризуется достаточно высоким порядком сложности, и полный анализ ее устойчивости на переходных режимах экономики возможен лишь машинными методами.

Однако можно сделать некоторые качественные суждения о реакции системы АПК на скачки внешнего воздействия по результатам анализа переходных процессов в отдельном блоке, имеющем лишь второй порядок сложности цепи.

Реакция цепи отдельного экономического процесса
на скачок стоимости

Пусть на цепь экономического процесса (рис. 10) действует источник стоимости, изменяющийся по закону:

При подобном законе изменения h(t) независимые начальные условия цепи имеют нулевые значения, а уравнения цепи запишутся в виде:

.

Для свободной составляющей оборота  все правые части уравнений равны нулю, а характеристическое уравнение цепи

имеет два корня:

,

где  – коэффициент затухания цепи;

 – резонансная частота цепи.

Как известно [3], при малой добротности контура () характеристическое уравнение имеет два различных вещественных отрицательных корня, а выражение для свободной составляющей оборота после коммутации

В этом случае переходной процесс в цепи носит апериодический характер, причем вследствие того, что , экспонента затухает быстрее экспоненты , из-за чего наблюдается некоторый подъем оборота  с последующим спадом до нуля (рис. 11).

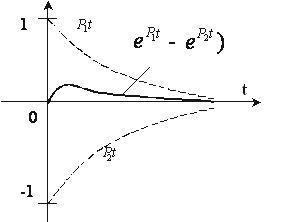
Рисунок 11 – Апериодический переходной процесс

При большой добротности контура () характеристическое уравнение (26) имеет два комплексно-сопряженных корня:

,

где  – частота свободных колебаний в цепи.

Тогда уравнение (27) может быть преобразовано к виду:

где  = .

При  наступает критический (неустойчивый) режим цепи, определяющий границу между апериодическим и колебательным режимами.

Учитывая выражения для  и  через параметры элементов цепи, получим условия:

Другими словами, экономический процесс в переходном режиме имеет апериодический характер, если удвоенное сопротивление обороту стоимости будет меньше корня квадратного из отношения регидности к емкости процесса.

Для получения временной характеристики полного оборота стоимости воспользуемся операторным методом анализа [3]. Операторная эквивалентная схема экономического процесса приведена на рисунке 12.

Рисунок 12 – Операторная эквивалентная схема экономического процесса

Для изображения оборота стоимости I(p) получим:

,

где  и  – корни характеристического уравнения, полученные ранее (26).

Преобразуем это выражение к виду, удобному для перехода к оригиналу:

.

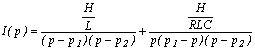Оригиналом полученного изображения будет полный оборот в цепи экономического процесса:

Это выражение позволяет определить оборот стоимости в цепи экономического процесса в любой момент времени в диапазоне от t=0 до .

Первое слагаемое в правой части уравнения (30) – это уже исследованная свободная составляющая переходного процесса, второе слагаемое – принужденная составляющая, усложняющая вид переходного процесса. Но поскольку корни характеристического уравнения (26) определяют и ход процесса во втором слагаемом, условие отсутствия колебаний остается прежним (28).

В проведенном анализе цепи величина H – это величина скачка, вызванная скачком эффективности (полезности) подсистемы  и определяемая коэффициентом передачи для соответствующей ветви. Но в процессе функционирования системы установившийся режим может быть нарушен из-за скачкообразного изменения одного или нескольких сопротивлений обороту. В этом случае переходной процесс в цепи отдельного экономического блока будет протекать аналогично рассмотренному, а величина скачка H может быть определена из анализа установившихся процессов до и после скачка.

Наиболее чувствительным к изменению экономической, финансовой и политической среды в цепи АПК является сопротивление обороту на общем рынке . Поэтому предположим, что произошло скачкообразное изменение на величину . Так как сопротивление  является общим для всех контуров (рис. 6), то в каждом из них произойдет скачок товарооборота в большую или меньшую сторону в зависимости от знака скачка .

,                                           

где  – эффективность соответствующего контура;

 – суммарное сопротивление оборота соответствующего контура до скачка.

Скачок же стоимости на составит:

где  – рыночное сопротивление обороту до скачка.

Из выражения (31) с очевидностью следует, что завышение цен на общем рынке после окончания переходного процесса вовсе не соответствует ожидаемой прибыли у продавцов, так как  находится как в числителе, так и в знаменателе.

Чтобы определить , при котором скачок стоимости  достигает максимума, приравниваем производную (31) по  нулю. Получим , т. е. для максимального скачка  прибыли продавцов, необходимо увеличение  в два раза.

Однако если продавцы решили увеличить в два раза сопротивление обороту (), надеясь на двойную прибыль, то в связи с уменьшением товарооборота прирост прибыли составит только

.                                                

Эта формула действительна только для скачка , и показывает, что реальное увеличение прибыли существенно ниже ожидаемого. Например, при , что соответствует более менее солидарному распределению прибыли при балансе экономики, получим прирост прибыли:

,

а рыночный оборот при этом уменьшится на величину , где  – оборот в контуре до скачка .

Увеличение же мощности прибыли продавцов произойдет на величину:

,

где  – мощность прибыли продавцов до скачка;

 – мощность прибыли продавцов после скачка.

Проведенный макроэкономический анализ системы показал, что при использовании формализмов диалектической логики устанавливаются строгие соотношения между параметрами экономических процессов, и управление ими может осуществляться как изменением эффективностей соответствующих подсистем, так и изменением параметров процессов R, C, L.

Но в настоящее время не существует методов для определения эффективностей и параметров процессов R, C, L. Это обусловлено тем, что нет обоснованных методик и подходов для определения этих коэффициентов. В дальнейшем планируется разработка методов по нахождению параметров R, C, L, что позволит применить выведенные соотношения для макроэкономического анализа АПК.

Выводы

1. Предложена методика макроэкономического моделирования эффективности и устойчивости системы АПК, использующая потоковые модели стоимости.

2. Модифицирована эквивалентная экономическая цепь системы АПК, и получены уравнения и условия ее баланса в установившемся режиме.

3. Исследованы переходные режимы отдельного экономического процесса и показаны условия его устойчивости.

4. Проведен анализ цепи системы АПК для скачка сопротивления обороту стоимостей на общем рынке и получены соотношения, позволяющие прогнозировать уровни скачков цен и мощностей товарооборота.

Список литературы

1.     Денисов, А. А. Макроэкономическое управление и моделирование: Пособие для начинающих реформаторо / А. А. Денисов. – СПб : Омега, 1997.

2.     Лойко, В. И. Методическое обеспечение структурной перестройки предприятий агропромышленного комплекса в переходный период / В. И. Лойко. – Краснодар : Изд-во КубГАУ, 2000.

3.     Попов, В. П. Основы теории цепей : учебник для вузов / В. П. Попов. – М. : Высш. шк., 1985.

4.     Денисов, А. А. Теория систем и системный анализ / А. А. Денисов, В. Н. Волкова. – М. : Политехника, 1999.

Научный электронный журнал КубГАУ . № 01(17), 2006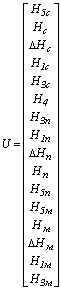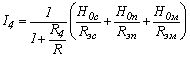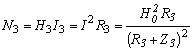