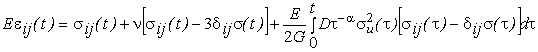Научный электронный журнал КубГАУ . № 08(16), 2005
УДК 622.011.43
КВАЗИСТАТИЧЕСКИЙ АНАЛИЗ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ВЯЗКОУПРУГОГО ПОЛУПРОСТРАНСТВА С ОСЕСИММЕТРИЧНОЙ ПОЛОСТЬЮ
Аршинов Г. А. – к. ф.-м. н.
Кубанский государственный аграрный университет
Исследуется релаксация напряжений вблизи осесимметричных полостей различной конфигурации. Учитывается нелинейная ползучесть вмещающего массива каменной соли.
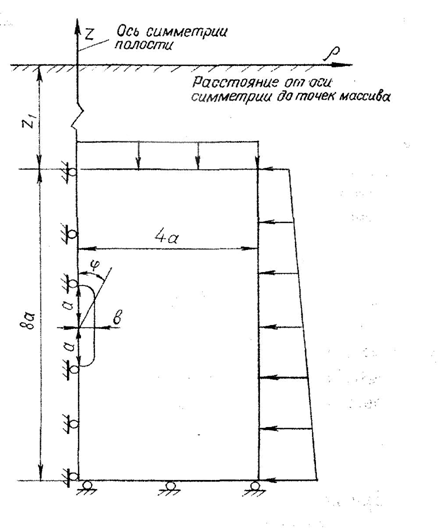
Расчетная модель строилась из предположения, что осесимметричная полость глубокого заложения образована в однородном изотропном весомом массиве, невозмущенное напряженное состояние которого определяется гидростатическим, линейно зависящим от глубины сжимающим полем напряжений и не испытывает влияния полости при удалении от последней на четыре ее характерных размера.
На горизонтальной границе внешнего
контура области, определенной четырьмя характерными размерами полости,
действует равномерно распределенная нагрузка ![]() , соответствующая давлению массива на глубине
, соответствующая давлению массива на глубине ![]() , а на
вертикальной – распределенная нагрузка
, а на
вертикальной – распределенная нагрузка ![]() . Нижняя горизонтальная граница не
перемещается в вертикальном направлении (рис. 1). Выделенная область массива
аппроксимируется сеткой треугольных конечных элементов, представляющих собой
сечение меридиональной плоскостью кольцевых треугольных элементов, с помощью
которых моделируется массив с полостью.
. Нижняя горизонтальная граница не
перемещается в вертикальном направлении (рис. 1). Выделенная область массива
аппроксимируется сеткой треугольных конечных элементов, представляющих собой
сечение меридиональной плоскостью кольцевых треугольных элементов, с помощью
которых моделируется массив с полостью.
Уравнения, связывающие напряжения и деформации, были приняты в виде
|
(1) |
с параметрами ![]() ;
; ![]() =0,3;
=0,3; ![]() =0,73;
=0,73; ![]() (объемный вес галита
(объемный вес галита ![]() [1].
[1].
|
||||
Рисунок 1 – Схема к расчету осесимметричной полости, заключенной в массиве каменной соли |
Промежуток времени [0, t] делится на некоторое число интервалов ![]() таким образом, чтобы с заданной степенью точности приращение
деформации ползучести в каждом из них определялось напряжениями, достигнутыми к
моменту времени
таким образом, чтобы с заданной степенью точности приращение
деформации ползучести в каждом из них определялось напряжениями, достигнутыми к
моменту времени ![]() (k=1,2,…,L), т.е. в каждом промежутке
(k=1,2,…,L), т.е. в каждом промежутке ![]() можно положить
можно положить
|
(2) |
Согласно (1) приращения деформации ползучести за k-й интервал
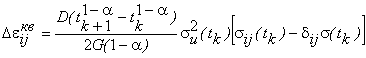 .
.
Вышеприведенные выражения принимаются
за начальные деформации ![]() и
решается система линейных алгебраических уравнений относительно приращений
узловых перемещений
и
решается система линейных алгебраических уравнений относительно приращений
узловых перемещений ![]() ,
где К – матрица жесткости системы конечных элементов, а
,
где К – матрица жесткости системы конечных элементов, а ![]() – вектор начальной узловой
нагрузки.
– вектор начальной узловой
нагрузки.
По найденным из ![]() вычисляется полное приращение
деформаций
вычисляется полное приращение
деформаций ![]() в е-м
конечном элементе, а затем и приращение упругой составляющей
в е-м
конечном элементе, а затем и приращение упругой составляющей ![]() . В соответствии с
законом Гука в каждом элементе определяется приращение напряжений
. В соответствии с
законом Гука в каждом элементе определяется приращение напряжений ![]() , вызванное приращением деформаций
ползучести
, вызванное приращением деформаций
ползучести ![]() за
время
за
время ![]() . Сумма
. Сумма ![]() и
и ![]() дает новое поле напряжений, по которому
вычисляется приращение вязких деформаций в очередном временном интервале
дает новое поле напряжений, по которому
вычисляется приращение вязких деформаций в очередном временном интервале ![]() . Шаговая процедура по времени заканчивается, как только поле
напряжений стабилизируется.
. Шаговая процедура по времени заканчивается, как только поле
напряжений стабилизируется.
Изложенный алгоритм реализован в комплексе программ, с помощью которых рассчитывалось напряженное и деформированное состояние мгновенно образованных равнообъемных, свободных от нагрузки осесимметричных полостей различных форм: шаровой, эллипсоидальной, цилиндрической с шаровыми торцами и цилиндрической с шаровой потолочиной и плоским основанием.
Центры рассматриваемых хранилищ располагались на глубине Н=1000 м, а отношение характерных размеров в/а для эллипсоидальных конфигураций составляло 0,4, для цилиндрических - 0,2 и 0,4 соответственно. Конечно-элементная аппроксимация состояла из 240 кольцевых конечных элементов треугольного поперечного сечения и 147 узловых окружностей.
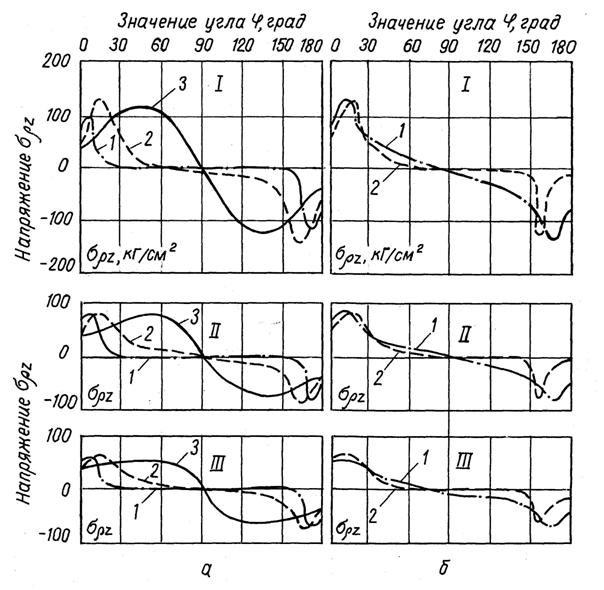
Рассмотрим полученные результаты. На
рисунках 2-5 приведены
расчетные эпюры напряжений вблизи поверхности (0,8-1,5 м от нее), емкостей в зависимости
от времени t и угла ![]() (рис. 1).
(рис. 1).
|
Рисунок 2 – Релаксация компоненты а) 1 - цилиндрической с шаровыми торцами (в/а = 0,2); 2 - той же геометрии (в/а = 0,5); 3 - шаровой; б) 1 - эллипсоидальной (в/а = 0,4); 2 - цилиндрической с шаровой потолочиной и плоским основанием (в/a = 0,4) |
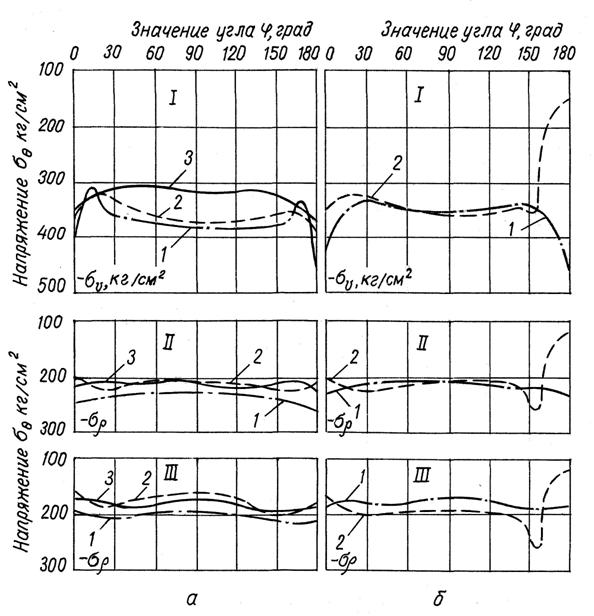
Из рисунков 2-5 следует, что геометрия
полостей-газохранилищ в наибольшей степени влияет на упругое распределение
напряжений, которое можно рассматривать как начальное для момента времени t=0. Все эпюры напряжений,
соответствующие этому моменту, существенно отличаются друг от друга, особенно в
областях интенсивного изменения напряжений. При t>0 разворачивается процесс нелинейной ползучести в
окрестности полости, вызывающей релаксацию напряжений. Последняя интенсивна в
первые часы после образования полости. Значительные изменения поля напряжений
приурочены к местам их максимальной концентрации (![]() ), сглаживаемой за счет релаксации.
), сглаживаемой за счет релаксации.
|
Рисунок 3 –
Релаксация компоненты а) 1 -цилиндрической с шаровыми торцами (в/а = 0,2); 2 - той же геометрии (в/а = 0,4); 3 - шаровой; б) 1 - эллипсоидальной (в/а = 0,4); 2 - цилиндрической c шаровой потолочиной и плоским основанием (в/а = 0,4) |
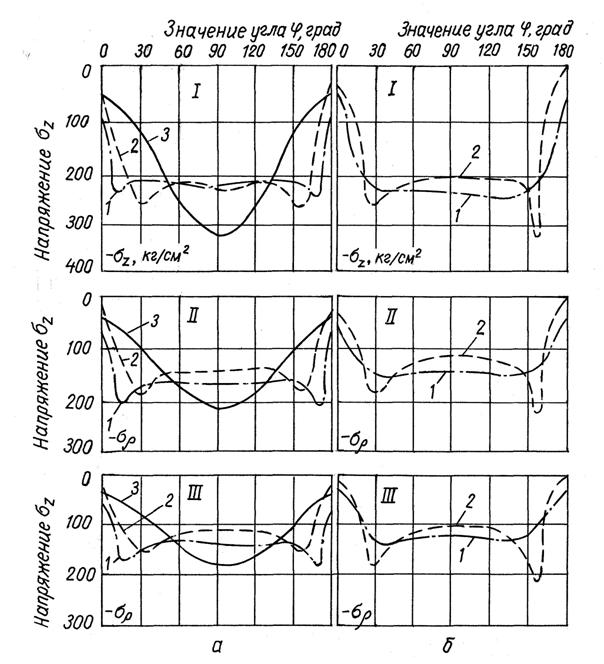
Так, к 30 ч компонента ![]() в
точках пересечения оси 0z с
эллипсоидальной и комбинированной цилиндрической полостями уменьшается в 2
раза, с шаровой – в 1,7 раза. На участках менее интенсивной концентрации
напряжений релаксация выражена слабее.
в
точках пересечения оси 0z с
эллипсоидальной и комбинированной цилиндрической полостями уменьшается в 2
раза, с шаровой – в 1,7 раза. На участках менее интенсивной концентрации
напряжений релаксация выражена слабее.
|
Рисунок 4 –
Релаксация компоненты а) 1- цилиндрической с шаровыми торцами (в/а = 0,2); 2 - той же геометрии (в/а = 0,4); 3 - шаровой; б) 1 - эллипсоидальной (в/а = 0,4); 2 - цилиндрической с шаровой потолочиной и плоским основанием (в/а = 0,4) |
Аналогичная картина наблюдается и для
компонент ![]() ,
, ![]() ,
, ![]() ,
так как процессы ползучести и релаксации органично взаимосвязаны.
,
так как процессы ползучести и релаксации органично взаимосвязаны.
|
Рисунок 5 –
Релаксация компоненты а) 1 - цилиндрической с шаровыми торцами (в/а = 0,2); 2 - той же геометрии(в/а = 0,4); 3 - шаровой; б) 1 - эллипсоидальной (в/а = 0,4); 2 - цилиндрической с шаровой потолочиной и плоским основанием (в/а = 0,4) |
Ползучесть, описываемая соотношениями (1), и вызываемая ею релаксация напряжений носят затухающий характер. В первые 30 ч после образования полости деформации наиболее интенсивны, и в этом временном интервале происходят значительные изменения поля напряжений вблизи полостей.
По истечении 30 ч ползучесть среды
ослабевает, вызывая незначительное перераспределение напряжений. Достаточно
отметить, что в промежутке времени от 30 ч до года значение напряжений ![]() в
вершинах эллипсоидальной полости уменьшилось приблизительно в 1,2 раза, тогда
как в течение первых 30 ч - в 2 раза. Подобным образом ведут себя и остальные компоненты тензора
напряжений. После годичного промежутка времени ползучесть массива практически
прекращается и напряженное состояние стабилизируется.
в
вершинах эллипсоидальной полости уменьшилось приблизительно в 1,2 раза, тогда
как в течение первых 30 ч - в 2 раза. Подобным образом ведут себя и остальные компоненты тензора
напряжений. После годичного промежутка времени ползучесть массива практически
прекращается и напряженное состояние стабилизируется.
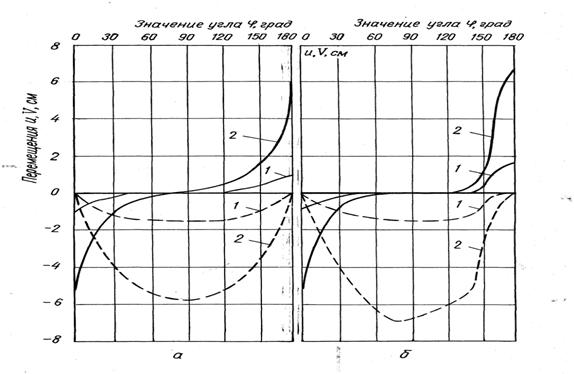
Далее обратимся к анализу
распределения перемещений, вызванных деформированием массива каменной соли. На
рисунках 6-8 приведены
расчетные эпюры дополнительных перемещений точек поверхности полости,
фиксируемых углом ![]() (рис.
1), которые соответствуют начальному (t=0) и конечному (t=1 год) моментам времени.
(рис.
1), которые соответствуют начальному (t=0) и конечному (t=1 год) моментам времени.
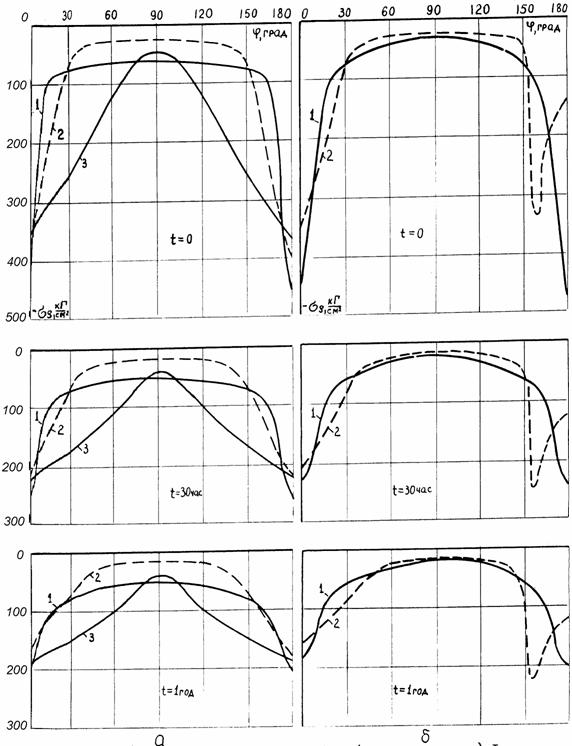
Перемещения, вызванные ползучестью
среды, значительно превосходят соответствующие им упругие перемещения. Так,
например, по истечении года максимальные перемещения (![]() ) превышают упругие (t=0) приблизительно в 5 раз в случае
шаровой конфигурации; в 4-7
раз – цилиндрической с шаровыми торцами (в/а = 0,2 и в/а = 0,4) и
эллипсоидальной (в/а = 0,4); в 4-6 раз – цилиндрической с шаровой потолочиной и плоским
основанием конфигураций полостей.
) превышают упругие (t=0) приблизительно в 5 раз в случае
шаровой конфигурации; в 4-7
раз – цилиндрической с шаровыми торцами (в/а = 0,2 и в/а = 0,4) и
эллипсоидальной (в/а = 0,4); в 4-6 раз – цилиндрической с шаровой потолочиной и плоским
основанием конфигураций полостей.
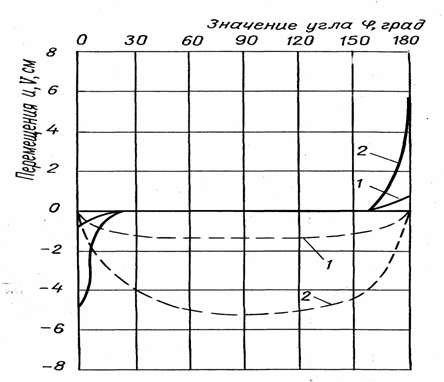
Аналогично распределению напряжений наибольшие градиенты перемещений наблюдаются в области потолочины и оснований хранилищ, причем более интенсивно меняется вертикальная составляющая вектора перемещений V.
Максимальные смещения приурочены к
вершинам (![]() ) и
экваториальной окружности (
) и
экваториальной окружности (![]() ). Сравнение максимальных вертикальных
). Сравнение максимальных вертикальных ![]() ) и горизонтальных u (
) и горизонтальных u (![]() ) начальных (t=0) перемещений показало, что первые значительно
меньше вторых для всех полостей, исключая шаровую и цилиндрическую с шаровой
потолочиной и плоским основанием. В процессе ползучести это различие стирается:
максимальные значения компонент U, V приблизительно становятся равными. Таким образом, ползучесть массива каменной
соли сглаживает влияние особенностей геометрии хранилища на перемещение точек
его поверхности, что вполне согласуется с характером изменения эпюр напряжений
в процессе релаксации. Сопоставление упругих деформаций с вязкими и
максимальных значений перемещений точек поверхности полости с ее исходными
размерами показало, что для данного типа вязкоупругой среды характерны малые
деформации, практически не изменяющие начальные размеры, а следовательно, и
объемы хранилищ.
) начальных (t=0) перемещений показало, что первые значительно
меньше вторых для всех полостей, исключая шаровую и цилиндрическую с шаровой
потолочиной и плоским основанием. В процессе ползучести это различие стирается:
максимальные значения компонент U, V приблизительно становятся равными. Таким образом, ползучесть массива каменной
соли сглаживает влияние особенностей геометрии хранилища на перемещение точек
его поверхности, что вполне согласуется с характером изменения эпюр напряжений
в процессе релаксации. Сопоставление упругих деформаций с вязкими и
максимальных значений перемещений точек поверхности полости с ее исходными
размерами показало, что для данного типа вязкоупругой среды характерны малые
деформации, практически не изменяющие начальные размеры, а следовательно, и
объемы хранилищ.
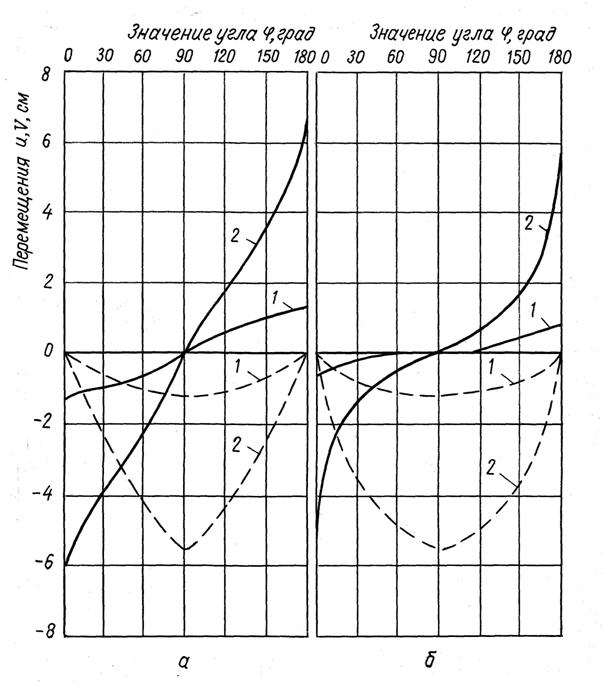 |
| Рисунок 6 – Компоненты перемещений точек
поверхности полости: а) - шаровой; б) – эллипсоидальной (в/а = 0,4) |
|
Рисунок 7 – Компоненты перемещений точек поверхности полости: а) - цилиндрической с шаровыми торцами (в/а = 0,4); б) - цилиндрической с шаровой потолочиной и плоским основанием (в/а = 0,4) |
|
Рисунок 8 – Компоненты перемещений точек цилиндрической поверхности с шаровыми торцами полости (в/а = 0,2) |
Таким образом, в квазистатических задачах нелинейная вязкоупругость существенным образом влияет на процесс деформирования среды в окрестности осесимметричной полости, вызывая заметное перераспределение концентрации напряжений и увеличение перемещений точек сред в сравнении с упругими перемещениями.
Список литературы
1. Ержанов, Ж. С. Ползучесть соляных пород / Ж. С. Ержанов, Э. И. Бергман. – Алма-Ата : Наука, 1977.
Научный электронный журнал КубГАУ . № 08(16), 2005