Научный электронный журнал КубГАУ . № 08(16), 2005

УДК 622.011.43

ИССЛЕДОВАНИЕ ПРОЦЕССА ДЕФОРМИРОВАНИЯ МАССИВА КАМЕННОЙ СОЛИ, СОДЕРЖАЩЕГО ПОДЗЕМНОЕ НЕФТЕГАЗОХРАНИЛИЩЕ

Аршинов Г. А. – к. ф.-м. н.

Кубанский государственный аграрный университет

Рассматриваются условия сходимости метода упругих решений в задачах нелинейной теории ползучести при исследовании распределения напряжений вблизи осесимметричных полостей различной конфигурации, образованных в отложениях каменной соли.

Практически важные задачи, связанные с добычей солей, а также размещением в их толщах различного рода подземных хранилищ, не могут быть решены без глубокого изучения физико-механических свойств соляных пород. Последние относятся к классу материалов, в деформировании которых доминирующую роль играют нелинейные процессы ползучести и релаксации. Это неоднократно подтверждалось многочисленными экспериментальными исследованиями образцов различных месторождений и натурными наблюдениями. Для большей части опубликованных работ характерно стремление изучить упругие, прочностные, реологические свойства, а также построить уравнения механического состояния соляных пород на основе одноосных испытаний, что не гарантирует возможности распространения полученных результатов на сложное напряженное состояние. Реже встречаются многоосные опыты, подавляющая часть которых выполнена в камере Кармана.

Приведем результаты испытания прочностных и деформативных свойств образцов солей Солигорского месторождения при одноосном сжатии [1]. Ползучесть призматических образцов размером  см исследовалась на гидравлических и пружинных прессах при циклически возрастающей и длительно действующей нагрузках. Установлено, что мгновенное (t=0) деформирование соляных образцов линейно, а при t>0 развивается процесс нелинейной ползучести каменной соли с преобладанием необратимых деформаций.

Подобные процессы могут быть описаны уравнением состояния вида:

причем уровень нелинейности деформирования зависит от степени нагруженности образца: для нагрузок, не превышающих 0,4 ( - напряжение разрушения при одноосном сжатии), получены практические линейные изохронны, т.е. в этом случае можно воспользоваться уравнениями линейной теории вязкоупругости [2], успешно применяемыми для описания ползучести горных пород. Если нагрузки не удовлетворяют упомянутому ограничению, то нелинейный член в уравнении (1) необходимо сохранить. Более того, при значительных нагрузках в уравнении (1) можно опустить второе слагаемое без ущерба точности кривых ползучести.

Лабораторные испытания трубчатых образцов различных соляных пород в условиях плоской деформации [3] позволили обобщить уравнение (1) на случай сложного напряженного состояния и для больших нагрузок представить уравнение механического состояния солей в виде уравнения, представляющего собой уравнения нелинейной вязкоупругости

ядро которых

или уравнения теории старения, если

где  – интенсивность напряжений,  D – параметры ползучести.

Использование теории старения наиболее предпочтительно. В этом случае второй член в уравнениях (2) дает необратимую деформацию ползучести, что вполне согласуется с экспериментами [3]. В результате обработки лабораторных данных и натурных наблюдений за конвергенцией горизонтальных протяженных выработок круглого поперечного сечения определены параметры ползучести ядер (3), (4).

Согласно данным [3], соотношения линейной вязкоупругости (когда Р(t)=0) применимы при расчете мало заглубленных подземных сооружений, возводимых в соляных толщах. В этом случае задача упрощается в силу независимости поля напряжений от времени.

Нелинейность уравнений (2), которую необходимо учитывать при исследовании подземных сооружений глубокого заложения, значительно усложняет анализ напряженного и деформированного состояния, поскольку неизвестен вид функциональной зависимости напряжений от времени.

Задачи теории ползучести с физической нелинейностью не столь наглядны, как линейные, но и они в ряде случаев успешно решаются методом конечных элементов, что убедительно показано в монографии [4]. Метод конечных элементов распространяется на решение нелинейных задач с помощью метода упругих решений, описанного в монографиях. К наиболее распространенным итерационным схемам относятся так называемые методы переменных упругих параметров, начальных напряжений и деформаций, применение каждого из которых продиктовано соображениями удобства и мощностью ЭВМ.

Линеаризация физически нелинейных задач в методе переменных упругих параметров основывается на предположении о зависимости матрицы упругих постоянных от уровня достигнутой деформации:

где [D] - матрица упругих констант.

В задачах теории ползучести исследуемый промежуток времени дробится на малые интервалы, в каждом из которых матрица упругости корректируется по результатам расчета в предыдущем временном шаге на основе уравнения (5). Итерационный процесс продолжается, пока расчетные напряжения в двух соседних временных интервалах будут близки с заданной степенью точности. Метод переменных упругих параметров не экономичен с точки зрения затрат машинного времени: в каждом временном шаге заново строится матрица жесткости системы конечных элементов.

Метод начальных напряжений удобен, если уравнения механического состояния разрешимы относительно напряжений

В этом случае путем подбора начальных напряжений, сводимых к вектору начальных узловых сил, искомые значения напряжений определяются последовательным решением ряда задач линейной теории упругости. Итерационный процесс осуществляется следующим образом. Расчетный временной интервал вновь разбивается на необходимое число точек. При t=0 решается краевая задача линейной теории упругости. По распределению упругих деформаций  и согласно выражению (6) строятся начальное поле напряжений и соответствующий ему суммарный вектор начальной узловой нагрузки , затем устанавливаются поправки в результат первого упругого расчета. Для следующего временного шага процедура повторяется вновь, но с откорректированным полем напряжений. Итерационный процесс прекращается, как только в двух смежных временных шагах напряжения станут достаточно близкими.

Метод начальных деформаций, во многом аналогичный процедуре начальных напряжений, применяется в случае разрешимости уравнений механического состояния относительно деформаций: . В этом случае корректировка упругих решений осуществляется подбором начальных деформаций .

Обратимся к вопросу сходимости метода упругих решений в задачах нелинейной теории ползучести. Математическое обоснование уравнений механического состояния нелинейной теории вязкоупругости предложено в работе [5]. Вводя гильбертовы пространства ,  функций Е(), , под которыми понимаются соответственно тензора деформаций  и напряжений , определенные на отрезке времени [0, t], и задавая нормы  и  в виде

,

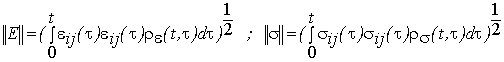где ,  - положительные функции памяти, авторы показывают, что любые аналитические в окрестности нуля операторы F, Q, отображающие соответственно  на и  на  =F(E), E=Q(), можно представить в виде рядов:

где

,.

Точность аппроксимации операторов F, Q зависит от числа членов, сохраняемых в рядах (7) при замене бесконечных сумм конечными. Авторами получены условия, при которых операторы F и Q взаимно обратны, причем обращение осуществляется методом сжатых отображений.

Рассмотрим уравнения механического состояния, связывающие компоненты девиаторов тензоров напряжений и деформаций и вытекающие из (2), (4), в виде

и введем оператор Р

где 0£, ,  - интенсивность деформаций, а ядро

.

Предположим, что ,  - элементы пространства С[0,] с нормой . Известно [6], что операторы типа (9), определенные на С[0,], дифференцируемы в этом пространстве по Фреше. В частности, производная по Фреше от Р определяется соотношением:

,

где

,

при этом суммирование по i не производится.

Выделим в С[0,] шар . Если в R имеет место неравенство , то для любых  

В силу условия (10) при L<1 оператор Р является сжимающим в R, т.е. его неподвижную точку можно найти методом последовательных приближений, принимая за начальное нулевое приближение, удовлетворяющее неравенству [5]

Определим условия, при которых L<1:

.

Таким образом, , если

Для того чтобы удовлетворить (11), примем

предполагая, что условия (12), (13) выполнены, и используя (9), в результате второго приближения получим уравнение:

где  - интенсивность напряжений.

Это уравнение в рамках упомянутого приближения обратно (8) и с той же точностью аппроксимирует реальный оператор, связывающий девиаторы деформаций и напряжений.

В работе [7] исследована сходимость метода упругих решений для уравнений механического состояния вида

где ядра разбиваются на сингулярную и регулярную составляющие:

.

При этом некоторая вектор-функция u называется обобщенным решением краевой задачи для области V с границей S:

если u удовлетворяет интегральному тождеству:

,

где .

Далее вводится скалярное произведение для некоторых дифференцируемых функций

и ищется обобщенное решение в пространстве Н, которое получается замыканием по норме (18) множества дважды непрерывно дифференцируемых векторов-функций, удовлетворяющих (16). При этом метод упругих решений краевой задачи (16), (19) для уравнений механического состояния (15) сходится к единственному решению, если уравнение  однозначно разрешимо в виде , а функция  таковы, что для любого :

,

причем , а начальное приближение выбрано из условия , где М - константа, ограничивающая .

Уравнения (8) вытекают из (15), если в последних положить  и во втором интеграле вместо  ввести функцию .

Приведенная теорема о сходимости метода упругих решений распространяется на (8), а следовательно, и на уравнения (14). Если , то для удовлетворения неравенства (19) достаточно положить . Тогда метод упругих решений для уравнений механического состояния (8), (14) сходится, если  и начальное приближение  удовлетворяют неравенствам:

В промежутке времени [ ч] компоненты девиаторов напряжений и деформаций, соответствующие параметрам упругости и ползучести каменной соли, обеспечивают выполнение условий (12), (13) и (20). За начальное приближение  принимается упругое решение.

Список литературы

1. Ержанов, Ж. С. Об оценке устойчивости формы осесимметричной полости в соляном массиве / Ж. С. Ержанов, Г. А. Аршинов, Э. И. Бергман // Известия АН КазССР. Сер. Физ.-мат. – 1974. – № 5.

2. Ержанов, Ж. С. Теория ползучести горных пород и ее приложения / Ж. С. Ержанов. – Алма-Ата : Наука, 1964.

3. Ержанов, Ж. С. Ползучесть соляных пород / Ж. С. Ержанов, Э. И. Бергман. – Алма-Ата : Наука, 1977.

4. Зенкевич, О. С. Метод конечных элементов в технике / О. С. Зенкевич. – М. : Мир, 1975.

5. Илюшин, А. А. Основы математической теории термовязкоупругости / А. А. Илюшин, Б. Е. Победря. – М. : Наука, 1970.

6. Люстерник, Л. А. Элементы функционального анализа / Л. А. Люстерник, В. И. Соболев. – М. : Наука, 1965.

7. Победря, Б. Е. О сходимости метода упругих решений в нелинейной вязкоупругости / Б. Е. Победря // ДАН АН СССР. – 1970. – Т. 195. – № 2.

Научный электронный журнал КубГАУ . № 08(16), 2005