Научный электронный журнал КубГАУ . № 08(16), 2005
УДК 622.011.43
КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ УПРУГОГО МАССИВА, СОДЕРЖАЩЕГО ОСЕСИММЕТРИЧНУЮ ПОЛОСТЬ
Аршинов Г. А. – к. ф.-м. н.
Кубанский государственный аграрный университет
Рассматривается конечно-элементная модель расчета напряженно-деформированного состояния упругого полупространства, содержащего осесимметричную полость.
Модель строится из следующих соображений. Допустим, что в упругом
однородном изотропном полупространстве образована осесимметричная (с вертикальной
осью симметрии) полость с центром на глубине Н и максимальным
характерным размером а. Предполагая, что а/Н<<1, и учитывая
малость влияния полости на напряженное состояние окружающего ее массива вне
шара (центры полости и шара совпадают) радиуса 4а, заменим весомое
полупространство, содержащее емкость, невесомым круглым цилиндром с полостью,
по верхнему торцу и боковой поверхности которого равномерно распределены
сжимающие усилия ![]() (
(![]() – объемный вес массива) и
– объемный вес массива) и ![]() , а нижний торец
опирается на жесткое основание. Выделенную область массива с полостью
аппроксимируем совокупностью кольцевых конечных элементов треугольного
поперечного сечения и в силу осесимметричности рассмотрим лишь половину
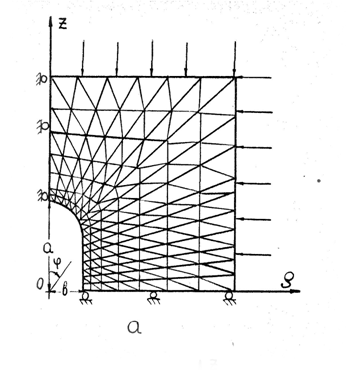
меридионального сечения полученной аппроксимации (рис. 1в). При наличии у
полости экваториальной плоскости симметрии достаточно рассмотреть четверть
указанного сечения (рис. 1а).
, а нижний торец
опирается на жесткое основание. Выделенную область массива с полостью
аппроксимируем совокупностью кольцевых конечных элементов треугольного
поперечного сечения и в силу осесимметричности рассмотрим лишь половину
меридионального сечения полученной аппроксимации (рис. 1в). При наличии у
полости экваториальной плоскости симметрии достаточно рассмотреть четверть
указанного сечения (рис. 1а).
Предположим, что конечно-элементная идеализация содержит Е треугольников и G узлов, будем нумеровать узлы (вершины) треугольников 1, 2, 3 против часовой стрелки.
 |
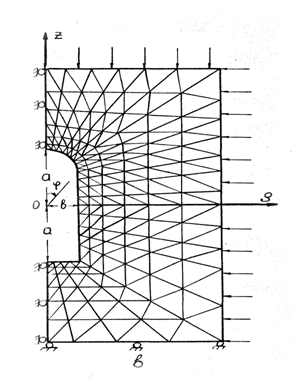 |
| Рисунок 1 – Конечно-элементная аппроксимация выделенной области с полостью | |
Для удобства дальнейшего изложения воспользуемся матричной символикой [1].
Функцию перемещений ![]() аппроксимируем
следующим образом:
аппроксимируем
следующим образом:
|
(1) |
где u, ![]() – вектора-столбцы, компоненты которых
суть проекции вектора смещений и его аппроксимации на оси координат
– вектора-столбцы, компоненты которых
суть проекции вектора смещений и его аппроксимации на оси координат ![]() , Oz;
, Oz; 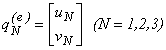 – вектор
узловых смещений е-го треугольника.
– вектор
узловых смещений е-го треугольника.
Коэффициенты ![]() определяются
через координаты узлов элемента:
определяются
через координаты узлов элемента:
 . . |
(2) |
Циклической перестановкой индексов в порядке 1, 2, 3 в (2) получаются остальные коэффициенты. Используя (1) и формулы Коши, представим вектор деформаций элемента в виде
|
(3) |
где 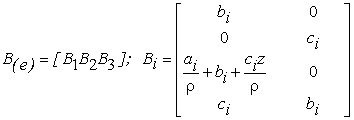 , i=1,
2, 3,
, i=1,
2, 3,
а 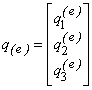 – вектор узловых
перемещений е-го элемента.
– вектор узловых
перемещений е-го элемента.
По закону Гука
|
(4) |
где 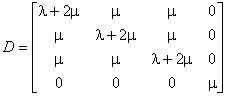 , а
, а ![]() – параметры Ламе.
– параметры Ламе.
Решение смешанной краевой задачи в случае ее осесимметричности минимизирует функционал энергии:
|
(5) |
где f, p – вектора массовых и поверхностных сил, V – область, в которой ищется решение, S – граница V. Принимая во внимание (3) и (4), получим аппроксимацию функционала (5):
|
(6) |
где матрица ![]() называется матрицей жесткости е-го конечного элемента, а матрица
называется матрицей жесткости е-го конечного элемента, а матрица
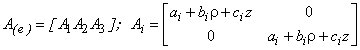 .
.
Введем матрицы ![]() размером
размером ![]() , компоненты
которых либо нуль, либо единичные. Для любого m-го
узла е-го элемента, совпадающего с i-м
узлом в глобальной нумерации узлов конечно-элементной сетки, компоненты
, компоненты
которых либо нуль, либо единичные. Для любого m-го
узла е-го элемента, совпадающего с i-м
узлом в глобальной нумерации узлов конечно-элементной сетки, компоненты ![]()
![]() и
и ![]() равны 1. После перебора всех элементов и
присвоения компонентам
равны 1. После перебора всех элементов и
присвоения компонентам ![]() единицы
согласно указанному правилу, оставшиеся компоненты приравниваются к нулю. Если
единицы
согласно указанному правилу, оставшиеся компоненты приравниваются к нулю. Если
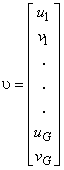
– вектор смещений узлов согласно глобальной нумерации, то
|
(7) |
Учитывая (7), запишем (6) в виде
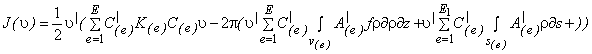
или
|
(8) |
Функционал (8) принимает минимальное значение, если  ; I =1,2,…,
; I =1,2,…,![]() .
.
Эти условия сводятся к системе линейных алгебраических уравнений относительно вектора глобальных узловых перемещений
|
(9) |
матрица
коэффициентов которой К называется матрицей жесткости системы конечных
элементов. Решение ![]() позволяет
установить деформации и напряжения по формулам (3), (4).
позволяет
установить деформации и напряжения по формулам (3), (4).
Иногда в элементах полезно задавать начальные деформации или напряжения, тогда видоизменяется связь (4), которая в этих случаях соответственно имеет вид:
|
(10) |
где ![]() и
и ![]() – начальные деформации и напряжения,
а к правой части (9) добавится слагаемое Q,
соответственно равное
– начальные деформации и напряжения,
а к правой части (9) добавится слагаемое Q,
соответственно равное
|
(11) |
или
|
(12) |
После решения
системы ![]() напряжение
вычисляются согласно (10).
напряжение
вычисляются согласно (10).
Список литературы
1. Зенкевич, О. С. Метод конечных элементов в технике / О. С. Зенкевич. – М. : Мир, 1975.
Научный электронный журнал КубГАУ . № 08(16), 2005
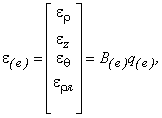
 ,
,