Научный электронный журнал КубГАУ . № 07(15), 2005
УДК 368.382
МАТЕМАТИЧЕСКОЕ И ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ПЛОТНОСТИ ВЕРОЯТНОСТИ СОСТОЯНИЙ СОЗНАНИЯ ЧЕЛОВЕКА В ЭВОЛЮЦИИ С ПРИМЕНЕНИЕМ ТЕОРИИ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Луценко Е. В. – д. э. н., к. т. н., профессор
Кубанский государственный аграрный университет
В статье предлагается математическая модель и результаты численного моделирования процессов познания и развития сознания с помощью аппарата простых однородных стационарных цепей Маркова. Обосновываются выводы о том, что путь развития сознания в процессе развития общества является наиболее массовым; для каждого этапа развития общества существует определенное наиболее массовое состояние сознания, а также менее массовые, более и менее высокие, чем наиболее массовое; кроме наиболее массового существуют и другие пути развития сознания, из-за чего с течением времени общество становится все менее однородным по уровню сознания своих членов.
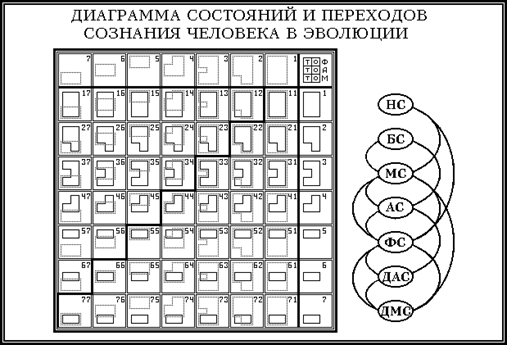
В 1979 году автором предложена периодическая классификация этапов познания при различных типах сознания, представленная в форме диаграммы состояний и переходов сознания человека в эволюции [1]:
|
Наличие классификации форм сознания открывает возможность использования для исследования процессов развития сознания математических методов, в частности, теории Марковских случайных процессов (что и было осуществлено автором в 1980 году). Естественно, для этого необходимо сделать некоторые допущения.
Постановка задачи
Случайный процесс называется Марковским, если для каждого момента времени вероятность любого состояния системы в будущем зависит только от ее состояния в настоящее время и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом). Диаграмма состояний и переходов сознания человека в эволюции содержит 28 дискретных состояний сознания, разрешенных в эволюции, переходы между которыми могут происходить, вообще говоря, как в определенные дискретные моменты времени, так и непрерывно. В первом случае процесс развития сознания описывается моделью Марковской цепи, а во втором – моделью дискретного Марковского процесса. В данной работе мы ограничимся моделью Марковской цепи, а точнее моделью простой однородной стационарной цепи Маркова [2].
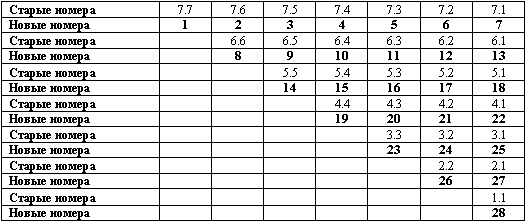
Для удобства детального анализа перенумеруем состояния сознания в диаграмме состояний и переходов сознания человека в эволюции согласно таблице.
Будем рассматривать сознание как систему С, имеющую 28 возможных
состояний: С![]() , С
, С![]() , С
, С![]() ,…, С
,…, С![]() и шаг за шагом, в определенные дискретные
моменты времени Т
и шаг за шагом, в определенные дискретные
моменты времени Т![]() <Т
<Т![]() <Т
<Т![]() ,…, Т
,…, Т![]() совершающую скачкообразные переходы С
совершающую скачкообразные переходы С![]()
![]() С
С![]() из состояний с меньшим номером в состояния с
большим номером. Будем считать также, что на каждом шаге все переходы С
из состояний с меньшим номером в состояния с
большим номером. Будем считать также, что на каждом шаге все переходы С![]()
![]() С
С![]() осуществляются с их вероятностями Р
осуществляются с их вероятностями Р![]() , и эти вероятности одношаговых
переходов от шага к шагу не меняются, т.е. постоянны и однозначно задаются
(стохастической квадратной) матрицей М
, и эти вероятности одношаговых
переходов от шага к шагу не меняются, т.е. постоянны и однозначно задаются
(стохастической квадратной) матрицей М![]() вероятностей одношаговых переходов:
вероятностей одношаговых переходов:
|
(1) |
Все элементы этой матрицы неотрицательны, а сумма элементов в каждой строке близка к единице.
Нас, прежде всего, будет интересовать решение следующей основной задачи.
Пусть известно начальное состояние С![]() сознания С и заданы вероятности Р
сознания С и заданы вероятности Р![]() одношаговых переходов С
одношаговых переходов С![]()
![]() С
С![]() из состояния С
из состояния С![]() в состояние С
в состояние С![]() . Определить вероятности Р
. Определить вероятности Р![]() переходов С
переходов С![]()
![]() С
С![]() за Т шагов, т.е. найти матрицы М
за Т шагов, т.е. найти матрицы М![]()
|
(2) |
вероятностей
Р![]() . Известно [2],
что для простой однородной цепи Маркова матрица М
. Известно [2],
что для простой однородной цепи Маркова матрица М![]() вероятностей Р
вероятностей Р![]() перехода сознания С из состояния С
перехода сознания С из состояния С![]() в состояние С
в состояние С![]() за Т шагов равна Т-й
степени матрицы М
за Т шагов равна Т-й
степени матрицы М![]() вероятностей Р
вероятностей Р![]() одношаговых переходов С
одношаговых переходов С![]()
![]() С
С![]() :
:
|
(3) |
Марковская математическая модель
Таким образом, для решения основной задачи необходимо найти
вид матрицы М![]() ,
т.е. определить вероятности Р
,
т.е. определить вероятности Р![]() одношаговых переходов между состояниями
сознания, представленными в диаграмме состояний и переходов сознания человека в
эволюции. Чтобы это сделать, рассмотрим универсальный закон переходов:
"Шаг назад – два шага вперед". Предварительно дадим необходимые
определения.
одношаговых переходов между состояниями
сознания, представленными в диаграмме состояний и переходов сознания человека в
эволюции. Чтобы это сделать, рассмотрим универсальный закон переходов:
"Шаг назад – два шага вперед". Предварительно дадим необходимые
определения.
Редуцированным состоянием сознания С называется такое состояние,
в котором сознание имеет определенный уровень развития, т.е. находится в
определенном состоянии С![]() ,
где К=константа, но имеет неопределенное направление и темп развития,
т.е. с вероятностями Р
,
где К=константа, но имеет неопределенное направление и темп развития,
т.е. с вероятностями Р![]() для него возможны все одношаговые переходы С
для него возможны все одношаговые переходы С![]()
![]() С
С![]() , где 1
, где 1![]() К<Л
К<Л![]() 28.
28.
В диаграмме состояний и переходов сознания человека в эволюции представлены только редуцированные состояния сознания.
Виртуальным состоянием сознания С называется такое состояние,
в котором сознание имеет определенное направление и темп развития, т.е.
совершает некоторый вполне определенный одношаговый переход С![]()
![]() С
С![]() (где К=константа и Л=константа), но имеет
неопределенный уровень развития, т.е. находится в неопределенном состоянии
"С
(где К=константа и Л=константа), но имеет
неопределенный уровень развития, т.е. находится в неопределенном состоянии
"С![]() " на
пути от С
" на
пути от С![]() к С
к С![]() . Однако было бы
неоправданным упрощением представление о том, что Н "очень быстро"
пробегает все промежуточные значения от К до Л и в буквальном смысле находится
где-то между ними, т.е. что К<Н<Л. В действительности переход С
. Однако было бы
неоправданным упрощением представление о том, что Н "очень быстро"
пробегает все промежуточные значения от К до Л и в буквальном смысле находится
где-то между ними, т.е. что К<Н<Л. В действительности переход С![]()
![]() С
С![]() совершается по диалектическим законам, и, в
частности, по закону отрицания-отрицания, следовательно, в этом переходе
отражаются некоторые (но не все) черты редуцированного состояния С
совершается по диалектическим законам, и, в
частности, по закону отрицания-отрицания, следовательно, в этом переходе
отражаются некоторые (но не все) черты редуцированного состояния С![]() , которое настолько же
отстоит от состояния С
, которое настолько же
отстоит от состояния С![]() назад, насколько состояние С
назад, насколько состояние С![]() отстоит от него вперед. В этом и состоит
смысл универсального закона переходов сознания в эволюции. Сформулируем этот
закон более подробно.
отстоит от него вперед. В этом и состоит
смысл универсального закона переходов сознания в эволюции. Сформулируем этот
закон более подробно.
Пусть совершается одношаговый переход С![]()
![]() С
С![]() (без промежуточных редуцированных состояний)
сознания С из редуцированного состояния С
(без промежуточных редуцированных состояний)
сознания С из редуцированного состояния С![]() в редуцированное состояние С
в редуцированное состояние С![]() . Величина шага Ш равна:
. Величина шага Ш равна:
|
(4) |
Виртуальное состояние "С![]() " представляет собой непосредственно сам
переход между редуцированными состояниями С
" представляет собой непосредственно сам
переход между редуцированными состояниями С![]() и С
и С![]() . Сознание С сначала переходит из
редуцированного состояния С
. Сознание С сначала переходит из
редуцированного состояния С![]() в виртуальное состояние "С
в виртуальное состояние "С![]() ", подобное по закону
отрицания-отрицания редуцированному состоянию С
", подобное по закону
отрицания-отрицания редуцированному состоянию С![]() , отстоящему от редуцированного состояния С
, отстоящему от редуцированного состояния С![]() на один шаг назад:
на один шаг назад:
|
(5) |
а
затем из виртуального состояния "С![]() " переходит в реальное состояние С
" переходит в реальное состояние С![]() , совершая при этом два
шага вперед:
, совершая при этом два
шага вперед:
|
(6) |
Таким образом, универсальный закон переходов "шаг назад – два шага вперед" рассматривает диалектику одношаговых переходов и может быть наглядно представлен в виде простейшего графа:
|
(7) |
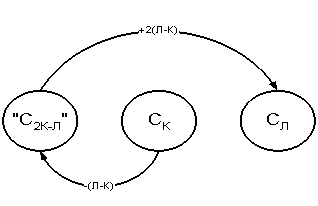
Заметим, что в процессе развития сознания редуцированные и виртуальные состояния сознания чередуются подобно тому, как они чередуются в процессе движения элементарной частицы [1]. Диаграмма состояний и переходов сознания человека в эволюции по существу отображает дискретное фазовое пространство состояний и развития сознания. Некоторые из переходов сознания человека в эволюции, построенные на основе универсального закона переходов "Шаг назад – два шага вперед", символически отображены на диаграмме состояний и переходов сознания человека в эволюции в виде графов, построенных, соответственно, на основе графа (7).
Переход С![]()
![]() С
С![]() называется одношаговым, если он совершается
без промежуточных редуцированных состояний. Путь развития сознания есть такая
последовательность одношаговых переходов, в которой редуцированное состояние –
конец каждого предыдущего перехода – представляет собой в то же время начало
последующего перехода. Существует большое количество различных путей, ведущих
от одного редуцированного состояния сознания к другому.
называется одношаговым, если он совершается
без промежуточных редуцированных состояний. Путь развития сознания есть такая
последовательность одношаговых переходов, в которой редуцированное состояние –
конец каждого предыдущего перехода – представляет собой в то же время начало
последующего перехода. Существует большое количество различных путей, ведущих
от одного редуцированного состояния сознания к другому.
Получим выражение для числа путей П![]() перехода С
перехода С![]()
![]() С
С![]() , где 1
, где 1![]() К<Л
К<Л![]() 28. Для этого необходимо найти связь между П
28. Для этого необходимо найти связь между П![]() и П
и П![]() , а также между П
, а также между П![]() и П
и П![]() .
.
От С![]() к С
к С![]() ведут как
все те же пути, что и от С
ведут как
все те же пути, что и от С![]() к С
к С![]() , но завершающиеся переходом С
, но завершающиеся переходом С![]()
![]() С
С![]() , так и все те же пути, что и от С
, так и все те же пути, что и от С![]() к С
к С![]() , но завершающиеся переходом С
, но завершающиеся переходом С![]()
![]() С
С![]() , где 1
, где 1![]() К
К![]() Р<Л–1
Р<Л–1![]() 27, т.е.:
27, т.е.:
|
(8) |
С другой стороны, от С![]() к С
к С![]() ведут как все те же пути, что и от С
ведут как все те же пути, что и от С![]() к С
к С![]() , но начинающиеся переходом С
, но начинающиеся переходом С![]()
![]() С
С![]() , так и те же пути, что и от С
, так и те же пути, что и от С![]() к С
к С![]() , но начинающиеся переходом С
, но начинающиеся переходом С![]()
![]() С
С![]() , где 2
, где 2![]() К+1<Р
К+1<Р![]() Л
Л![]() 28, т.е.:
28, т.е.:
|
(9) |
Положим, в выражении (8) Л=К+2, тогда получим:
|
(10) |
Переход С![]()
![]() С
С![]() является одношаговым, и, следовательно, существует
единственный путь этого перехода:
является одношаговым, и, следовательно, существует
единственный путь этого перехода:
|
(11) |
Далее последовательным применением рекуррентного соотношения (8) получим:
|
(12) |
Откуда В=Л–К и
|
(13) |
при 1![]() К<Л
К<Л![]() 28.
28.
Так как возможны только те переходы С![]()
![]() С
С![]() , для которых 1
, для которых 1![]() К<Л<28, то
К<Л<28, то
|
(14) |
при К![]() Л.
Объединяя выражения (13) и (14) получим:
Л.
Объединяя выражения (13) и (14) получим:
|
(15) |
Пользуясь выражением (15), определим вероятности Р![]() одношаговых переходов С
одношаговых переходов С![]()
![]() С
С![]() сознания С из состояния С
сознания С из состояния С![]() в состояние С
в состояние С![]() . Будем считать, что если сознание
С исходит из состояния С
. Будем считать, что если сознание
С исходит из состояния С![]() и стремится как к цели к состоянию С
и стремится как к цели к состоянию С![]() , то вероятность Р
, то вероятность Р![]() одношагового перехода С
одношагового перехода С![]()
![]() С
С![]() в некоторое состояние С
в некоторое состояние С![]() равно отношению П
равно отношению П![]() /П
/П![]() числа путей П
числа путей П![]() перехода С
перехода С![]()
![]() С
С![]() к числу путей П
к числу путей П![]() перехода С
перехода С![]()
![]() С
С![]() :
:
|
(16) |
Это определение вероятности Р![]() связано с мерой целесообразности информации,
которая определяется А. А. Харкевичем как изменение вероятности достижения цели
при получении дополнительной информации [4].
связано с мерой целесообразности информации,
которая определяется А. А. Харкевичем как изменение вероятности достижения цели
при получении дополнительной информации [4].
В определении (16) вероятности Р![]() одношагового перехода С
одношагового перехода С![]()
![]() С
С![]() число путей П
число путей П![]() перехода С
перехода С![]()
![]() С
С![]() , очевидно, не должно быть равным нулю:
, очевидно, не должно быть равным нулю:
|
(17) |
Но так как согласно выражению (15) это возможно только при
К<М, а 1![]() К
К![]() 27, то очевидно, что
условие (17) осуществляется для всех К только при М=28. Используя в (16)
выражение (15) получим:
27, то очевидно, что
условие (17) осуществляется для всех К только при М=28. Используя в (16)
выражение (15) получим:
-
при 1![]() К<Л
К<Л![]() М=28
М=28
|
(18) |
-
при К![]() Л
Л
|
(19) |
Итак,
|
(20) |
Выражение (20) полностью определяет все элементы матрицы М![]() :
:
|
(1) |
вероятностей
одношаговых переходов. Примечательно, что вероятность Р![]() зависит только от разности
аргументов (Л–К), что полностью соответствует определению однородной Марковской
цепи [2].
зависит только от разности
аргументов (Л–К), что полностью соответствует определению однородной Марковской
цепи [2].
Определим вероятности Р![]() и количества путей П
и количества путей П![]() перехода С
перехода С![]()
![]() С
С![]() сознания С из состояния С
сознания С из состояния С![]() в состояние С
в состояние С![]() за Т шагов. Последовательно
полагая в выражении (3) Т=2,3,4,…,27 и применяя правила перемножения матриц,
получаем для определения вероятностей Р
за Т шагов. Последовательно
полагая в выражении (3) Т=2,3,4,…,27 и применяя правила перемножения матриц,
получаем для определения вероятностей Р![]() рекуррентную формулу:
рекуррентную формулу:
|
(21) |
где Т=2,3,4,…,27.
Представим Р![]() в виде:
в виде:
|
(22) |
где коэффициенты П![]() определяются следующим образом:
определяются следующим образом:
|
(23) |
Выражение (23) полностью определяет матрицу П![]() коэффициентов П
коэффициентов П![]() :
:
|
(24) |
Положим в выражении (21) Т=2 и подставим в него Р![]() из (22), тогда получим:
из (22), тогда получим:
|
(25) |
где
|
(26) |
и, следовательно,
|
(27) |
Далее, полагая в выражении (21) Т=3 и подставляя в него Р![]() из (22) и Р
из (22) и Р![]() из (25), получим:
из (25), получим:
|
(28) |
где
|
(29) |
и
|
(30) |
Если в (30) использовать (27), то получим:
|
(31) |
Итак, из сравнения выражений (22), (25) и (28) мы видим, что
вероятности Р![]() перехода С
перехода С![]()
![]() С
С![]() сознания С из состояния С
сознания С из состояния С![]() в состояние С
в состояние С![]() за Т шагов могут быть
представлены в виде:
за Т шагов могут быть
представлены в виде:
|
(32) |
где коэффициенты П![]() определяются из рекуррентного соотношения:
определяются из рекуррентного соотношения:
|
(33) |
и представляют собой элементы матриц П![]() :
:
|
(34) |
При получении выражений (33) и (34) использованы формулы (26), (29) и (27), (31) соответственно.
Рассмотрим выражение (33). Его можно представить в виде:
|
(35) |
Но согласно (23) все П![]() в первой сумме выражения (35) равны единице,
а во второй нулю, поэтому выражение (35) принимает вид:
в первой сумме выражения (35) равны единице,
а во второй нулю, поэтому выражение (35) принимает вид:
|
(36) |
Замечаем [3], что выражению (36) удовлетворяют элементы треугольника Паскаля, определяемые по формуле:
|
(37) |
где: 1![]() К<Л
К<Л![]() 28; 1
28; 1![]() Т
Т![]() Л–К.
Л–К.
Используя выражение (37) для П![]() в (32), окончательно для Р
в (32), окончательно для Р![]() получим:
получим:
|
(38) |
Заменяя в (37) и (38) факториалы гамма-функциями, получаем обобщения этих выражений для непрерывного случая, более удобные для численных расчетов и построения графиков:
|
(37*) |
|
(38*) |
где М=Л–К.
Выражение (38) определяет вероятность Р![]() перехода С
перехода С![]()
![]() С
С![]() сознания С из состояния С
сознания С из состояния С![]() в состояние С
в состояние С![]() за Т шагов и представляет собой
основной итог данной работы. По сути, выражение (38*) определяет
плотность вероятности нахождения сознания в различных состояниях в зависимости
от времени, а значит, может быть названо "Динамическим распределением форм
сознания в эволюции".
за Т шагов и представляет собой
основной итог данной работы. По сути, выражение (38*) определяет
плотность вероятности нахождения сознания в различных состояниях в зависимости
от времени, а значит, может быть названо "Динамическим распределением форм
сознания в эволюции".
В полном соответствии с определением однородной цепи Маркова [2]
вероятности Р![]() ,
определяемые выражением (38), зависят только от разности (Л–К) аргументов
"Л" и "К" начального и конечного состояний перехода С
,
определяемые выражением (38), зависят только от разности (Л–К) аргументов
"Л" и "К" начального и конечного состояний перехода С![]()
![]() С
С![]() и не зависят от пути этого перехода. Из
этого, а также из соотношения
и не зависят от пути этого перехода. Из
этого, а также из соотношения
|
(39) |
справедливость
которого легко установить непосредственно используя выражения (37) и (15),
следует, что П![]() представляет собой количество путей перехода С
представляет собой количество путей перехода С![]()
![]() С
С![]() за Т шагов (41,16), а 2
за Т шагов (41,16), а 2![]() есть вероятность любого из путей
этого перехода в отдельности. Следовательно, преимущества одного пути
эволюции перед другим (в смысле его большей вероятности) в рамках модели
простой (одномерной) цепи Маркова установить невозможно. Для решения этой
важнейшей задачи необходимо использование более общей модели сложных цепей Маркова [2], в которых вероятность перехода С
есть вероятность любого из путей
этого перехода в отдельности. Следовательно, преимущества одного пути
эволюции перед другим (в смысле его большей вероятности) в рамках модели
простой (одномерной) цепи Маркова установить невозможно. Для решения этой
важнейшей задачи необходимо использование более общей модели сложных цепей Маркова [2], в которых вероятность перехода С![]()
![]() С
С![]() зависит от пути, по которому система пришла
в состояние С
зависит от пути, по которому система пришла
в состояние С![]() , а
точнее, зависит от М состояний системы, непосредственно предшествующих
состоянию С
, а
точнее, зависит от М состояний системы, непосредственно предшествующих
состоянию С![]() , где
М>1.
, где
М>1.
Однако уже модель простой однородной цепи Маркова позволяет
изучить динамику населенности различных состояний сознания в процессе эволюции.
Для этого необходимо (используя выражение (38)) произвести вычисление
вероятностей Р![]() для всех 1
для всех 1![]() Т
Т![]() Л–К
Л–К![]() 27.
27.
Заметим также, что числа П![]() называются треугольными, т.к. они указывают
количества шаров, которые можно уложить в виде треугольника, а числа П
называются треугольными, т.к. они указывают
количества шаров, которые можно уложить в виде треугольника, а числа П![]() – тетраэдрическими, т.к.
эти числа показывают, сколько шаров могут быть уложены в виде треугольной
пирамиды-тетраэдра [3]. Эти названия дали им еще в 5 в. до н. э. пифагорейцы,
которые изучали числа П
– тетраэдрическими, т.к.
эти числа показывают, сколько шаров могут быть уложены в виде треугольной
пирамиды-тетраэдра [3]. Эти названия дали им еще в 5 в. до н. э. пифагорейцы,
которые изучали числа П![]() ,
придавая им мистический смысл, возможно, связанный по закону отрицания-отрицания
с тем научным смыслом, который придаем этим числам мы.
,
придавая им мистический смысл, возможно, связанный по закону отрицания-отрицания
с тем научным смыслом, который придаем этим числам мы.
Результаты численного моделирования
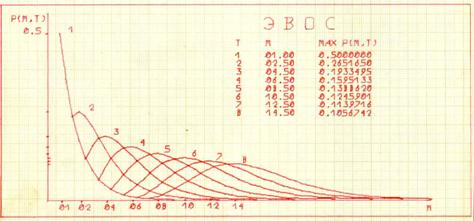
В 1983 году у автора впервые появилась возможность численно просчитать кривые плотности вероятности состояний сознания в эволюции в зависимости от времени в соответствии с выражением (38*) на компьютере Wang-2200C. Полученные кривые, выведенные на графопостроителе, приведены ниже.
|
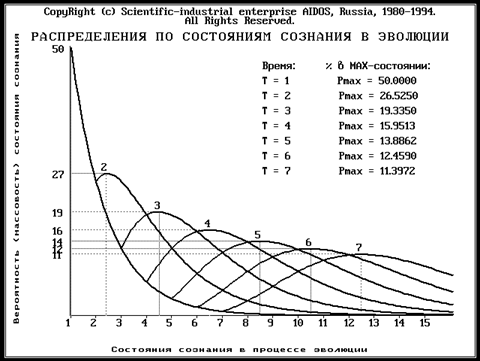
В 1994 году эти же кривые были просчитаны автором на ИБМ – совместимом персональном компьютере (графики и исходный текст программы на языке xBase приведены ниже).
|
Исходный тест программы для численного моделирования на языке xBase:
***********************************************************************
*** ЛУЦЕНКО Е.В. ВЕРОЯТНОСТИ СОСТОЯНИЙ СОЗНАНИЯ В ЭВОЛЮЦИИ 27.11.1994
***********************************************************************
#include "BI_2D.CH"
#include "BI_3D.CH"
#include "BI_FONT.CH"
#include "BI_GEGA.CH"
#include "BI_MENU.CH"
#include "BI_MOUSE.CH"
#include "BI_PCX.CH"
#include "BI_PRN.CH"
#include "BI_STD.CH"
#include "BI_SWAP.CH"
SET DECIMALS TO 15
PUBLIC Disk_name := DISKNAME()
PUBLIC Cur_dir := CURDIR()
PUBLIC Disk_dir := Disk_name+":\"+Cur_dir
PUBLIC FNT_dir := Disk_dir+"\FNT\"
******************************************************************************
*** -м ***
*** Г(м) * 2 ***
*** Р(м,т) = ----------------- ***
*** Г(т) * Г(м-т+1) ***
*** ***
*** где: Р(м,т) - вероятность состояния "м" в момент времени "т"; ***
*** Г() - гамма - функция. ***
******************************************************************************
G_buf=SAVESCREEN(0,0,24,79)
Min_x = 0
Max_x = 15
Sh = 0.1
Min_y = 0
PRIVATE xdata[Max_x/Sh], ydata[Max_x/Sh]
// Инициализация системы BiGraph 3.0/2D
InitGraphics2D(VGA_640x480)
// Установка активности окна
SetCurrentWindow(1)
// Задание "фона" в окне
SetViewBackground(WHITE)
// Задание цвета рамки-окантовки графика
BorderCurrentWindow(BLACK)
// Задание цвета "фона" внутренней области
SetPlotBackground(WHITE)
// Вывод осей и рисок
Set_FrColor(BLACK)
Draw_LineAB(87,56,87,414,BLACK)
Draw_LineAB(87,414,88+508,414,BLACK)
Load_ABCfont(Fnt_dir+"F16.fnt",0);Set_ABCcolor(BLACK,0)
FOR j=1 TO Max_x
X1 = 88+(j-1)*506/Max_x
Draw_LineAB(X1,414,X1,417,BLACK)
Set_ABCxy(X1,422,0);String_ABC(ALLTRIM(STR(j,2)),0)
NEXT
// Надписи по осям координат
Set_FrColor(BLACK)
TitleXAxis("Состояния сознания в процессе эволюции")
TitleYAxis("Вероятность (массовость) состояния сознания")
Load_ABCfont(Fnt_dir+"F16.fnt",0);Set_ABCcolor(BLACK,0)
String = "CopyRight (c) Scientific-industrial enterprise AIDOS, Russia, 1980-1994."
Set_ABCxy(INT((640-Get_ABCstr(String,0))/2),08,0);String_ABC(String,0)
String = "All Rights Reserved."
Set_ABCxy(INT((640-Get_ABCstr(String,0))/2),20,0);String_ABC(String,0)
Load_ABCfont(Fnt_dir+"N24f.fnt",0);Set_ABCcolor(BLACK,0)
String = "РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ СОЗНАНИЯ В ЭВОЛЮЦИИ"
Set_ABCxy(INT((640-Get_ABCstr(String,0))/2),35,0);String_ABC(String,0)
Time = 7
PRIVATE Maxv[Time],Maxx[Time],Maxy[Time]
AFILL(Maxv,-999999);AFILL(Maxx,0);AFILL(Maxy,0)
Load_ABCfont(Fnt_dir+"F16.fnt",0);Set_ABCcolor(BLACK,0)
K = 506 / Max_x
FOR t = 1 TO Time
FOR m=t TO 1+Max_x STEP Sh
Pmt = P(m,t)
X1 = 88+(m-1)*K
Y1 = 414-712*Pmt
X2 = 88+(m-1+Sh)*K
Y2 = 414-712*P(m+Sh,t)
IF Pmt > Maxv[t]
Maxv[t] = Pmt
Maxx[t] = X1
Maxy[t] = Y1
ENDIF
NEXT
Draw_LineAB(Maxx[t],Maxy[t],Maxx[t],414,LIGHT_GRAY)
Set_ABCxy(70,Maxy[t],0);String_ABC(ALLTRIM(STR(Maxv[t]*100,2)),0)
Draw_LineAB(Maxx[t],Maxy[t],88,Maxy[t],LIGHT_GRAY)
IF t > 1
Set_ABCxy(Maxx[t],Maxy[t]-10,0);String_ABC(ALLTRIM(STR(t,2)),0)
ENDIF
NEXT
Load_ABCfont(Fnt_dir+"F16.fnt",0);Set_ABCcolor(BLACK,0)
String = "Время: % в МАХ-состоянии:"
Set_ABCxy(350,80,0);String_ABC(String,0)
K = 506 / Max_x
FOR t = 1 TO Time
FOR m=t TO 1+Max_x STEP Sh
Pmt = P(m,t)
X1 = 88+(m-1)*K
Y1 = 414-712*Pmt
X2 = 88+(m-1+Sh)*K
Y2 = 414-712*P(m+Sh,t)
Draw_LineAB(X1,Y1,X2,Y2,BLACK)
Draw_LineAB(X1,Y1+1,X2,Y2+1,BLACK)
Draw_LineAB(X1+1,Y1,X2+1,Y2,BLACK)
IF Pmt > Maxv[t]
Maxv[t] = Pmt
Maxx[t] = X1
Maxy[t] = Y1
ENDIF
NEXT
String = "T = "+ALLTRIM(STR(t,4))+" Pmax = "+ALLTRIM(STR(Maxv[t]*100,8,4))
Set_ABCxy(350,100+(t-1)*20,0);String_ABC(String,0)
NEXT
INKEY(0)
Save_PCX("Pic_09.pcx",480)
Free_ABCfont(0)
Set_TextMode()
RESTSCREEN(0,0,24,79,G_buf)
QUIT
***************** ВЫЧИСЛЕНИЕ ГАММА-ФУНКЦИИ **********************************
FUNCTION GAMMA(X)
P = 3.141592653589793
D = 1
B = ABS(X)
DO WHILE B > 1
D = D * B
B = B - 1
ENDDO
F = (( 0.035868343 * B - 0.193527818 ) * B + 0.482199394 ) * B
F = ((( F - 0.756704078 ) * B + 0.918206857 ) * B - 0.897056937 ) * B
F = (( F + 0.988205891 ) * B - 0.577191652 ) * B + 1
G = F * D / X
IF X > 0
RETURN(G)
ENDIF
G = P / SIN( P * X ) / D / F
RETURN(G)
******************* ВЫЧИСЛЕНИЕ ФУНКЦИИ P(m,t) ********************************
FUNCTION P(m,t)
RETURN(( GAMMA(m) * 2^(-m) ) / ( GAMMA(t) * GAMMA(m-t+1) ))
************ THE END ************************************
Ограничения предложенной модели и перспективы ее развития
Предложенная математическая модель является упрощенной и не отражает, например, следующее:
- динамику промежуточных состояний, т.е. явлений накопления людей на рубежах перехода к следующим типам сознания и диффузии через эти барьеры (А. А. Босенко, 1984);
- возможных зависимостей вероятностей переходов в различные формы сознания от пути, по которому человек оказался в данном состоянии, а не только от самого состояния (составные цепи Маркова);
- сама матрица вероятностей переходов также скорее всего является функцией времени, причем функцией, зависящей от места на планете или в космосе;
- матрица вероятностей переходов может быть детализирована за счет увеличения ее размерности и количества классифицированных редуцированных состояний сознания, и т.д., и т.д.
Решение этих и других вопросов представляет перспективу дальнейших исследований.
Выводы:
1. Путь развития сознания в процессе развития общества является наиболее массовым.
2. Для каждого этапа развития общества существует определенное наиболее массовое состояние сознания.
3. Существование других путей развития сознания приводит к "размыванию" основного максимума с течением времени, т.е. к тому, что общество становится все более неоднородным по уровню сознания своих членов.
Список литературы
1. Луценко, Е. В. Опыт исследования высших форм сознания / Е. В. Луценко // Высшие формы сознания – высшие технологии [Электронный ресурс]. – Краснодар, 2005. – Режим доступа: http://lc.kubagro.ru/master/index.htm.
2. Тихонов, В. И. Марковские процессы / В. И.Тихонов, М. А. Миронов. – М., 1977.
3. Успенский, В. А. Треугольник Паскаля / В. А. Успенский. – М., 1979.
4. Темников, Ф. Е. Теоретические основы информационной техники / Ф. Е. Темников, В. А. Афонин, В. И. Дмитриев. – М. : "Энергия", 1979. – С. 56–57.
Научный электронный журнал КубГАУ . № 07(15), 2005
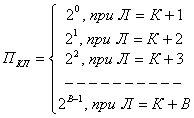 .
.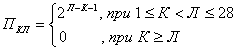 .
.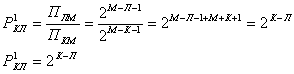 ;
;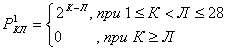 .
.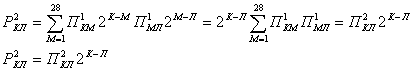 ,
,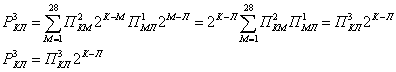 ,
,