Научный электронный журнал КубГАУ . № 02(10), 2005
МЕТОДИКА И МОДЕЛИ ОПТИМИЗАЦИИ ВХОДНЫХ ПАРАМЕТРОВ ТЕХНОЛОГИЧЕСКОЙ ЦЕПИ ХЛЕБОПРОДУКТОВОГО ОБЪЕДИНЕНИЯ
Лойко В.И. – д.т.н., профессор
Кубанский государственный аграрный университет
Першакова Т.В. – к. т. н., доцент
Ищенко О.В. – старший преподаватель
Краснодарский кооперативный институт (филиал БУПК)
В статье предлагается методика и модели оптимизации входных параметров технологической цепи хлебопродуктового объединения потребительской кооперации.
Рассмотрим наиболее типичные вертикально интегрированные структуры хлебопродуктовых объединений потребительской кооперации (рис. 1, 5 в [1]).
Годовой объем необходимого сырья для переработки, а значит и годовой объем финансовых средств для закупки может быть рассчитан, исходя из годового спроса на хлебопекарную продукцию сегмента рынка потребительской кооперации. Если сразу закупить (или произвести) годовой объем исходного продукта переработки (в [1] для структуры рис. 5 это зерно, а для структуры рис. 1 – мука), то за год будет реализован всего один цикл. В этом случае сразу возникает почти неразрешимая проблема (как финансовая, так и складская) хранения такого большого объема запасов. Если же производить закупки мелкими партиями (большое число циклов в году), проблемой станут резко увеличившиеся затраты, связанные с частыми заказами (документация, транспортировка, погрузочно-разгрузочные работы и т.п.).
Таким образом, возникает задача оптимизации числа циклов m и связанных с
ним объемов финансового ![]() и материального
и материального ![]() потоков.
потоков.
Как указывалось в [1], число циклов может быть определено по количеству
поставок исходного для производства сырья в течение года. Для закупки и
организации поставки необходимо возникновение исходного финансового потока ![]() , компенсирующего произведенные начальные издержки и, таким образом,
запускающего производственный цикл вертикально интегрированной системы.
, компенсирующего произведенные начальные издержки и, таким образом,
запускающего производственный цикл вертикально интегрированной системы.
Для бесперебойного
функционирования технологической цепи необходимо, чтобы на входе каждого ее
звена в любой производственный момент времени находилось достаточное количество
исходного для переработки сырья или, другими словами, запасов. Поскольку
производственные запасы в течение технологического процесса расходуются, то их
необходимо возобновлять. С этой целью вновь создается финансовый поток ![]() , инициирующий возобновление уменьшившихся до минимального уровня
производственных запасов, и так далее. Возникают типичные производственные
циклы, причем их длительность и количество прямо связаны со скоростью расходования
созданных в начале цикла запасов.
, инициирующий возобновление уменьшившихся до минимального уровня
производственных запасов, и так далее. Возникают типичные производственные
циклы, причем их длительность и количество прямо связаны со скоростью расходования
созданных в начале цикла запасов.
В связи с вышесказанным
воспользуемся для определения числа циклов m и объемов исходных финансового ![]() и материального
и материального ![]() потоков
в вертикально интегрированной хлебопродуктовой производственной системе теорией
управления запасами [3].
потоков
в вертикально интегрированной хлебопродуктовой производственной системе теорией
управления запасами [3].
Необходимость запасов объясняется случайными процессами, протекающими в производственных системах. Нельзя быть уверенным в том, что продукты для переработки поступят на склад технологического звена именно в тот момент времени, когда они понадобятся. Если на некоторой стадии процесса производства потребуется какой-то вид сырья, а этого сырья не окажется в запасе, т. е. образовался дефицит, то процесс производства может задержаться или вообще остановиться.
Очевидно, что таких ситуаций необходимо по возможности избегать: на складах технологических звеньев (предприятий) хлебопродуктового объединения всегда должно быть нужное количество данного вида сырья. Однако если запасы увеличить, соответственно возрастет плата за их хранение. Управление запасами состоит в том, чтобы выбрать компромиссное или даже оптимальное решение при определенных условиях или ограничениях.
Независимо от того, какого рода систему управления запасами имеет производство, основные решения, которые может принять управляющий орган, состоят в следующем [3]:
- какое количество товара должно находиться в запасе;
- в какое время производить пополнение запаса.
Предметом исследования является связь между
количеством Q запаса, имеющегося на складе производственного звена
технологической цепи, и временем t, для которого
рассматривается этот запас. Таким образом, мы исследуем функцию ![]() , соответствующую величине запаса в момент времени t. Под Q будем понимать запасы только одного вида.
, соответствующую величине запаса в момент времени t. Под Q будем понимать запасы только одного вида.
1. Модель для идеальных условий
Согласно классической модели Харриса, рассматривается непрерывное расходование запасов и мгновенное их поступление.
На рисунке 1 показан пример графика изменения запасов для такой модели.
В течение длительности цикла T идет расходование запаса, и в момент спада запасов до нуля происходит их восстановление до уровня q. Этот момент называют "точкой заказа", положение которой определяет длительность цикла.

Рисунок 1 – График изменения запасов в модели Харриса
В системах управления запасами основными вопросами являются состав и размеры издержек управления.
Рассматриваемые в модели величины, их обозначения, а также принятые относительно этих величин допущения представлены в таблице 1.
|
Величина |
Обозначение |
Единицы |
Допущения |
|
Интенсивность спроса |
a |
Единицы товара в год |
Спрос постоянен и непрерывен |
|
Организационные издержки |
S |
Рублей за одну партию |
Организационные издержки постоянны |
|
Стоимость подлежащего переработке продукта |
c |
Рублей за |
Цена единицы |
|
Издержки содержания запасов |
h |
Рублей за единицу товара в год |
Стоимость |
|
Размер партии поставки |
q |
Единицы товара в год |
Постоянная |
Рассмотрим ситуации, в которых издержки, связанные с запасами, могут быть объяснены независимо друг от друга.
1. Организационные издержки – расходы, связанные с оформлением и доставкой подлежащего переработке продукта (товара), необходимые для каждого цикла складирования. Эти затраты связаны с подготовительно-заключительными операциями при поступлении сырья и подаче заявок.
2. Издержки содержания запасов – затраты, связанные с хранением и амортизацией в процессе хранения (товары могут портиться, устаревать, их количество может уменьшаться и т.п.).
3. Издержки, связанные с дефицитом, – поставка не может быть выполнена, это допускается в моделях с дефицитом, что приводит к дополнительным издержкам, обусловленным отказом.
Уравнение издержек С, связанных с запасами, сделанными в течение года, может быть записано в соответствии с таблицей 1 следующим образом:
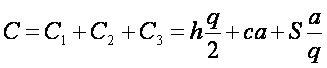 , (1)
, (1)
где 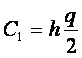 – общие издержки содержания запасов;
– общие издержки содержания запасов;
![]() – стоимость товара;
– стоимость товара;
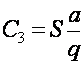 – общие организационные издержки.
– общие организационные издержки.
На рисунке 2 показан приближенный
график функции ![]() , отвечающий формуле (1).
, отвечающий формуле (1).
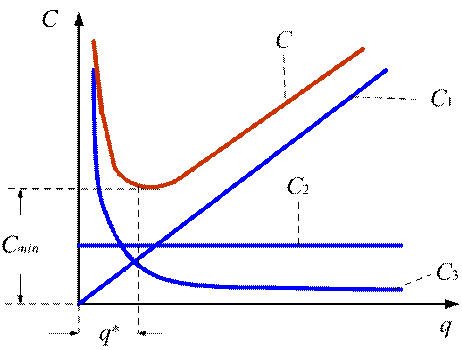
Рисунок 2 – График изменения издержек
Чтобы найти значение партии
поставки, обращающее С в минимум, используем необходимое условие экстремума 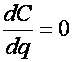 . Это действительно точка минимума, так как
. Это действительно точка минимума, так как 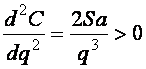 .
.
Следовательно, справедливо:
![]()
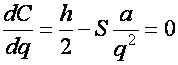 . (2)
. (2)
Решая последнее уравнение
относительно q, найдем оптимальный размер партии поставки q*, а значит и оптимальный объем
исходного материального потока ![]() :
:
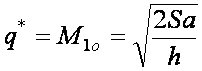 . (3)
. (3)
Величина q* называется оптимальным размером партии поставки товарного запаса. Уравнение (3) иногда называют формулой оптимального заказа.
Чтобы полностью удовлетворить годовой спрос a при размере поставки, равном q*, необходимо сделать a/q* поставок за год.
Таким образом, число циклов m технологической цепи в течение года можно определить как:
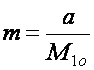 , (4)
, (4)
где a – годовая потребность в сырье для переработки;
![]() – оптимальный объем исходного
материального потока, вычисляемый по формуле (3).
– оптимальный объем исходного
материального потока, вычисляемый по формуле (3).
Если подставить вместо объема исходного
материального потока ![]() в
формуле (4) его выражение из (3), получим оптимальное число циклов
в
формуле (4) его выражение из (3), получим оптимальное число циклов ![]() :
:
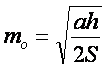 . (5)
. (5)
Минимальный объем финансового потока ![]() , запускающего технологический цикл, определим по типу соотношения (1), в
котором учтем, что рассматривается один цикл, а значит, и один оптимальный по объему
материальный поток
, запускающего технологический цикл, определим по типу соотношения (1), в
котором учтем, что рассматривается один цикл, а значит, и один оптимальный по объему
материальный поток ![]() :
:
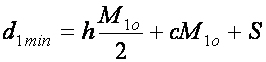 . (6)
. (6)
Если подставить в (4) выражение ![]() из (3), получим соотношение для расчета минимального объема финансового
потока
из (3), получим соотношение для расчета минимального объема финансового
потока ![]() , зависящее
только от параметров поставок и хранения сырья:
, зависящее
только от параметров поставок и хранения сырья:
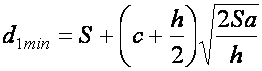 . (7)
. (7)
2. Модель для производственных условий
В реальных производственных условиях, во-первых, не может быть мгновенных поставок партий исходного продукта переработки, а во-вторых, технологический процесс, как правило, является непрерывным, и в течение выполнения с определенной скоростью р поставки сырья происходит его потребление, тоже с определенной скоростью a. Причем очевидно, что скорость поставки сырья должна превышать скорость его потребления ( р > a ).
Задача управления запасами в этих условиях может
быть сформулирована практически так же, как и предыдущая задача, с тем
отличием, что поставки партий сырья на склад производятся не мгновенно, а
равномерно в течение определенного промежутка времени ![]() , т.е. задана и скорость поставки р (рис. 3).
, т.е. задана и скорость поставки р (рис. 3).
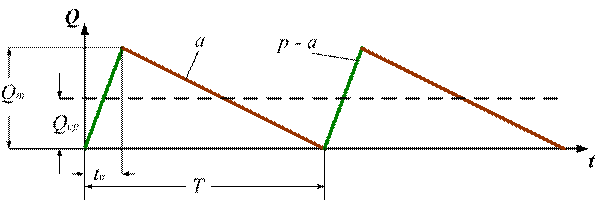
Рисунок 3 – График изменения запасов в производственных условиях
Допущения здесь те же, что и в задаче Харриса, кроме дополнительного, которое формулируется так:
при уменьшении запасов на складе до нуля начинаются поставки и продолжаются до тех пор, пока не будет поставлена одна партия. При этом отгрузка поставляемого сырья для осуществления технологического процесса не прекращается.
Суммарные издержки в заданной системе могут быть записаны в виде:
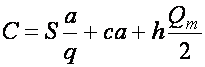 , (8)
, (8)
где ![]() – максимальный
уровень запасов на складе.
– максимальный
уровень запасов на складе.
Уровень запасов ![]() ,
для размещения которого должны быть подготовлены складские помещения, может
быть определен как произведение длительности поставки сырья
,
для размещения которого должны быть подготовлены складские помещения, может
быть определен как произведение длительности поставки сырья ![]() и разности скоростей его поставки р и отгрузки d:
и разности скоростей его поставки р и отгрузки d:
![]() . (9)
. (9)
Размер партии поставки определяется как произведение скорости поставки и ее длительности:
![]() .
.
Следовательно,
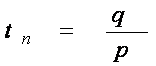 . (10)
. (10)
Подставив значение ![]() из
(10) в формулу (9), получим для
из
(10) в формулу (9), получим для ![]() :
:
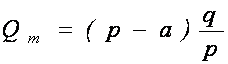 . (11)
. (11)
А выражение для издержек после подстановки (8) приобретет вид:
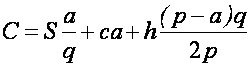 . (12)
. (12)
Продифференцировав C по q и приравняв производную нулю, получим формулу для оптимального размера партии поставки и объема исходного материального потока:
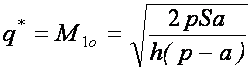 . (13)
. (13)
Чтобы полностью удовлетворить годовой спрос при оптимальном объеме исходного материального потока, необходимо осуществить число циклов, равное
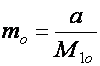 , (14)
, (14)
Если подставить вместо оптимального объема исходного материального потока в формуле (14) его выражение из (13), получим:
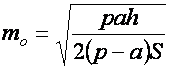 . (15)
. (15)
Минимальный объем финансового потока ![]() , запускающего технологический цикл, определим по типу соотношения (12),
в котором учтем, что рассматривается один цикл, а значит, и один оптимальный по
объему материальный поток
, запускающего технологический цикл, определим по типу соотношения (12),
в котором учтем, что рассматривается один цикл, а значит, и один оптимальный по
объему материальный поток ![]() :
:
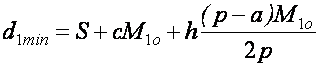 . (16)
. (16)
Подставив в (16) соотношение для ![]() из (13), получим:
из (13), получим:
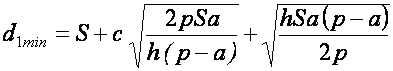 . (17)
. (17)
Оптимальные длительность поставки ![]() и пиковый объем поставляемого сырья
и пиковый объем поставляемого сырья ![]() будут
определяться по формулам:
будут
определяться по формулам:
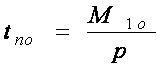 ;
;
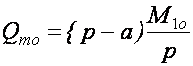 .
.
Или:
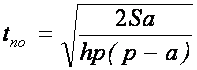 ;
;
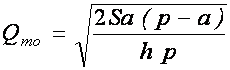 .
.
3. Обобщенная модель определения оптимальных входных параметров
Сравнительный анализ формул, полученных для числа
циклов и исходных объемов финансового и материального потоков технологической
цепи хлебопродуктового объединения, позволяет сделать вывод о том, что они
отличаются лишь коэффициентом (назовем его относительной скоростью поставки и
обозначим через g) в
выражениях для размера партии поставки, равным 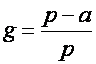 . Исследование этого коэффициента показывает,
что, во-первых, для работоспособной технологической цепи он должен быть больше
нуля (скорость поставки сырья должна быть больше скорости его отгрузки на
переработку), во-вторых, его значение находится в интервале от нуля до единицы
и зависит от скорости поставки сырья: при p = a, g = 0; при p
>> a, g = 1. Очевидно, что если p >> a,
то формулы второй группы, полученные для производственных условий, превращаются
в формулы первой группы (идеальные условия). Таким образом, первая группа
формул представляет собой частный случай второй группы при
. Исследование этого коэффициента показывает,
что, во-первых, для работоспособной технологической цепи он должен быть больше
нуля (скорость поставки сырья должна быть больше скорости его отгрузки на
переработку), во-вторых, его значение находится в интервале от нуля до единицы
и зависит от скорости поставки сырья: при p = a, g = 0; при p
>> a, g = 1. Очевидно, что если p >> a,
то формулы второй группы, полученные для производственных условий, превращаются
в формулы первой группы (идеальные условия). Таким образом, первая группа
формул представляет собой частный случай второй группы при
p >> a.
Используя выражение для коэффициента g, перепишем основные соотношения, представляющие обобщенную модель для расчета параметров технологической цепи хлебопродуктового объединения.
Оптимальный объем исходного материального потока:
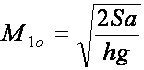 . (18)
. (18)
Оптимальное число циклов:
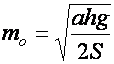 . (19)
. (19)
Минимальный объем исходного финансового потока:
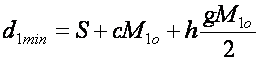 , (20)
, (20)
или
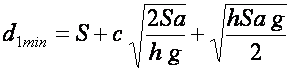 . (21)
. (21)
В хлебопродуктовой
производственной структуре с полным технологическим набором предприятий [1] первые
два звена характеризуются годичным циклом, обусловленным сезонностью
производства в растениеводстве. Поэтому входные потоки ![]() и
и ![]() имеют годовые объемы, а оптимизация материальных
потоков начинается только с потока
имеют годовые объемы, а оптимизация материальных
потоков начинается только с потока ![]() .
.
Полученная обобщенная модель для расчета входных параметров технологической цепи вместе с моделями эффективности, разработанными в [1], составляют математическую основу комплексной количественной методики оценки эффективности и определения входных параметров хлебопродуктового объединения с вертикальной (технологической) интеграцией.
Список литературы
1. Ищенко О.В. Методика и модели оценки эффективности хлебопродуктовых производственных объединений потребительской кооперации / О.В. Ищенко, Т.В. Першакова // Научный журнал КубГАУ [Электронный ресурс]. – Краснодар: КубГАУ, 2005. – №2(10). – Режим доступа: http://ej.kubagro.ru.
2. Крохмаль В.В. Структура 2 производственной системы с вертикальной интеграцией / В.В. Крохмаль, В.И. Лойко // Научный журнал КубГАУ [Электронный ресурс]. – Краснодар: КубГАУ, 2004. – №3(01). – Режим доступа: http://ej.kubagro.ru/2004/01/08/p08.asp.
3. Тернер Д. Вероятность, статистика, исследование операций: Пер. с англ. – М.: Высшая школа, 1971. – 340 с.
Научный электронный журнал КубГАУ . № 02(10), 2005