Научный электронный журнал КубГАУ . № 04(6), 2004
УДК 621.694. 2: 626. 822.4
ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ РОТОРНОЙ КОНСТРУКЦИИ ФРЕЗЫ ТУРБОЭЖЕКТОРНОГО ОКАШИВАЮЩЕГО УСТРОЙСТВА ДЛЯ ГРУНТОВЫХ МЕЛИОРАТИВНЫХ КАНАЛОВ
Аракельян Л.В. – к. т. н., профессор
Бредихин Б.А. – к. т. н., профессор
Суханенко Б.В. – аспирант
Кубанский государственный аграрный университет
В статье приведены математические модели конусной фрезы для окашивающих устройств, применяемых при очистке мелиоративных каналов. Рассмотрены схемы фрезы с различными конструкциями ножей. Даны рекомендации по конструированию конических фрез для различных условий применения.
Экспериментальные исследования процессов очистки мелиоративных каналов, выполненных в земляном русле, от укорененной и плавающей сорной растительности при помощи турбоэжекторного окашивающего устройства (ТЭОУ) выявили некоторые недостатки фрез, используемых для скашивания растительности. Самым существенным из них является то, что применяемая фреза выполняет только часть технологических операций – срезает стебли и корневища растений. Попытки использовать эту фрезу для измельчения растений, которое необходимо с целью эффективного удаления зеленой массы эжектором вместе с водой, оказались недостаточно успешными. В некоторых случаях фреза не измельчала растения, а скручивала их в жгут. Для устранения этого недостатка нами была предложена и исследована в лаборатории так называемая “конусная” фреза.
Экспериментальная фреза представляет собой пространственную конструкцию, по форме близкую к усеченному конусу. Основания ее выполнены в виде колец. Одно из колец, опорное, крепится к ротору ТЭОУ. Между двумя основаниями расположены подвижные ножи, которые при вращении конуса пересекаются с неподвижными ножами, образуя режущую пару.
Для исследования процесса резания конусной фрезы нами была составлена ее математическая модель с целью получения уравнений траектории точки резания и закона ее движения.
На рисунке 1 изображена схема конусной фрезы с прямолинейными ножами
ВС и АВ. ![]()
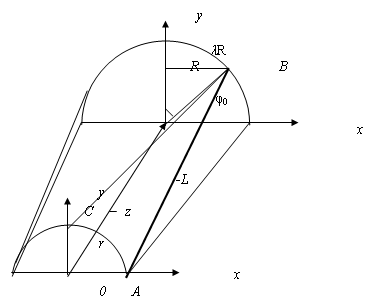
Рисунок 1 – Схема конической фрезы с прямолинейными ножами
Для определенности считаем нож ВС подвижным вместе с внешним конусом,
вращающимся по закону ![]() (
(![]() – относительная угловая скорость
вращения внешнего и внутреннего ножей). Тогда неподвижный нож АВ следует
рассматривать как траекторию точки резания в системе координат, связанной
с неподвижным (внутренним) конусом.
– относительная угловая скорость
вращения внешнего и внутреннего ножей). Тогда неподвижный нож АВ следует
рассматривать как траекторию точки резания в системе координат, связанной
с неподвижным (внутренним) конусом.
Уравнения траектории АВ запишем по координатам концевых точек: А (![]() )
и В (
)
и В (![]() ). В параметрической форме они имеют вид:
). В параметрической форме они имеют вид:
![]() ,
, ![]() ,
, ![]() (1)
(1)
Здесь ![]() – параметр, определяющий положение точки В. Можно показать,
что пересечение ножей по всей длине АВ имеет место только при
– параметр, определяющий положение точки В. Можно показать,
что пересечение ножей по всей длине АВ имеет место только при ![]() , что соответствует
, что соответствует ![]() (см.
рис. 1). В остальных случаях прямолинейные ножи конической фрезы являются
скрещивающимися прямыми.
(см.
рис. 1). В остальных случаях прямолинейные ножи конической фрезы являются
скрещивающимися прямыми.
При ![]() уравнения (1) имеют вид:
уравнения (1) имеют вид:
![]()
![]() ,
, ![]() . (2)
. (2)
Законы движения точек С и В запишем в функции угла поворота φ (рис. 2, 3).
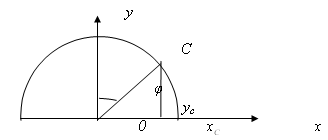
Рисунок 2 – Схема определения координат точки С
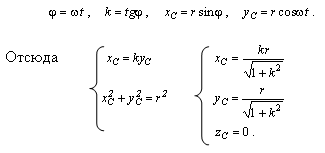

Рисунок 3 – Схема определения координат точки В
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, 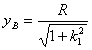 ,
, ![]()
![]()
При ![]() получаем
получаем ![]() ,
, ![]() .
.
При ![]() :
:
![]() ,
, ![]() ,
, ![]()
Здесь ![]() – параметр, определяющий положение подвижного ножа
в процессе вращения фрезы. Его можно рассматривать как условное время.
– параметр, определяющий положение подвижного ножа
в процессе вращения фрезы. Его можно рассматривать как условное время.
Уравнения подвижного ножа ВС запишем по координатам концевых точек С и В. В параметрическом виде они имеют вид:
![]()
 ,
(3)
,
(3)
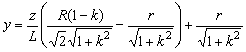 .
.
Решая совместно уравнения прямых АВ и ВС, найдем закон движения точки по траектории АВ в функции параметра k. Приравнивая координаты x в уравнениях АВ и ВС, получим:
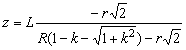 . (4)
. (4)
Аналогично, приравнивая координаты y, получим тот же результат для координаты z. Это подтверждает наличие точки пересечения ножей при любом k. В итоге закон движения точки резания по траектории АВ в функции параметра k в параметрической форме выражается следующим образом:
 ,
,
![]() , (5)
, (5)
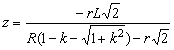 .
.
В частности из (5) следует:
1. При ![]() и
и ![]() :
:
![]() ,
, ![]() –
точка пересечения совпадает с В (начало резания).
–
точка пересечения совпадает с В (начало резания).
2. При ![]()
![]() :
:
![]() ,
,![]() ,
, ![]() – точка пересечения совпадает с А (конец резания).
– точка пересечения совпадает с А (конец резания).
3. При ![]() <k<
<k<![]() – точка пересечения лежит на АВ.
– точка пересечения лежит на АВ.
Наряду с описанной выше рассматривались схемы конической фрезы с криволинейным очертанием неподвижного ножа (рис. 4).
Так, в сечении неподвижного конуса плоскостью
![]()
обнаруживается дуга эллипса (при γ>α) или дуга параболы
(при ![]() ). В этом
случае уравнения траектории точки резания представляют собой систему
уравнений двух поверхностей – секущей плоскости и конуса:
). В этом
случае уравнения траектории точки резания представляют собой систему
уравнений двух поверхностей – секущей плоскости и конуса:
![]() ,
(6)
,
(6)
![]() .
.
В параметрической форме уравнения дуги неподвижного ножа (траектории
точки резания) при ![]() имеют вид:
имеют вид:
![]() ,
, ![]() ,
, 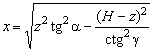 .
(7)
.
(7)
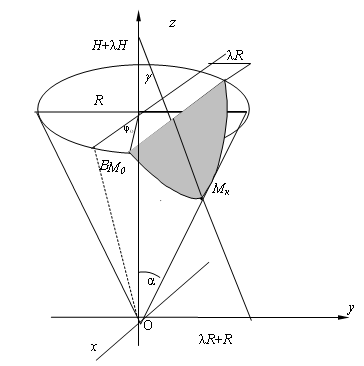
Рисунок 4 – Схема конической фрезы с криволинейным очертанием неподвижного ножа
Уравнения подвижного ножа можно представить в виде системы уравнений
двух поверхностей – конуса и вращающейся плоскости:![]() ,
где
,
где ![]() .
.
Точку резания можно найти как точку пересечения трех поверхностей: секущей плоскости, конуса и вращающейся плоскости:
![]() ,
, ![]() ,
, ![]() . (8)
. (8)
Решение системы (8) дает координаты точки резания в функции параметра ![]() (условное время), т. е. закон движения точки резания
в параметрической форме:
(условное время), т. е. закон движения точки резания
в параметрической форме:
![]() ,
,
![]() ,
(9)
,
(9)
![]() .
.
При ![]() (начало резания)
(начало резания) ![]() и
уравнения (9) дают
и
уравнения (9) дают
![]() ,
, ![]() ,
, ![]() (точка
В).
(точка
В).
При ![]() (конец резания)
(конец резания) ![]() ,
и из уравнений (9) следует:
,
и из уравнений (9) следует:
![]() ,
, ![]() ,
, ![]() (точка М).
(точка М).
При ![]() траекторией точки резания является дуга эллипса
с уравнениями (7).
траекторией точки резания является дуга эллипса
с уравнениями (7).
В случае ![]() , когда секущая плоскость параллельна образующей конуса,
траекторией точки резания является дуга параболы с уравнениями:
, когда секущая плоскость параллельна образующей конуса,
траекторией точки резания является дуга параболы с уравнениями:
![]() ,
, ![]() ,
, ![]() .
(10)
.
(10)
Закон движения точки резания для этого случая принимает вид:
![]() ,
,
![]() ,
(11)
,
(11)
![]() .
.
В случае ![]() , когда секущая плоскость параллельна оси конуса и проходит
на расстоянии
, когда секущая плоскость параллельна оси конуса и проходит
на расстоянии ![]() от нее, в сечении лежит дуга гиперболы
с уравнениями:
от нее, в сечении лежит дуга гиперболы
с уравнениями:
![]() ,
(12)
,
(12)
![]()
или в параметрической форме
![]() ,
, ![]() ,
, ![]() . (13)
. (13)
Закон движения точки резания для гиперболической траектории и прямолинейного подвижного ножа выражается следующим образом:
![]() ,
, ![]() ,
, ![]() (14)
(14)
Началу резания в этом случае соответствует ![]() , окончанию резания –
, окончанию резания – ![]() .
.
Вектор скорости точки резания направлен по касательной к траектории, т. е. по касательной к линии неподвижного ножа. Модуль вектора скорости находится по формуле
![]()
![]() .
.
Здесь точкой обозначено дифференцирование по времени уравнений закона движения точки резания, в которых следует выполнить подстановку
![]() .
.
В результате закон движения (5) принимает вид:
![]() ,
,
![]() , (15)
, (15)
![]() .
.
После дифференцирования по ![]() получаются
следующие уравнения закона изменения скорости резания в течение цикла,
т. е. в интервале
получаются
следующие уравнения закона изменения скорости резания в течение цикла,
т. е. в интервале![]() :
:
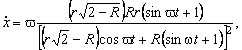

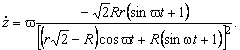
Модуль вектора скорости точки резания выражается формулой
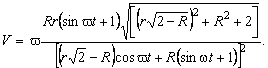 (16)
(16)
Если при ![]() и принятой выше системе координат (см. рис.1) радиусы
оснований усеченного конуса связаны зависимостью
и принятой выше системе координат (см. рис.1) радиусы
оснований усеченного конуса связаны зависимостью
![]() ,
,
то уравнения закона движения (15) существенно упрощаются:
![]()
![]() , (17)
, (17)
![]() .
.
Дифференцированием по ![]() получаются компоненты скорости точки резания:
получаются компоненты скорости точки резания:
![]() ,
,
![]() , (18)
, (18)
![]() .
.
Модуль скорости точки резания выражается формулой
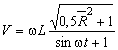 ,
,
или 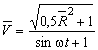 . (19)
. (19)
Здесь ![]() – относительная скорость,
– относительная скорость, ![]() – относительный радиус.
– относительный радиус.
Из формулы (19) следует, что закон изменения относительной скорости
при ![]() и
и ![]() определяется
единственным параметром фрезы
определяется
единственным параметром фрезы ![]() .
.
График ![]() , построенный для значения
, построенный для значения ![]() , можно использовать для фрезы с
, можно использовать для фрезы с ![]() с помощью формулы
с помощью формулы
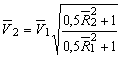 .
.
Угол ![]() между ножами
между ножами ![]() и
и ![]() (см. рис. 1) при произвольном соотношении радиусов
оснований фрезы
(см. рис. 1) при произвольном соотношении радиусов
оснований фрезы ![]() и
и ![]() выражается формулой
выражается формулой
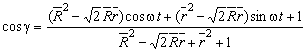 . (20)
. (20)
При соотношении радиусов
![]()
формула существенно упрощается и принимает вид:
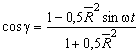 . (21)
. (21)
В итоге при ![]() и принятом соотношении радиусов
и принятом соотношении радиусов ![]() закон изменения угла резания определяется единственным
параметром фрезы
закон изменения угла резания определяется единственным
параметром фрезы ![]() .
.
Каждому значению ![]() соответствует своя кривая закона. Таким образом, семейство
кривых по параметру
соответствует своя кривая закона. Таким образом, семейство
кривых по параметру ![]() охватывает все множество фрез данного
типа.
охватывает все множество фрез данного
типа.
Полученные уравнения и формулы позволяют создать конструкцию и выполнить расчет фрезы, способной не только скашивать растительность, но и измельчать ее. Последнее необходимо для образования гидросмеси и ее последующего удаления из канала гидромеханическим способом.
Научный электронный журнал КубГАУ . № 04(6), 2004