Научный электронный журнал КубГАУ . № 03(5), 2004
УДК 622.011.43
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОДОЛЬНЫХ КОЛЕБАНИЙ И ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ ДЛЯ ЛИНЕЙНО-ВЯЗКОУПРУГОГО СТЕРЖНЯ
Аршинов Г.А. – канд. физ.-мат. наук
Кубанский государственный аграрный университет
Математическая модель продольных колебаний построена на основе вывода и анализа эволюционных уравнений для линейно-вязкоупругого стержня.
Бесконечный стержень, свободный от внешних объемных и поверхностных
воздействий, отнесен к системе координат. Ось x расположена
вдоль оси стержня, а оси y и ![]() – в одном из поперечных сечений.
– в одном из поперечных сечений.
Перемещения точек стержня аппроксимируются с помощью функций
![]() ,
,![]() ,
,![]() ,
(1)
,
(1)
где ![]() – соответственно перемещения по осям x, y, z;
– соответственно перемещения по осям x, y, z; ![]() –
время,
–
время, ![]() –
коэффициент Пуассона.
–
коэффициент Пуассона.
Буквенные индексы переменных функции (1) определяют частную производную от функции по указанной переменной, т. е.
![]() ,
, ![]() и т.д.
и т.д.
Конечные деформации стержня задаются тензором Грина
![]() (2)
(2)
а физико-механические свойства – уравнениями линейной вязкоупругости:
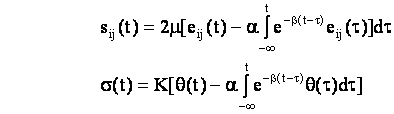 , (3)
, (3)
где ![]() -
соответственно компоненты девиаторов напряжений и деформаций;
-
соответственно компоненты девиаторов напряжений и деформаций; ![]() − среднее напряжение,
− среднее напряжение, ![]() - объемное расширение,
- объемное расширение, ![]() − модуль объемной деформации,
− модуль объемной деформации, ![]() -
параметр Ламе;
-
параметр Ламе; ![]() - константы, определяющие реологические
свойства стержня; Е - модуль Юнга;
- константы, определяющие реологические
свойства стержня; Е - модуль Юнга;![]()
![]() - коэффициент Пуассона.
- коэффициент Пуассона.
При условии ![]() >>1 интегральные операторы в уравнениях
(3) заменяются дифференциальным разложением функции
>>1 интегральные операторы в уравнениях
(3) заменяются дифференциальным разложением функции ![]() в ряд Тейлора по степеням (
в ряд Тейлора по степеням (![]() ) с сохранением двух слагаемых. В результате получаются
приближенные формулы для компонент напряжений
) с сохранением двух слагаемых. В результате получаются
приближенные формулы для компонент напряжений
![]() ,
(4)
,
(4)
где введен оператор L, определяемый равенством ![]() и действующий на функцию
и действующий на функцию ![]() по правилу
по правилу ![]() ,
а
,
а ![]() − параметр Ламе.
− параметр Ламе.
В развернутом виде:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнения движения стержня выводятся из принципа виртуальных работ:
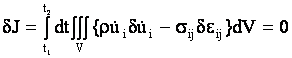 , (5)
, (5)
где точкой обозначена производная по t, r - плотность материала
стержня, ![]() - вариации деформаций,
- вариации деформаций, ![]() – вариации перемещений, а тройной интеграл вычисляется
по объему стержня.
– вариации перемещений, а тройной интеграл вычисляется
по объему стержня.
С учетом (1), (2), (4) определяется вариация внутренней энергии стержня
![]()
![]()
![]()
![]()
+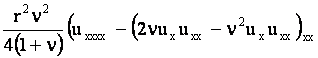
![]() .
.
Уравнение движения стержня получается из (5) после подстановки в него значения вариации внутренней энергии
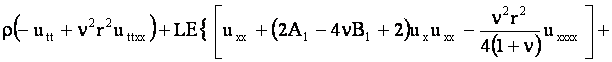

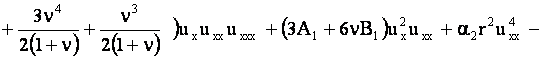
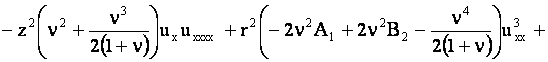
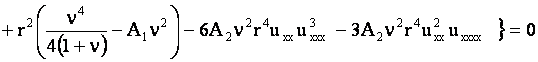
и преобразуется к безразмерным переменным
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
где ![]() –
амплитудный параметр возмущения,
–
амплитудный параметр возмущения, ![]() , d – соответственно характерные длина
волны и поперечный размер стержня,
, d – соответственно характерные длина
волны и поперечный размер стержня, ![]() скорость волны,
скорость волны, 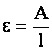 – характеристика нелинейности волнового
процесса.
– характеристика нелинейности волнового
процесса.
Допустим, что 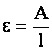 – малый параметр, т.е. характерная длина
волны
– малый параметр, т.е. характерная длина
волны ![]() значительно
превосходит амплитудный параметр
значительно
превосходит амплитудный параметр ![]() ,
а поперечный размер стержня и реологические постоянные
,
а поперечный размер стержня и реологические постоянные ![]() определяют отношения порядков
определяют отношения порядков
![]() ,
, ![]()
![]() .
.
В результате сохранения членами порядка не выше ![]() получается безразмерное уравнение
движения стержня:
получается безразмерное уравнение
движения стержня:

 . (6)
. (6)
Для анализа уравнения (6) применяется метод возмущений. Функция ![]() представляется
в виде асимптотического разложения
представляется
в виде асимптотического разложения
![]() .
(7)
.
(7)
После подстановки (7) в уравнение (6) и с учетом введенных соотношений порядков в нулевом приближении запишем:
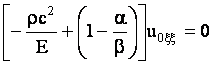 .
.
Согласно условию ![]() , из последнего уравнения определяется скорость распространения
продольной волны в линейно-вязкоупругом стержне:
, из последнего уравнения определяется скорость распространения
продольной волны в линейно-вязкоупругом стержне:
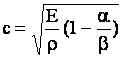 .
(8)
.
(8)
Из формулы (8) при ![]() , т. е. отсутствии свойства вязкости,
вытекает известная формула для скорости распространения продольной
волны в линейно-упругом стержне:
, т. е. отсутствии свойства вязкости,
вытекает известная формула для скорости распространения продольной
волны в линейно-упругом стержне: 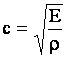 .
.
Для разрешимости уравнения относительно неизвестной
функции ![]() в разложении (7), полученном из
первого приближения, необходимо, чтобы u
в разложении (7), полученном из
первого приближения, необходимо, чтобы u![]() удовлетворяло известному уравнению Кортевега де Вриза
– Бюргерса:
удовлетворяло известному уравнению Кортевега де Вриза
– Бюргерса:
![]() , (9)
, (9)
где
![]() ,
, 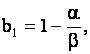
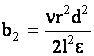 ,
, 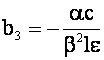 .
.
Точное решение уравнения (9) можно представить:
![]() ,
,
где
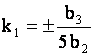 ,
, 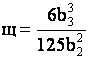 ,
, 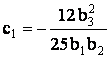 ,
, ![]()
 ,
, ![]() имеет знак
имеет знак ![]() ,
, 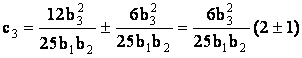 ,
, ![]() .
.
При ![]() запишем неравенства вида
запишем неравенства вида ![]()
![]()
![]() ,
, ![]() .
.
Если в уравнениях выбран верхний знак “+”, то с учетом ![]() и
и ![]() уравнение примет вид:
уравнение примет вид:
![]()
где 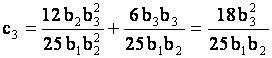 .
.
Из условия ![]() следует, что
следует, что ![]() ,
,
где ![]() , а
, а 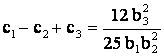 .
.
При ![]()
![]() .
.
Производная ![]()
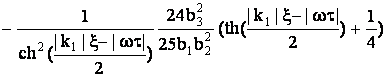 .
.
Критические точки функции определяются уравнением
![]() ,
,
и функция ![]() будет максимальна в точке, определенной значением
будет максимальна в точке, определенной значением ![]() , являющимся корнем уравнения
, являющимся корнем уравнения ![]() .
.
Тогда максимальное значение функции
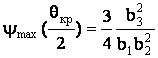 .
.
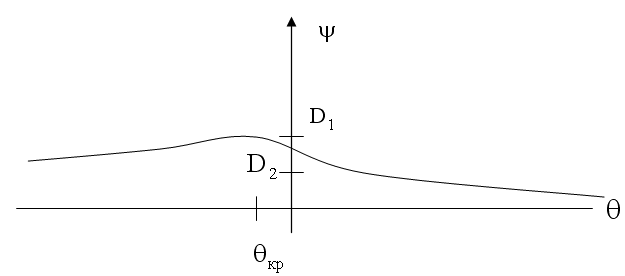
Зависимость деформаций от перемещений
Зависимость деформации от перемещения качественно представлена на рисунке, где введены обoзначения:
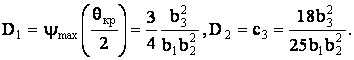
При переходе к размерным переменным вычисляется поправка к скорости
распространения волны, равная ![]() .
.
Научный электронный журнал КубГАУ . № 03(5), 2004