Научный электронный журнал КубГАУ . № 03(5), 2004
УДК 622.011.43
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОДОЛЬНЫХ КОЛЕБАНИЙ ДЛЯ НЕЛИНЕЙНО-ВЯЗКОУПРУГОГО СТЕРЖНЯ
Аршинов Г.А. – к. ф.-м. н.
Кубанский государственный аграрный университет
Исследуются условия возникновения уединенных продольных волн в физически и геометрически нелинейных вязкоупругих стержнях.
В бесконечном стержне, свободном от внешних воздействий, отнесенном
к системе координат с осью x, расположенной вдоль осевой линии
стержня, и осями y, 
– в одном из поперечных сечений, перемещения точек
стержня аппроксимируются функциями
,
,
,
(1)
где 
– соответственно перемещения по осям x, y,
z; 
– время, 
–
коэффициент Пуассона, 
.
Деформации стержня задаются тензором Грина:
(2)
где 
Реологические свойства стержня определяются уравнениями квадратичной теории вязкоупругости [1]:
, (3)
где 
,
– параметры Ламе, 
– объемное расширение, 
– символы Кронекера 
– компоненты девиатора деформаций, 
-реологические константы материала, 
– интенсивность деформаций.
Интегральные операторы в уравнениях (3) заменяются дифференциальными путем разложения функций
в ряд Тейлора по степеням 
.
При условии быстрого затухания памяти материала 
в
разложениях можно сохранить два слагаемых ряда и записать
где введены операторы
, 
,
действующие на функцию 
по правилам
, 
.
Компоненты девиатора деформаций:
,
,
,
,
где 
.
Уравнение движения стержня выводится из вариационного принципа так же, как в работе [2] , и преобразуется к безразмерным переменным
, 
, 
, 
, 
,
где 
–
амплитудный параметр возмущения, 
, d – соответственно характерные длина
волны и поперечный размер стержня, 
скорость волны, 
– характеристика нелинейности волнового
процесса.
Если длина волны l значительно превосходит амплитудный параметр
А, т. е. 
– малый параметр, а поперечные размеры
стержня и реологические постоянные 
определяют
отношения порядков
, 
, 
,
где 
–
характерный размер поперечного сечения,
то безразмерное уравнение движения стержня примет вид:
+
(4)
+
,
где 
, а звездочки отброшены.
Функцию 
представим в виде асимптотического
разложения: 
и подставим в уравнение (4). Из нулевого приближения
следует уравнение:
,
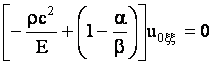где 
– модуль упругости.
Так как 
то скорость распространения волны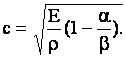 
Из первого приближения вытекает модифицированное уравнение Кортевега де Вриза – Бюргерса:
,
(5)
где 
,
, 
, 
.
Точное решение уравнения (5) находится из сингулярного многообразия
,
(6)
где 
– неизвестные функции независимых переменных.
Подстановка (6) в уравнение (5) дает
,
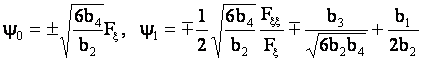где функция 
удовлетворяет уравнению (5).
В результате
. Подстановка в последнее равенство
функции 
приводит к точному решению уравнения (5) в виде:
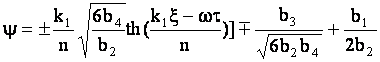, (7)
где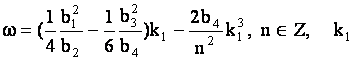 
– произвольный параметр.
Далее исследуются случаи, когда полученное решение описывает структуру ударных волн.
1) Пусть 
и 
,
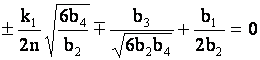тогда 
и
.
В итоге
.
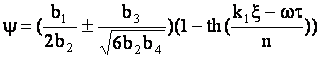Если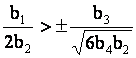 
, то при выбранных условиях в стержне возникает
уединенная ударная волна растяжения 
, если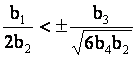 
– волна сжатия 
.
2) Пусть 
и 
,
тогда
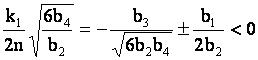
и
.
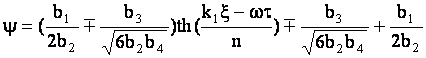В результате
.
Если 
или 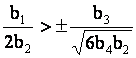, то при указанных условиях в оболочке
возникает ударная волна растяжения 
.
Если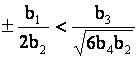 
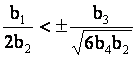или , то при выбранных условиях – ударная волна
сжатия 
.
Из проведенного исследования следует: как при 
, так и 
в случае выполнения условия 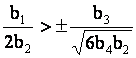в физически и геометрически нелинейном
вязкоупругом стержне возникает уединенная ударная волна растяжения.
Если выполняется условие ,
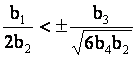то образуется ударная волна сжатия.
Как и в линейном случае [2], при переходе к размерным переменным
получается поправка к скорости распространения волны 
.
Список литературы
1. Москвитин В.В. Сопротивление вязкоупругих материалов. М.: Наука, 1972.
2. Аршинов Г.А. Математическая модель продольных колебаний и эволюционные уравнения для линейно-вязкоупругого стержня // Научный журнал КубГАУ. 2004. № 3 (5). http: //ej.kubagro.ru.
Научный электронный журнал КубГАУ . № 03(5), 2004