Научный электронный журнал КубГАУ . № 02(4), 2004
ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АКУСТОМАГНИТНОЙ ОБРАБОТКИ ЖИДКОГО ТОПЛИВА
Коржаков Алексей Валерьевич - соискатель, ст. преподаватель
Адыгейский государственный университет
Лойко Валерий Иванович - д.т.н., профессор
Кубанский государственный аграрный университет
Результаты исследований обработки жидкого топлива показали, что применение одновременной обработки магнитным и акустическим полем дают возможность увеличить степень сгорания топлива, и как следствие уменьшить расход топлива. Построенная модель позволяет выбрать оптимальные параметры АМА для конкретного типа автотранспорта.
Актуальность темы исследования. На современном этапе развития техники происходит быстрая смена моделей выпускаемой продукции, появляются разработки, выполненные на новых принципах, обеспечивающих изделиям более высокие потребительские качества. Это приводит к необходимости улучшения процессов создания новой техники, повышению качества проектов, разработки и организации производства. При этом должно происходить снижение затрат как финансовых, так и трудовых, увеличиваться прибыль.
В данной работе предлагается использовать новые методы очистки отработанных газов от вредных примесей. Для решения этой задачи необходимо обеспечить более полное сгорание топлива двигателей автотранспорта. Для этого предлагается провести предварительную обработку топлива автомобильных двигателей в акустических и электромагнитных полях.
Этот метод можно реализовать при помощи акусто-магнитного аппарата (АМА) который устанавливается в систему питания двигателей внутреннего сгорания с целью повышения эффективности сгорания топлива. Более полное сгорание топлива приводит к снижению содержания вредных примесей в отработанных газах, что в свою очередь способствует улучшению экологической обстановки (косвенный показатель полноты сгораемости топлива - расход топлива на сто километров).
Предварительные исследования экологической эффективности данного метода в лабораторных и реальных условиях показали, что в отработанных газах резко снижается содержание тяжелых металлов и углерода. В результате проведения прямых многократных измерений были получены и обработаны измеряемые величины: расход топлива за единицу пройденного пути.
Измерение расхода топлива проходило в абсолютно одинаковых условиях: на одном и том же отрезке дороги, в одном направлении движения, в одно время суток. Сначала проводилась серия опытов на автомобилях с карбюраторными и инжекторными двигателями отечественного производства без АМА. Исследования носили оптимизационный характер и были нацелены на достижение высоких показателей технического уровня и эффективности создаваемого изделия (АМА). Для решения задач такого типа используются методы математического моделирования и планирования эксперимента.
Применение методов планирования экспериментов может дать экономический эффект более или менее значительный, но их отсутствие может сделать экспериментальную программу полностью безрезультатной.
Математические методы планирования эксперимента во многих случаях общие для моделей имеющих различное происхождение.
Целью исследования является оптимизация технических показателей эффективности создаваемого изделия (АМА), разработка и анализ математической модели на основе методов планирования эксперимента и обработки информации.
В таблице 1 приведены результаты измерения расхода топлива на сто километров для автомобилей отечественного производства с карбюраторным двигателем до установки АМА.
| №изм | Доза топлива(литр) | Частота вращения двигателя | Пройденный путь (км) |
Расход топлива на 100 км/час (xi) |
| 1 | 1 литр | 2500 | 12,89 | 7,76 |
| 2 | 1 литр | 2500 | 13,11 | 7,63 |
| 3 | 1 литр | 2500 | 13,22 | 7,56 |
| 4 | 1 литр | 2500 | 13,27 | 7,54 |
| 5 | 1 литр | 2500 | 13,31 | 7,51 |
| 6 | 1 литр | 2500 | 13,36 | 7,49 |
| 7 | 1 литр | 2500 | 13,44 | 7,44 |
| 8 | 1 литр | 2500 | 13,56 | 7,38 |
| 9 | 1 литр | 2500 | 13,60 | 7,35 |
| 10 | 1 литр | 2500 | 13,11 | 7,63 |
| 11 | 1 литр | 2500 | 13,00 | 7,69 |
| 12 | 1 литр | 2500 | 12,96 | 7,72 |
| 13 | 1 литр | 2500 | 12,67 | 7,89 |
| 14 | 1 литр | 2500 | 13,33 | 7,50 |
| 15 | 1 литр | 2500 | 13,38 | 7,48 |
| 16 | 1 литр | 2500 | 13,27 | 7,54 |
| 17 | 1 литр | 2500 | 12,89 | 7,76 |
| 18 | 1 литр | 2500 | 12,96 | 7,72 |
| 19 | 1 литр | 2500 | 12,93 | 7,73 |
| 20 | 1 литр | 2500 | 13,11 | 7,63 |
| 21 | 1 литр | 2500 | 13,24 | 7,55 |
| 22 | 1 литр | 2500 | 13,29 | 7,53 |
| 23 | 1 литр | 2500 | 13,18 | 7,59 |
| 24 | 1 литр | 2500 | 13,33 | 7,50 |
| 25 | 1 литр | 2500 | 13,00 | 7,69 |
| 26 | 1 литр | 2500 | 12,89 | 7,76 |
| 27 | 1 литр | 2500 | 12,87 | 7,77 |
| 28 | 1 литр | 2500 | 13,20 | 7,58 |
| 29 | 1 литр | 2500 | 13,18 | 7,59 |
| 30 | 1 литр | 2500 | 12,84 | 7,79 |
Для нахождения наиболее близкого к истинному значение измеряемой величины найдем среднее арифметическое ряда отдельных измерений (выборочное среднее), являющееся несмещенной оценкой математического ожидания (МО) случайной величины.
![]() =7,61 . (1)
=7,61 . (1)
Результаты отдельных измерений отличаются от среднего значения. Эти отклонения носят названия абсолютных погрешностей. Проведем формирование групп результатов.
| № группы | xi | Ni | |
|
|
| 1 | 7,38 | 2 | -0,23 | 0,0529 | 0,1058 |
| 2 | 7,44 | 1 | -0,17 | 0,0289 | 0,0289 |
| 3 | 7,48 | 2 | -0,13 | 0,0169 | 0,0338 |
| 4 | 7,51 | 3 | -0,10 | 0,0100 | 0,03 |
| 5 | 7,54 | 3 | -0,07 | 0,0049 | 0,0147 |
| 6 | 7,55 | 2 | -0,06 | 0,0036 | 0,0072 |
| 7 | 7,59 | 3 | -0,02 | 0,0004 | 0,0012 |
| 8 | 7,63 | 6 | 0,02 | 0,0004 | 0,0024 |
| 9 | 7,69 | 2 | 0,08 | 0,0064 | 0,0128 |
| 10 | 7,72 | 3 | 0,11 | 0,0121 | 0,0363 |
| 11 | 7,76 | 2 | 0,15 | 0,0225 | 0,045 |
| 12 | 7,89 | 1 | 0,28 | 0,0784 | 0,0784 |
Абсолютные ошибки отдельных измерений некоторой величины в какой-то степени характеризуют точность каждого из измерений или разброс измеряемых значений. Перейдем к выборке отклонений от среднего арифметического значения (таблица 2).
В качестве количественной меры разброса выбрано математическое ожидание квадрата случайных отклонений наблюдений - дисперсия.
Точечная оценка дисперсии, определяется по формуле:
![]() . (2)
. (2)
Среднеквадратическое отклонение (СКО) случайной величины X определяется как корень квадратный из дисперсии. Соответственно его оценка может быть найдена путем извлечения корня из оценки дисперсии. Однако эта операция является нелинейной процедурой, приводящей к смещенности получаемой таким образом оценки. Для исправления оценки СКО введем поправочный множитель k(n), зависящий от числа наблюдений n. Он изменяется от k(3) = 1,13 до k(∞) ≈ 1,03. Оценка среднего квадратического отклонения
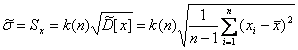 . (3)
. (3)
Полученные оценки МО и СКО являются случайными величинами. Это проявляется в том, что при повторениях серий из n наблюдений каждый раз будут получаться различные оценки ![]() и
и ![]() , Рассеяние этих оценок целесообразно оценивать с помощью СКО
, Рассеяние этих оценок целесообразно оценивать с помощью СКО ![]() и
и ![]() . Оценка СКО среднего арифметического значения
. Оценка СКО среднего арифметического значения
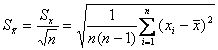 . (4)
. (4)
Оценка СКО среднего квадратического отклонения
![]() (5)
(5)
Отсюда следует, что относительная погрешность определения СКО может быть оценена как
![]() (6)
(6)
Она зависит только от эксцесса и числа наблюдений в выборке и не зависит от СКО, т.е. той точности, с которой производятся измерения. Ввиду того, что большое число измерений проводится относительно редко, погрешность определения σ может быть весьма существенной. В любом случае она больше погрешности из-за смещенности оценки, обусловленной извлечением квадратного корня и устраняемой поправочным множителем k(n). В связи с этим пренебрегаем учетом смещенности оценки СКО отдельных наблюдений и определяем его по формуле
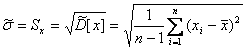 = 0.126 , (7)
= 0.126 , (7)
т.е. считают k(n)=1.
Для того чтобы определить точечные оценки закона распределения необходимо исключить грубые погрешности или промахи в результатах измерений.
Используем Критерий Шарлье, число наблюдений в ряду велико (n > 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину КшSx, будет ![]() , где Ф(Кш) - значение нормированной функции Лапласа для Х=Кш.
, где Ф(Кш) - значение нормированной функции Лапласа для Х=Кш.
Если сомнительным в ряду результатов наблюдений является один результат, то n[1-Ф(Кш)]=1. Отсюда Ф(Кш)=(n-1)/n. Значения критерия Шарлье приведены в таблице 3.
| n | 5 | 10 | 20 | 30 | 40 | 50 | 100 |
| Кш | 1,3 | 1,65 | 1,96 | 2,13 | 2,24 | 2,32 | 2,58 |
Пользуясь критерием Шарлье, отбрасываем результат, для значения которого в ряду из n наблюдений выполняется неравенство ![]()
Если, ![]() =0.269 ,то необходимо отбросить результат 7,89.
=0.269 ,то необходимо отбросить результат 7,89.
После исключения грубой погрешности перейдем к формированию нового ряда и групп результатов. Запишем полученные данные в таблицу 4.
Найдем среднее арифметическое значение ряда отдельных измерений (8).
![]() =7,60.
=7,60.
Рассчитаем среднее квадратическое отклонение (3):
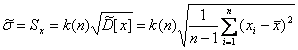 =0,105.
=0,105.
| № группы | xi | Ni | |
|
|
| 1 | 7,38 | 2 | -0,22 | 0,049 | 0,097 |
| 2 | 7,44 | 1 | -0,16 | 0,026 | 0,026 |
| 3 | 7,48 | 2 | -0,12 | 0,014 | 0,029 |
| 4 | 7,51 | 3 | -0,09 | 0,008 | 0,024 |
| 5 | 7,54 | 3 | -0,06 | 0,004 | 0,011 |
| 6 | 7,55 | 2 | -0,05 | 0,003 | 0,005 |
| 7 | 7,59 | 3 | -0,01 | 0,000 | 0,000 |
| 8 | 7,63 | 6 | 0,03 | 0,001 | 0,005 |
| 9 | 7,69 | 2 | 0,09 | 0,008 | 0,016 |
| 10 | 7,72 | 3 | 0,12 | 0,014 | 0,043 |
| 11 | 7,76 | 2 | 0,16 | 0,025 | 0,051 |
Определим закон распределения результатов измерения.
Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному закону распределения возможно с использованием специального критерия ![]() - Пирсона. Критерием Пирсона является случайная величина, распределённая по закону
- Пирсона. Критерием Пирсона является случайная величина, распределённая по закону ![]() (“хи-квадрат”)
(“хи-квадрат”)
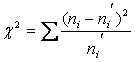 . (8)
. (8)
Эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частотам. Вычислим выборочную среднюю и выборочное среднее квадратическое отклонение методом произведений. Для этого перейдем от заданного интервального распределения к распределению равноотстоящих вариантов, приняв в качестве варианты ![]() среднее арифметическое концов интервала:
среднее арифметическое концов интервала: ![]() . В итоге получим распределение представленное в таблице 5.
. В итоге получим распределение представленное в таблице 5.
Выполнив выкладки по методу произведений, найдем выборочную среднюю и выборочное среднее квадратическое отклонение: ![]() ,
, ![]() =0,099.
=0,099.
Определим шаг по формуле Стерджеса:
к = 1+3,32 lg n=1+3,32lg29=4.8,
![]() =0.076. (9)
=0.076. (9)
Найдем интервалы ![]() , учитывая, что
, учитывая, что ![]() ,
, ![]() =0,099,
=0,099, ![]() =10,05.
=10,05.
Для этого составим расчетную таблицу 5 (левый конец первого интервала примем равным ![]() , а правый конец последнего интервала
, а правый конец последнего интервала ![]() ).
).
| Номер интервала i | Граница интервалов | |
|
|
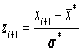 Границы интервалов |
|||||||||
| 1 | 7,38 | 7,46 | 3 | 7,420 | -0,22 | -0,14 | - | -1,400 | ||||||
| 2 | 7,46 | 7,54 | 5 | 7,5 | -0,14 | -0,06 | -1,400 | -0,596 | ||||||
| 3 | 7,54 | 7,62 | 8 | 7,580 | -0,06 | 0,02 | -0,596 | 0,208 | ||||||
| 4 | 7,62 | 7,70 | 8 | 7,66 | 0,02 | 0,10 | 0,208 | 1,012 | ||||||
| 5 | 7,7 | 7,78 | 5 | 7,740 | 0,10 | 0,18 | 1,012 | - | ||||||
| Сумма | 29 | 7,60 | -0,30 | 0,10 | ||||||||||
Найдем теоретические вероятности ![]() и теоретические частоты
и теоретические частоты ![]() Для этого составим расчетную таблицу 6.
Для этого составим расчетную таблицу 6.
| Номер интервала i |
Граница интервалов | |||||
| |
||||||
| 1 | - | -1,40 | -0,500 | -0,4192 | 0,0808 | 2,3432 |
| 2 | -1,40 | -0,60 | -0,4192 | -0,2257 | 0,1935 | 5,6115 |
| 3 | -0,60 | 0,21 | -0,2257 | 0,0832 | 0,3089 | 8,9581 |
| 4 | 0,21 | 1,01 | 0,0832 | 0,3438 | 0,2606 | 7,5574 |
| 5 | 1,01 | - | 0,3438 | 0,5000 | 0,1562 | 4,5298 |
| Сумма | 1,000 | 29 | ||||
Сравним эмпирические и теоретические частоты, используя критерий Пирсона:
1) Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу 7. Столбцы 7 и 8 служат для контроля вычислений по формуле
![]() . (10)
. (10)
Контроль: ![]() =29,43-29=0,43=
=29,43-29=0,43=![]() . Вычисления произведены правильно;
. Вычисления произведены правильно;
2) По таблице критических точек распределения ![]() , по уровню значимости
, по уровню значимости ![]() и числу степеней свободы
и числу степеней свободы ![]() находим критическую точку правосторонней критической области
находим критическую точку правосторонней критической области ![]() =6.
=6.
| |
|||||||
| 1 | 3 | 2,34 | 0,657 | 0,43139 | 0,18 | 9 | 3,84 |
| 2 | 5 | 5,61 | -0,612 | 0,37393 | 0,07 | 25 | 4,46 |
| 3 | 8 | 8,96 | -0,958 | 0,91796 | 0,10 | 64 | 7,14 |
| 4 | 8 | 7,56 | 0,443 | 0,19589 | 0,03 | 64 | 8,47 |
| 5 | 5 | 4,5298 | 0,470 | 0,22109 | 0,05 | 25 | 5,52 |
| сумма | 29 | 29,00 | 0,43 | 187 | 0,43 |
Так как ![]() <
<![]() - принимаем гипотезу о нормальном законе распределения генеральной совокупности. Расхождение между эмпирическими частотами и теоретическими частотами незначимо.
- принимаем гипотезу о нормальном законе распределения генеральной совокупности. Расхождение между эмпирическими частотами и теоретическими частотами незначимо.
Проверка закона по критерию Пирсона показывает, что распределение величин подчиняется нормальному закону Гаусса. Зная закон распределения можно перейти к нахождению квантильного множителя ![]() при заданном значении доверительной вероятности P=0.95. Доверительные границы случайной погрешности можно записать как
при заданном значении доверительной вероятности P=0.95. Доверительные границы случайной погрешности можно записать как ![]()
![]() .
.
Находим среднее квадратическое отклонение от среднего значения (4):
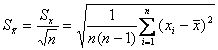 =0,0194.
=0,0194.
Так как гипотеза о нормальности распределения не противоречит опытным данным, доверительный интервал определяется по формуле [3]:
![]() . (11)
. (11)
Отсюда ![]() =0,475. Из таблицы значений функции Лапласа, находим, что
=0,475. Из таблицы значений функции Лапласа, находим, что ![]() =1,96.
=1,96.
Подставляем полученные значения в формулу ![]() =
=![]() .
.
Перейдем к вычислению границы суммарной неисключенной систематической погрешности результата измерения. Неисключенная систематическая погрешность результата образуется из неисключенных погрешностей метода, средства измерения, погрешностей поправок. При суммировании эти составляющие рассматриваются как случайные величины. Данные о виде несключенных составляющих систематических погрешностей отсутствуют, поэтому их распределение принимаем за равномерное. При равномерном распределении неисключенных систематических погрешностей границы неисключенной систематической погрешности результата измерения ![]() вычисляют по формуле:
вычисляют по формуле:
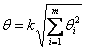 , (12)
, (12)
где ![]() - граница
- граница ![]() -й неисключенной составляющей систематической погрешности;
-й неисключенной составляющей систематической погрешности;
k – коэффициент, определяемый заданной доверительной вероятностью (при
![]()
![]() ;
;
![]() - количество неисключенных составляющих.
- количество неисключенных составляющих.
Определим границы неисключенной составляющей метода измерения. Для нахождения ошибки метода измерения нужно, использовать формулу для вычисления исходной величины
![]() ,
,
где V – расход топлива на сто километров;
G – доза топлива потраченного на прохождения пути до полной остановки двигателя автомобиля;
S – расстояние пройденное автомобилем от момента начала измерения до полной остановки.
Необходимо найти формулу для абсолютной или для относительной ошибки измеряемой величины[1]. Абсолютная ошибка:
![]() =
=![]() .
.
Относительная ошибка:
![]() .
.
Подставим в полученные формулы вместо ошибок измерений точность приборов (класс точности – 0,5), которые использовались для измерения, а вместо значений, непосредственно измеренных на опыте величин – их приближенные значения получим ошибку метода измерения ![]() .
.
Определим погрешности при проведении измерений, учитывая, что автомобиль останавливается не сразу после остановки двигателя. Относительная ошибка – ![]() 0,014
0,014
Абсолютная ошибка – 0,195.
Найдем границы неисключенной систематической погрешности результата измерения ![]() по формуле (12):
по формуле (12):
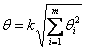 =
=![]() .
.
Границы неисключенной составляющей систематической погрешности и оценки СКО результата измерений S связаны соотношением
0.0152<![]() <0.152.
<0.152.
При невыполнении неравенств ![]() <0.8S; и
<0.8S; и ![]() >8S границу суммарной погрешности ГОСТ 8.207-76 предписывает находить путем композиции распределений случайных и неисключенных систематических погрешностей, рассматривая как случайные величины. Допускается границы погрешности результата измерений определять по формуле:
>8S границу суммарной погрешности ГОСТ 8.207-76 предписывает находить путем композиции распределений случайных и неисключенных систематических погрешностей, рассматривая как случайные величины. Допускается границы погрешности результата измерений определять по формуле:
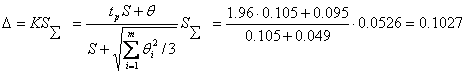 , (13)
, (13)
где 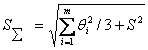 - оценка суммарного СКО суммарной погрешности.
- оценка суммарного СКО суммарной погрешности.
Однако данный подход приводит к заниженным оценкам. Согласно рекомендациям Сергеева А.Г. [3], возможно, рассмотреть этот вопрос в другой плоскости. Если систематическая составляющая постоянна, то ее модуль должен суммироваться с доверительным интервалом случайной составляющей ![]() . Доверительный интервал суммарной погрешности
. Доверительный интервал суммарной погрешности ![]() =2(0,095+0,038)=0,266.
=2(0,095+0,038)=0,266.
Результат измерений записывается в виде V= 7.6![]() при доверительной вероятности
при доверительной вероятности ![]() . Полученный результат соответствует контрольным замерам, данным в технической документации на данный вид автотранспорта.
. Полученный результат соответствует контрольным замерам, данным в технической документации на данный вид автотранспорта.
Ряд измеренных значений расхода топлива на сто километров для автомобилей отечественного производства с инжекторной системой питания двигателя приведен в таблице 8
| №изм | Дозатоплива(Литр) | Частота вращения двигателя |
Пройденный путь (км) |
Расход топлива на 100 км/час (xi) |
| 1 | 1 литр | 2500 | 14,90 | 6,71 |
| 2 | 1 литр | 2500 | 14,78 | 6,77 |
| 3 | 1 литр | 2500 | 15,03 | 6,65 |
| 4 | 1 литр | 2500 | 14,85 | 6,74 |
| 5 | 1 литр | 2500 | 14,78 | 6,77 |
| 6 | 1 литр | 2500 | 14,71 | 6,80 |
| 7 | 1 литр | 2500 | 14,68 | 6,81 |
| 8 | 1 литр | 2500 | 14,91 | 6,71 |
| 9 | 1 литр | 2500 | 14,69 | 6,81 |
| 10 | 1 литр | 2500 | 14,95 | 6,69 |
| 11 | 1 литр | 2500 | 14,98 | 6,67 |
| 12 | 1 литр | 2500 | 14,89 | 6,71 |
| 13 | 1 литр | 2500 | 15,02 | 6,66 |
| 14 | 1 литр | 2500 | 15,08 | 6,63 |
| 15 | 1 литр | 2500 | 14,95 | 6,69 |
| 16 | 1 литр | 2500 | 14,77 | 6,77 |
| 17 | 1 литр | 2500 | 14,71 | 6,80 |
| 18 | 1 литр | 2500 | 14,92 | 6,70 |
| 19 | 1 литр | 2500 | 15,03 | 6,65 |
| 20 | 1 литр | 2500 | 14,83 | 6,74 |
| 21 | 1 литр | 2500 | 14,82 | 6,75 |
| 22 | 1 литр | 2500 | 14,95 | 6,69 |
| 23 | 1 литр | 2500 | 15,06 | 6,64 |
| 24 | 1 литр | 2500 | 14,68 | 6,81 |
| 25 | 1 литр | 2500 | 15,04 | 6,65 |
| 26 | 1 литр | 2500 | 14,85 | 6,73 |
| 27 | 1 литр | 2500 | 14,79 | 6,76 |
| 28 | 1 литр | 2500 | 14,81 | 6,75 |
| 29 | 1 литр | 2500 | 14,78 | 6,76 |
| 30 | 1 литр | 2500 | 15,04 | 6,65 |
Для нахождения наиболее близкого к истинному значению измеряемой величины, найдем среднее арифметическое значение ряда отдельных измерений (1).
![]() 6,72
6,72
Проведем формирование групп результатов.
| № группы | xi | Ni |
| 1 | 6,64 | 2 |
| 2 | 6,66 | 1 |
| 3 | 6,67 | 4 |
| 4 | 6,68 | 1 |
| 5 | 6,69 | 3 |
| 6 | 6,71 | 3 |
| 7 | 6,72 | 3 |
| 8 | 6,73 | 2 |
| 9 | 6,74 | 1 |
| 10 | 6,75 | 3 |
| 11 | 6,76 | 4 |
| 12 | 6,81 | 3 |
Рассчитаем среднее квадратическое отклонения (3):
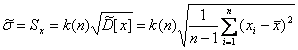 =0,108.
=0,108.
| №группы | xi | Ni | |||
| 1 | 6,64 | 2 | -0,17 | 0,0289 | 0,0578 |
| 2 | 6,66 | 1 | -0,15 | 0,0225 | 0,0225 |
| 3 | 6,67 | 4 | -0,14 | 0,0196 | 0,0784 |
| 4 | 6,68 | 1 | -0,13 | 0,0169 | 0,0169 |
| 5 | 6,69 | 3 | -0,12 | 0,0144 | 0,0432 |
| 6 | 6,71 | 3 | -0,10 | 0,0100 | 0,03 |
| 7 | 6,72 | 3 | -0,09 | 0,0081 | 0,0243 |
| 8 | 6,73 | 2 | -0,08 | 0,0064 | 0,0128 |
| 9 | 6,74 | 1 | -0,07 | 0,0049 | 0,0049 |
| 10 | 6,75 | 3 | -0,06 | 0,0036 | 0,0108 |
| 11 | 6,76 | 4 | -0,05 | 0,0025 | 0,01 |
| 12 | 6,81 | 3 | 0,09 | 0,0082 | 0,024661333 |
Для того чтобы определить точечные оценки закона распределения необходимо исключить грубые погрешности или промахи в результатах измерений. Пользуясь критерием Шарлье, отбрасываем результат, для значения которого в ряду из n наблюдений выполняется неравенство ![]() Если,
Если, ![]() =0.229, то все результаты входят в заданные границы.
=0.229, то все результаты входят в заданные границы.
Приступим к определению закона распределения результатов измерения.
Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному закону распределения возможно с использованием специального критерия ![]() - Пирсона.
- Пирсона.
Вычислим выборочную среднюю и выборочное среднее квадратическое отклонение методом произведений. В итоге получим распределение представленное в таблице 10.
Определим шаг по формуле Стерджеса (9):
![]() =
=![]() .
.
Найдем интервалы ![]() , учитывая, что
, учитывая, что ![]() ,
, ![]() =0,035,
=0,035, ![]() =28,66.
=28,66.
Для этого составим расчетную таблицу 10 (левый конец первого интервала примем равным ![]() , а правый конец последнего интервала
, а правый конец последнего интервала ![]() ).
).
Найдем теоретические вероятности ![]() и теоретические частоты
и теоретические частоты ![]() Для этого составим расчетную таблицу 11.
Для этого составим расчетную таблицу 11.
| Номер интервала i | Граница интервалов | |
|
|
|
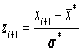 Границы интервалов Границы интервалов |
||||||||||||
| 1 | 6,64 | 6,669 | 3 | 6,655 | -0,08 | -0,05 | - | -1,481 | ||||||||||
| 2 | 6,669 | 6,698 | 8 | 6,684 | -0,05 | -0,02 | -1,481 | -0,650 | ||||||||||
| 3 | 6,698 | 6,726 | 6 | 6,712 | -0,02 | 0,01 | -0,650 | 0,153 | ||||||||||
| 4 | 6,726 | 6,755 | 6 | 6,741 | 0,01 | 0,03 | 0,153 | 0,984 | ||||||||||
| 5 | 6,755 | 6,784 | 4 | 6,770 | 0,03 | 0,06 | 0,984 | 1,815 | ||||||||||
| 6 | 6,784 | 6,813 | 3 | 6,799 | 0,06 | 0,09 | 1,815 | - | ||||||||||
| Сумма | 30 | 6,72 | -0,05 | 0,12 | ||||||||||||||
Таблица 12.
| Номер интервала i | Граница интервалов | ||||||
| |
|||||||
| 1 | - | -1,48 | -0,500 | -0,4306 | 0,0694 | 2,082 | |
| 2 | -1,48 | -0,65 | -0,4306 | -0,2422 | 0,1884 | 5,652 | |
| 3 | -0,65 | 0,15 | -0,2422 | 0,0596 | 0,3018 | 9,054 | |
| 4 | 0,15 | 0,98 | 0,0596 | 0,3365 | 0,2769 | 8,307 | |
| 5 | 0,98 | 1,81 | 0,3365 | 0,4649 | 0,1284 | 3,852 | |
| 6 | 1,81 | - | 0,4649 | 0,5000 | 0,0351 | 1,053 | |
| Сумма | 1,000 | 30 | |||||
Сравним эмпирические и теоретические частоты, используя критерий Пирсона:
1) Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу 12.
2) По таблице критических точек распределения ![]() , по уровню значимости
, по уровню значимости ![]() и числу степеней свободы
и числу степеней свободы ![]() находим критическую точку правосторонней критической области
находим критическую точку правосторонней критической области ![]() =7,8.
=7,8.
| |
|||||||
| 1 | 3 | 2,08 | 0,918 | 0,84272 | 0,40 | 9 | 4,32 |
| 2 | 8 | 5,65 | 2,348 | 5,5131 | 0,98 | 64 | 11,32 |
| 3 | 6 | 9,05 | -3,054 | 9,32692 | 1,03 | 36 | 3,98 |
| 4 | 6 | 8,31 | -2,307 | 5,32225 | 0,64 | 36 | 4,33 |
| 5 | 4 | 3,85 | 0,148 | 0,0219 | 0,01 | 16 | 4,15 |
| 6 | 3 | 1,053 | 1,947 | 3,79081 | 3,60 | 9 | 8,55 |
| сумма | 30 | 30,00 | 6,657 | 170 | 6,657 |
Так как ![]() <
<![]() - принимаем гипотезу о нормальном законе распределения генеральной совокупности. Расхождение между эмпирическими частотами и теоретическими частотами незначимо.
- принимаем гипотезу о нормальном законе распределения генеральной совокупности. Расхождение между эмпирическими частотами и теоретическими частотами незначимо.
Проверка по критерию Пирсона показывает, что распределение величин подчиняется нормальному закону Гаусса. Зная закон распределения можно перейти к нахождению квантильного множителя ![]() при заданном значении доверительной вероятности P=0.95. Доверительные границы случайной погрешности можно записать как
при заданном значении доверительной вероятности P=0.95. Доверительные границы случайной погрешности можно записать как ![]()
![]() .
.
Находим среднее квадратическое отклонение от среднего значения (4):
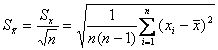 =0,108/5,477=0,02.
=0,108/5,477=0,02.
Так как гипотеза о нормальности распределения не противоречит опытным данным, доверительный интервал определяется по формуле (11): ![]() .
.
Отсюда ![]() =0,475. Из таблицы значений функции Лапласа, находим, что
=0,475. Из таблицы значений функции Лапласа, находим, что ![]() =1,96.
=1,96.
Подставляем полученные значения в формулу ![]() =
=![]() .
.
Доверительный интервал суммарной погрешности
![]() =2(0,095+0,039)=0,268.
=2(0,095+0,039)=0,268.
Результат измерений записывается в виде V=6,72![]() при доверительной вероятности
при доверительной вероятности ![]() .
.
Следующая серия опытов была проведена после установки на автомобиль АМА.
На основе проведенных экспериментов непосредственно на самом техническом объекте (автомобиле) была построена экспериментальная факторная модель, так как сложность системы и условия функционирования не позволяют надеяться на требуемую точность их математического описания теоретическими методами.
Для получения адекватной математической модели необходимо обеспечить выполнение определенных условий проведения эксперимента. При проведении активного эксперимента задается определенный план варьирования факторов, т. е. эксперимент заранее планируется.
В активном эксперименте факторы могут принимать только фиксированные значения. Минимальный Х min и максимальный – Х max, уровни всех факторов выделяем в факторное пространство, некоторый гиперпараллелепипед, представляющий собой область планирования. В области планирования находятся все возможные значения факторов, используемые в эксперименте [2].
Вектор ![]() задает точку центра области планирования. Координаты этой точки
задает точку центра области планирования. Координаты этой точки ![]() выбираем из соотношения:
выбираем из соотношения:
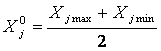 .
.
Точку ![]() определяет основной уровень факторов
определяет основной уровень факторов ![]() . Интервал варьирования фактора Xj, вычисляем по формуле
. Интервал варьирования фактора Xj, вычисляем по формуле
DXj = (Xj max – Xj min).
Факторы нормируем, а их уровни кодируем. В кодированном виде верхний уровень обозначают +1, нижний -1, а основной 0. Нормирование факторов осуществляют на основе соотношения
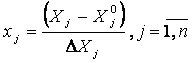 .
.
Для переменных ![]() начало координат совмещено с центром эксперимента, а в качестве единиц измерения используем интервалы варьирования факторов. Центр эксперимента находится в точке 0 с координатами
начало координат совмещено с центром эксперимента, а в качестве единиц измерения используем интервалы варьирования факторов. Центр эксперимента находится в точке 0 с координатами ![]() . Точки 1,2,3,4 являются точками плана эксперимента. План эксперимента удобно представлять в матричной форме.
. Точки 1,2,3,4 являются точками плана эксперимента. План эксперимента удобно представлять в матричной форме.
Матрица спектра плана имеет вид:
 . (14)
. (14)
Спектры планов можно изобразить в привычной для экспериментатора табличной форме таблица 14.
| № | Зазор рабочей области | Частота входного сигнала | Расход топлива на 100 км. |
| 1 | 20мм | 200 Гц | 6,58 |
| 2 | 40мм | 200 Гц | 6,21 |
| 3 | 20мм | 400Гц | 5,75 |
| 4 | 40мм | 400Гц | 5,32 |
Опыты при выполнении эксперимента проводятся в последовательности, предусмотренной матрицей плана.
Прежде чем определить оценки коэффициентов регрессии, необходимо выполнить статистический анализ результатов эксперимента с целью оценки их качества и пригодности для построения регрессионной модели. Статистический анализ включает оценку ошибок параллельных опытов, отсеивание грубых ошибок, проверку однородности дисперсий опытов и определение дисперсии воспроизводимости эксперимента.
Ошибки параллельных опытов. В условиях наличия случайных помех с целью уменьшения случайных погрешностей эксперимента и повышения точности получаемой регрессионной модели осуществим дублирование опытов, т. е. проведем параллельные опыты. Каждый опыт, предусмотренный матрицей спектра плана, повторяется т = 3 раза.
Следовательно, необходимо проводить L=Nm=24 опыта, в соответствии с матрицей плана, предусматривающей при этом рандомизацию опытов.
Для выбора случайной последовательности опытов используем таблицу равномерно распределенных случайных чисел. Первое число таблицы выберем произвольно, случайным образом (число 46), а затем, начиная с этого числа, выписываем 24 числа таблицы. При этом числа, больше 24, а так же уже выписанные, отбрасываем. Последовательность проведения опытов следующая: 16,08,23,03,14,10,19,15,04,12,07,11,20,21,17,01,18,13,22,24,02,05,06,09. В опытах 6,10,17,23 - проведена рандомизация внесением систематической инструментальной погрешности. В остальных опытах были учтены границы суммарной погрешности определенной в каждой точке плана. Повторные опыты в одной и той же точке плана при наличии помехи дают различные результаты при определении функции отклика. Разброс результатов относительно оценки математического ожидания функции отклика надо оценить.
Для каждой точки плана по результатам параллельных опытов находим выборочное среднее[5]:
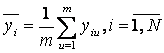 , (15)
, (15)
где u –номер параллельного опыта; ![]() - значение функции отклика в u-м параллельном опыте i-ой точки спектра плана. Для удобства составим таблицу 15.
- значение функции отклика в u-м параллельном опыте i-ой точки спектра плана. Для удобства составим таблицу 15.
| № | Зазор рабочей области |
Частота входного сигнала |
Расход топлива на 100 км. |
| 1 | 20мм | 180 Гц | 6,67 |
| 2 | 20мм | 220 Гц | 6,51 |
| 3 | 20мм | 200Гц | 6,6 |
| 4 | 40мм | 200Гц | 6,22 |
| 5 | 40мм | 180 Гц | 6,3 |
| 6 | 40мм | 220 Гц | 6,15 |
| 7 | 20мм | 380Гц | 5,82 |
| 8 | 20мм | 450 Гц | 5,72 |
| 9 | 20мм | 420 Гц | 5,65 |
| 10 | 40мм | 380Гц | 5,45 |
| 11 | 40мм | 450 Гц | 5,35 |
| 12 | 40мм | 420 Гц | 5,25 |
Построим таблицу для нахождения выборочной средней для каждой точки плана.
| № | |||||
| 1 | 6,60 | 6,68 | 0,08 | 0,007 | 0,007 |
| 2 | 6,60 | 6,51 | -0,09 | 0,008 | 0,007 |
| 3 | 6,60 | 6,6 | 0,00 | 0.00 | 0,007 |
| 4 | 6,22 | 6,22 | 0,00 | 0,000 | 0,003 |
| 5 | 6,22 | 6,3 | 0,08 | 0,006 | 0,003 |
| 6 | 6,22 | 6,15 | -0,07 | 0.00 | 0,003 |
| 7 | 5,72 | 5,82 | 0,0967 | 0,009 | 0,0075 |
| 8 | 5,72 | 5,72 | -0,0233 | 0,001 | 0,0075 |
| 9 | 5,72 | 5,65 | -0,0733 | 0,005 | 0,0075 |
| 10 | 5,35 | 5,45 | 0,1000 | 0,010 | 0,010 |
| 11 | 5,35 | 5,35 | 0,0000 | 0,000 | 0,010 |
| 12 | 5,35 | 5,25 | -0,1000 | 0,010 | 0,010 |
Для оценки отклонения функции отклика от ее среднего значения ![]() вычисляем дисперсию воспроизводимости опыта по данным т=3 параллельных опытов в каждой i-ой точке спектра плана
вычисляем дисперсию воспроизводимости опыта по данным т=3 параллельных опытов в каждой i-ой точке спектра плана
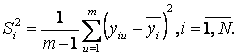 (16)
(16)
При вычислении ![]() принимают число степеней свободы k = т –1=2, так как одна степень свободы уже использована для вычисления
принимают число степеней свободы k = т –1=2, так как одна степень свободы уже использована для вычисления ![]() . Это обеспечивает несмещенность оценки дисперсии воспроизводимости опыта
. Это обеспечивает несмещенность оценки дисперсии воспроизводимости опыта ![]() . Вычисления приводятся в таблице 15.
. Вычисления приводятся в таблице 15.
Отсеивание грубых ошибок.
Используем t-критерий Стьюдента
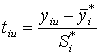 . (17)
. (17)
Полученное значение t-критерия сравниваем с табличным tт=4,3 при выбранном уровне значимости ![]() и числе степеней свободы k=2 Получаем t < tт, это означает, что результаты опытов могут быть использованы.
и числе степеней свободы k=2 Получаем t < tт, это означает, что результаты опытов могут быть использованы.
Проверка однородности дисперсий. Однородность дисперсии означает, что среди всех дисперсий ![]() нет таких, которые бы значительно превышали все остальные. Для проверки однородности дисперсий во всех точках спектра плана используется либо критерий Кохрена G, либо критерий Фишера F..
нет таких, которые бы значительно превышали все остальные. Для проверки однородности дисперсий во всех точках спектра плана используется либо критерий Кохрена G, либо критерий Фишера F..
Критерий Кохрена основан на распределении отношения максимальной дисперсии ![]() к сумме всех дисперсий
к сумме всех дисперсий
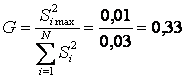 . (18)
. (18)
Критерий Кохрена применяется, если количество сравниваемых дисперсий больше двух, а число повторных опытов во всех точках плана одинаково. Определив число степеней свободы k1 = т –1=2 и k2 = 8 (N — число точек спектра плана, т — количество повторных опытов в каждой точке плана), находят табличное значение критерия Кохрена GТ=0,5157. Так как G< GТ, гипотеза об однородности дисперсий и воспроизводимости результатов принимается. В этом случае каждая из дисперсий ![]() оценивает одну и ту же дисперсию помехи
оценивает одну и ту же дисперсию помехи ![]() . Следовательно, полученные результаты эксперимента качественные и могут быть использованы для построения регрессионной модели.
. Следовательно, полученные результаты эксперимента качественные и могут быть использованы для построения регрессионной модели.
Критерий Фишера можно применять при любом числе дисперсий ![]() . Он определяется из соотношения
. Он определяется из соотношения
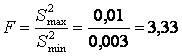 . (19)
. (19)
Дисперсии однородны, так как F < Fт , где FТ=9,28 — табличное значение критерия Фишера, определяемое при числах степеней свободы k1 и k2 и принятом уровне значимости q.
Следует отметить, что уровень значимости q по всем критериям, применяемым в процессе статистического анализа и обработки результатов эксперимента (Кохрена, Стьюдента, Фишера), должен быть одинаков. Для технических систем рекомендуется принимать q = 0,05.
Дисперсия воспроизводимости эксперимента. Если дисперсии ![]() однородны, то их усредняют и находят дисперсию воспроизводимости эксперимента
однородны, то их усредняют и находят дисперсию воспроизводимости эксперимента
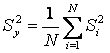 =
=![]() . (20)
. (20)
Дисперсия ![]() представляет собой оценку дисперсии помехи
представляет собой оценку дисперсии помехи ![]() .
.
Определение коэффициентов регрессионной модели и проверка их значимости.
Параметрами регрессионной модели являются коэффициенты регрессии bj, ![]() , где NВ =4 — количество базисных функций. Значения коэффициентов регрессии можно получить, решив систему алгебраических уравнений.
, где NВ =4 — количество базисных функций. Значения коэффициентов регрессии можно получить, решив систему алгебраических уравнений.
![]()
![]()
 .
.
![]()
Так как информационная матрица Фишера Ф для ПФЭ (полного факторного эксперимента) и ДФЭ (дробного факторного диагональная и все диагональные элементы ее одинаковы и равны N, то выражение для определения всех коэффициентов уравнения регрессии одинаково и имеет простой вид:
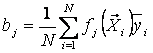 , (22)
, (22)
где N — число точек спектра плана; ![]() — значение j-ой базисной функции в i-ой точке спектра плана;
— значение j-ой базисной функции в i-ой точке спектра плана; ![]() — выборочное среднее функции отклика в той же точке, определяемое по формуле (15).
— выборочное среднее функции отклика в той же точке, определяемое по формуле (15).
Значения базисных функций ![]() для отдельных факторов равны Хij, а для взаимодействия факторов — XikXilXim … . С учетом этого на основе выражения (22) можно записать следующие формулы для вычисления значений коэффициентов уравнения регрессии:
для отдельных факторов равны Хij, а для взаимодействия факторов — XikXilXim … . С учетом этого на основе выражения (22) можно записать следующие формулы для вычисления значений коэффициентов уравнения регрессии:
для коэффициентов при факторах xj, включая также свободный член уравнения
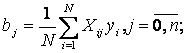 (23)
(23)
для коэффициентов при взаимодействиях факторов
![]()
![]() (24)
(24)
где n — количество факторов.
Для плана ПФЭ N = 2п. При определении коэффициента b0 (свободного члена уравнения регрессии) Xi0 =1, i = ![]() .
.
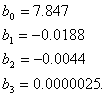
Поскольку полученные значения коэффициентов регрессии bj, ![]() — случайные числа, в связи с действием случайной помехи в процессе эксперимента, то они являются оценками истинных значений коэффициентов регрессии βj . Погрешность определения bj оценивают дисперсией
— случайные числа, в связи с действием случайной помехи в процессе эксперимента, то они являются оценками истинных значений коэффициентов регрессии βj . Погрешность определения bj оценивают дисперсией ![]() .
.
Дисперсии ![]() оценок всех коэффициентов регрессии одинаковы. Величина дисперсии
оценок всех коэффициентов регрессии одинаковы. Величина дисперсии ![]() зависит только от ошибки воспроизводимости эксперимента
зависит только от ошибки воспроизводимости эксперимента ![]() и числа опытов
и числа опытов
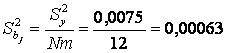 , (25)
, (25)
где т — число повторных опытов (значение т должно быть одинаковым для всех точек N спектра плана).
После определения коэффициентов регрессии bj проверяют их значимость. Эта проверка осуществляется с использованием t-критерия Стьюдента, значение которого находят из соотношения
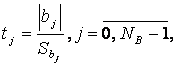 (26)
(26)
где NB — общее число коэффициентов уравнения регрессии, равное количеству используемых базисных функций для построения регрессии.
Полученное значение tj для каждого коэффициента регрессии b] сравнивают с табличным tт, определяемым при принятом уровне значимости q и числе степеней свободы k = N(m - 1), с которым определялась дисперсия воспроизводимости ![]() . Если tj < tт, нулевая гипотеза о незначимости коэффициента bj принимается и член уравнения регрессии, включающий этот коэффициент, исключается из математической модели. Если же tj< tт, полагают, что данный коэффициент значимо (неслучайно) отличается от нуля и его следует сохранить в регрессионной модели. В этом случае значение коэффициента bj больше ошибки опыта, которую можно оценить величиной доверительного интервала
. Если tj < tт, нулевая гипотеза о незначимости коэффициента bj принимается и член уравнения регрессии, включающий этот коэффициент, исключается из математической модели. Если же tj< tт, полагают, что данный коэффициент значимо (неслучайно) отличается от нуля и его следует сохранить в регрессионной модели. В этом случае значение коэффициента bj больше ошибки опыта, которую можно оценить величиной доверительного интервала ![]() . Доверительный интервал находят по формуле
. Доверительный интервал находят по формуле ![]() =
=![]() (27)
(27)
Следует, однако, отметить, что дисперсия воспроизводимости эксперимента ![]() зависит от очень многих факторов: выбора центра эксперимента, интервалов варьирования факторов, наличия экстремумов функции отклика в области планирования, соотношения величины отклика и помехи (так называемое отношение сигнал-шум) и др. В этой связи при небольшом различии между tj, и tТ следует весьма осторожно относиться к оценке значимости коэффициентов регрессии. Лучше такие коэффициенты сохранить в модели, а влияние соответствующего фактора (или взаимодействия факторов) проверить в дальнейшем на более сложной модели или в иных условиях планирования эксперимента.
зависит от очень многих факторов: выбора центра эксперимента, интервалов варьирования факторов, наличия экстремумов функции отклика в области планирования, соотношения величины отклика и помехи (так называемое отношение сигнал-шум) и др. В этой связи при небольшом различии между tj, и tТ следует весьма осторожно относиться к оценке значимости коэффициентов регрессии. Лучше такие коэффициенты сохранить в модели, а влияние соответствующего фактора (или взаимодействия факторов) проверить в дальнейшем на более сложной модели или в иных условиях планирования эксперимента.
После исключения незначимых коэффициентов уравнение регрессии приобретает вид:
![]() . (28)
. (28)
Сформируем остаточную последовательность (ряд остатков), для чего из фактических значений уровней ряда вычтем соответствующие расчетные значения по модели (28):
Таблица. 17
| t | Фактор |
Решение |
Отклонение |
Точки пиков | ( |
|||
| 1 | 6,67 | 6,6805 | -0,00050 | - | 2,5E-07 | - | 0,007 | |
| 2 | 6,51 | 6,5045 | 0,18050 | 1 | 0,03258 | 0,18 | 0,032761 | 2,700 |
| 3 | 6,6 | 6,5925 | -0,08250 | 1 | 0,00681 | -0,26 | 0,069169 | 1,267 |
| 4 | 6,22 | 6,1295 | 0,46800 | 1 | 0,21902 | 0,55 | 0,30305 | 7,094 |
| 5 | 6,3 | 6,3055 | -0,17050 | 1 | 0,02907 | -0,64 | 0,407682 | 2,779 |
| 6 | 6,15 | 6,2175 | 0,09250 | 1 | 0,00856 | 0,26 | 0,069169 | 1,466 |
| 7 | 5,82 | 5,8005 | 0,33450 | 1 | 0,11189 | 0,24 | 0,058564 | 5,452 |
| 8 | 5,72 | 5,7125 | 0,09750 | 1 | 0,00951 | -0,24 | 0,056169 | 1,678 |
| 9 | 5,65 | 5,6245 | 0,09800 | - | 0,0096 | 0,00 | 2,5E-07 | 1,713 |
| 10 | 5,45 | 5,4255 | 0,20950 | 1 | 0,04389 | 0,11 | 0,012432 | 3,718 |
| 11 | 5,35 | 5,3375 | 0,09750 | 1 | 0,00951 | -0,11 | 0,012544 | 1,794 |
| 12 | 5,25 | 5,2495 | 0,09800 | - | 0,0096 | 0,00 | 2,5E-07 | 1,833 |
Проведем проверку случайности уровней ряда остатков на основе критерия пиков.
Уровень последовательности ![]() считается максимумом, если он больше двух рядом стоящих уровней, т.е.
считается максимумом, если он больше двух рядом стоящих уровней, т.е. ![]() , и минимумом, если он меньше обоих соседних уровней, т.е.
, и минимумом, если он меньше обоих соседних уровней, т.е. ![]() .В обоих случаях
.В обоих случаях ![]() считается поворотной точкой; общее число поворотных точек для остаточной последовательности
считается поворотной точкой; общее число поворотных точек для остаточной последовательности ![]() обозначим через p.
обозначим через p.
В случайной выборке математическое ожидание числа точек поворота ![]() и дисперсия
и дисперсия ![]()
![]() выражаются формулами:
выражаются формулами:
![]() =
=![]() ,
, ![]()
Критерий случайности с ![]() =5% уровнем значимости, является выполнение неравенства
=5% уровнем значимости, является выполнение неравенства
Это неравенство выполняется, проверенная модель считается адекватной
![]() .
.
Проверка соответствия распределения случайной компоненты нормальному закону распределения ![]() -критерий.
-критерий.
Этот критерий численно равен отношению размаха вариации случайной величины ![]() к стандартному отклонению
к стандартному отклонению ![]() .
.
![]() ;
;
![]()
значение ![]() -критерия сравнивается с табличными верхними и нижними границами данного отношения, и если это значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается, в противном принимается [4].
-критерия сравнивается с табличными верхними и нижними границами данного отношения, и если это значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается, в противном принимается [4].
Т.к. при ![]()
![]() нижняя граница равна 2, 67 , а верхняя граница равна 3,685.
нижняя граница равна 2, 67 , а верхняя граница равна 3,685.
![]() .
.
![]() .
.
![]() характеризует нормальное распределение, т.к. 2,76<3,022<3,685.
характеризует нормальное распределение, т.к. 2,76<3,022<3,685.
Проверим гипотезу о равенстве математического ожидания случайной компоненты нулю:
Расчетное значения ![]() - критерия Стьюдента
- критерия Стьюдента ![]() =1,944, где
=1,944, где ![]() среднее арифметическое значение уровней
среднее арифметическое значение уровней![]() ,
, ![]() -СКО
-СКО ![]() . Так как расчетное 1,944<2.18 c заданным
. Так как расчетное 1,944<2.18 c заданным ![]() и числом степеней свободы
и числом степеней свободы ![]() , то гипотеза о равенстве математического ожидания нулю принимается.
, то гипотеза о равенстве математического ожидания нулю принимается.
Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности. Расчетное значение ![]() - критерия Дарбина – Уотсона.
- критерия Дарбина – Уотсона.
 .
.
Если![]() в интервале от 2 до 4 то связи отрицательны, в этом случае преобразуется в
в интервале от 2 до 4 то связи отрицательны, в этом случае преобразуется в ![]() и в дальнейшем используем
и в дальнейшем используем ![]() .
.
Расчетное ![]() сравнивается с
сравнивается с ![]() и
и ![]() критические значениями статистики Дарбина – Уотсона.
критические значениями статистики Дарбина – Уотсона.
| n | |
|
|
|||
| 15 | 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 |
| 20 | 1,20 | 1,41 | 1,10 | 1,54 | 1,00 | 1,68 |
| 30 | 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 |
Если ![]() , то автокорреляции нет. Если
, то автокорреляции нет. Если ![]() , то модель неадекватна. Если
, то модель неадекватна. Если ![]() , то стоп, исследования не продолжать. Т.к.
, то стоп, исследования не продолжать. Т.к. ![]() , то автокорреляция наблюдается, поэтому переходим к расчетам по
, то автокорреляция наблюдается, поэтому переходим к расчетам по ![]() , сравниваем с
, сравниваем с ![]() т.к.
т.к. ![]() ,то делаем вывод: уровни независимы.
,то делаем вывод: уровни независимы.
Остаточная последовательность удовлетворяет всем свойствам случайной компоненты ряда, следовательно, модель адекватна.
Для характеристики точности модели воспользуемся средней относительной ошибкой аппроксимации.
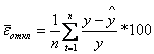 ,
,
![]() = 1,94%.
= 1,94%.
Полученное значение средней относительной ошибки говорит о достаточно высоком уровне точности построенной модели, ошибка менее 5% свидетельствует об удовлетворительном уровне точности. Для адекватной модели показателем точности является коэффициент сходимости:
 =0,1896 и коэффициент детерминации
=0,1896 и коэффициент детерминации ![]() =0,8107.
=0,8107.
Заключение.
Результаты исследований обработки жидкого топлива показали, что применение одновременной обработки магнитным и акустическим полем дают возможность увеличить степень сгорания топлива, и как следствие уменьшить расход топлива. Построенная модель позволяет выбрать оптимальные параметры АМА для конкретного типа автотранспорта.
Литература
1. Пустовалов Г.Е., Талалаева Е.В. Простейшие физические измерения и их обработка. – М.: МГУ, -1967.
2.Тарасик В.П. Математическое моделирование технических систем / В.П. Тарасик.- Мн.: ДизайнПРО, 1997.
3. Сергеев А.Г., Латышев М.В. Терегеря В.В. Метрология, стандартизация, сертификация: Учебное пособие. – М.: Логос, 2003. – 536 с.
4. Тойберт П. Оценка точности результатов измерений: Пер. с нем. – М.: Энергоатомиздат, 1988.
5. Ермаков С.М., Жиглявский А.А. Математическая теория оптимального эксперимента: Учеб. пособие. – М.: Гл. ред. физ.-мат. лит.,1987. – 320 с.
Научный электронный журнал КубГАУ . № 02(4), 2004