Научный электронный журнал КубГАУ . № 01(3), 2004

СТРУКТУРА 2 ПРОИЗВОДСТВЕННОЙ СИСТЕМЫ С ВЕРТИКАЛЬНОЙ ИНТЕГРАЦИЕЙ

Крохмаль В.В. – к. э. н., профессор

Лойко В.И.– д. т. н., профессор

Кубанский государственный аграрный университет

В статье проводится исследование на эффективность и устойчивость возможной структуры вертикально-интегрированных систем, названной авторами структура 2.

Для исключения недостатков структуры 1 (см. статью «Структура 1 производственной системы с вертикальной интеграцией») может быть предложена структура 2 системы с вертикальной интеграцией, в которой существенно изменены направления материальных и денежных потоков (рис. 1) [1].

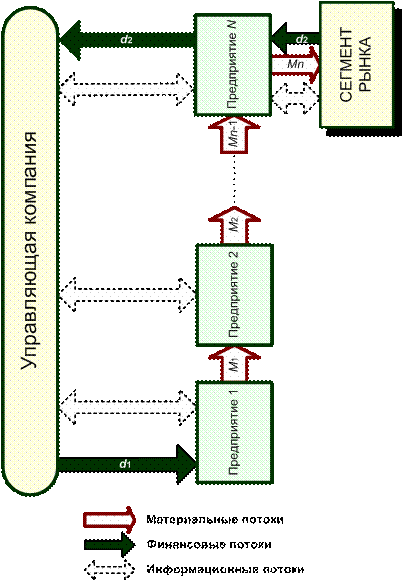
Рис. 1. Структура 2 системы с вертикальной интеграцией

Введенные в схему изменения наиболее полно охватывают технологический процесс производства и минимизируют материально-денежные потоки, что, в свою очередь, существенно снижает влияние времени прохождения денежных средств на производство.

Однонаправленные материальные потоки действуют только между производственным предприятием 1 и предприятием N, реализующим готовую продукцию переработки на рынке, не затрагивая управляющую компанию, что уменьшает транспортные расходы и ускоряет переработку материальных производственных ресурсов между предприятиями (см. рис. 1).

Отсутствие возникновения дополнительных денежных потоков между звеньями технологической цепочки способствует ритмичной работе отдельных производств и всей системы в целом. В ней действуют только два денежных потока: от управляющей компании к предприятию 1 (поток d₁) и от предприятия N к управляющей компании после реализации товара на рынке (поток d₂). Такая организация денежных потоков снижает их влияние на внутренний цикл производства, что очень важно в современных условиях.

Двунаправленные информационные потоки блоков системы объединяются через управляющую компанию, и вся экономическая, технологическая, финансовая и транспортная информация с учетом внешнего информационного потока (о ценах, рынках, налогах и т.д.) накапливается и перерабатывается в одном месте, что увеличивает ее эффективность.

Функционирование системы организовано следующим
образом [1]. На основе анализа и синтеза информации о потребностях рынка, ценах, технологических и технических возможностях производств и других данных определяется объем денежных средств d₁, необходимый для закупки у предприятия 1 количества исходного материального ресурса, достаточного для завершения технологического цикла.

При этом учитывается, что прибыль каждого этапа реинвестируется в увеличение соответствующего материального потока.

При исследовании структуры 2 системы с вертикальной интеграцией будем, как и при анализе структуры 1, считать норму прибыли одинаковой для всех предприятий, входящих в объединение, и равной k. Это возможно, если с точки зрения формы собственности, предприятия структуры образуют холдинг. Действительно, холдинговая организация дает больший синергический эффект и более чувствительна к управляющим воздействиям головной компании.

Эффективность структуры 2

На первом этапе объем закупленного ресурса М₁ эквивалентен денежным средствам d₁ плюс прибыль первого этапа kd₁, т.е.

М₁~ (1+k) d₁.

Соответственно материальный поток М₂ эквивалентен
(1 + k) М₁ или

М₂ ~ (1 + k)² d_1.

Поток М₃ будет эквивалентен (1 + k) М₂, поток М₄ – соответственно (1+ +k) М₃ и т. д. После реализации на рынке товарного потока М_n  ~ (1 + k)ⁿ d₁ выручка составит

B = d₂ = (1 + k)ⁿ d₁. 

Так же, как и в структуре 1, в зависимости от вида технологии переработки и ее организации, в течение исследуемого периода (например, года) возможно несколько циклов производства (многократное прохождение технологической цепочки). Если обозначить число циклов в исследуемый период через m, то формула для определения выручки примет вид

B = m (1 + k)ⁿ d₁. (1)

Обозначим через ρ долю от d₁ дополнительных расходов на организацию производственного процесса в одном цикле (оплата труда, амортизация основных средств и т. п.). В этом случае общие расходы за период составят

P = d₁ + mρd₁ = d₁ (1 + mρ). (2)

Тогда чистый доход определим следующим образом:

D = B – P. 

Используя выражения (1) (2) и проведя ряд преобразований, получим чистый доход, выраженный через исходный денежный поток, коэффициент прибыли (норму прибыли), число этапов (ступеней) технологической цепочки и количество циклов за период:

D = d₁ [m (1 + k)ⁿ – (1 + mρ)].  (3)

Эффективность интегрированной системы, имеющей структуру 2, определим как

.  (4)

Из выражения (4) видно, что эффективность структуры 2 системы с вертикальной интеграцией, в отличие от структуры 1, нелинейно зависит от всех четырех аргументов (факторов), что отражено на рисунках 2, 3 и 4 и 5. Графики наглядно показывают, что эффективность структуры 2 выше, чем структуры 1.

Сравнительная эффективность и устойчивость структуры 2

Сравним эффективность структуры 2 с этим же показателем структуры 1 (см. статью «Структура 1 производственной системы с вертикальной интеграцией»). Для этого введем коэффициент сравнительной эффективности Э, представляющий собой отношение эффективности структуры 2 к эффективности структуры 1:

,

где E₂ – эффективность структуры 2; E₁ – эффективность структуры 1.

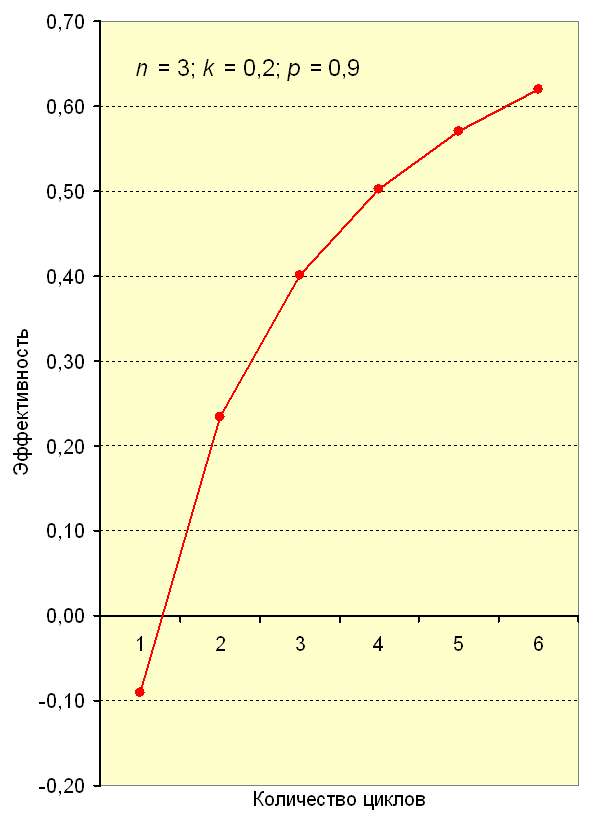
Рис. 2. Зависимость эффективности структуры 2 от количества циклов

за период при n = 3; k = 0,2; ρ = 0,9

Рис. 3. Зависимость эффективности структуры 2 от доли затрат ρ

и количества циклов за период m при n = 3; k = 0,3

Рис. 4. Зависимость эффективности структуры 2 от нормы прибыли k и

количества ступеней n технологического цикла при m = 1; ρ = 0,5

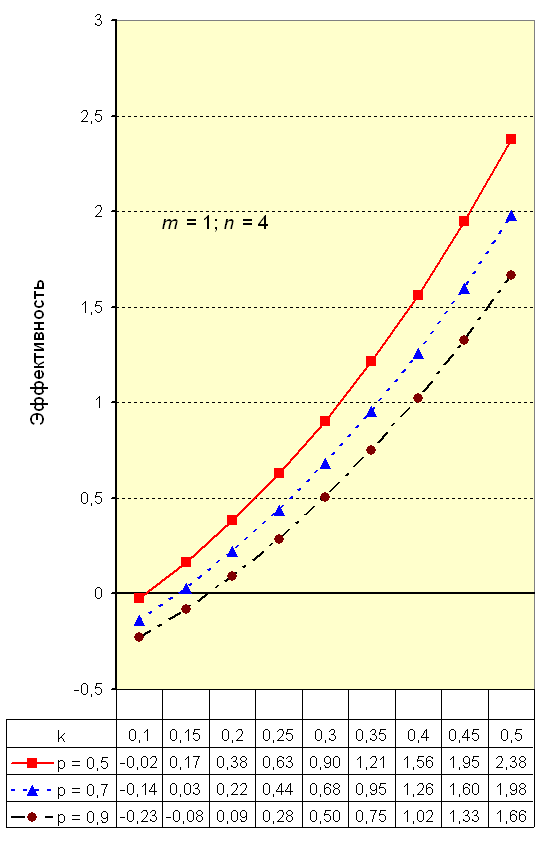
Рис. 5. Зависимость эффективности структуры 2 от нормы прибыли k

и доли расходов ρ при m = 1; n = 4

Для уравнивания условий предположим, что доля расходов ρ и исходные денежные средства d₁ в обеих схемах одинаковы. Тогда коэффициент сравнительной эффективности Э может быть определен как

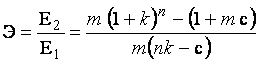. (5)

На рисунках 6–8 приведены графики зависимостей эффективностей E₂, E₁ и коэффициента сравнительной эффективности Э от нормы прибыли для трех значений доли расходов при фиксированных значениях количества циклов и числа предприятий в технологической цепочке. При этом наблюдается интересная закономерность, связанная с тем, что нелинейность E₂ выражена сильнее, чем E₁:

- при возрастании доли расходов E₂ и E₁ в целом уменьшаются, но с разной скоростью, что приводит к общему росту коэффициента сравнительной эффективности Э;

- при значениях E₁ < 0,1 наблюдается резкий рост Э, что подтверждает большую степень эффективности и устойчивости структуры 2 по сравнению со структурой 1 при равных условиях в области указанных значений E₁.

Границу устойчивости структуры 2 определим из тех же соображений, что и для структуры 1.

Типовые показатели устойчивости предприятий – это 3, 4 и 5-й уровни самосохранения, на которых значение параметра самосохранения лежит в диапазоне от С_Сmin = 0 до С_Сmax = 2.

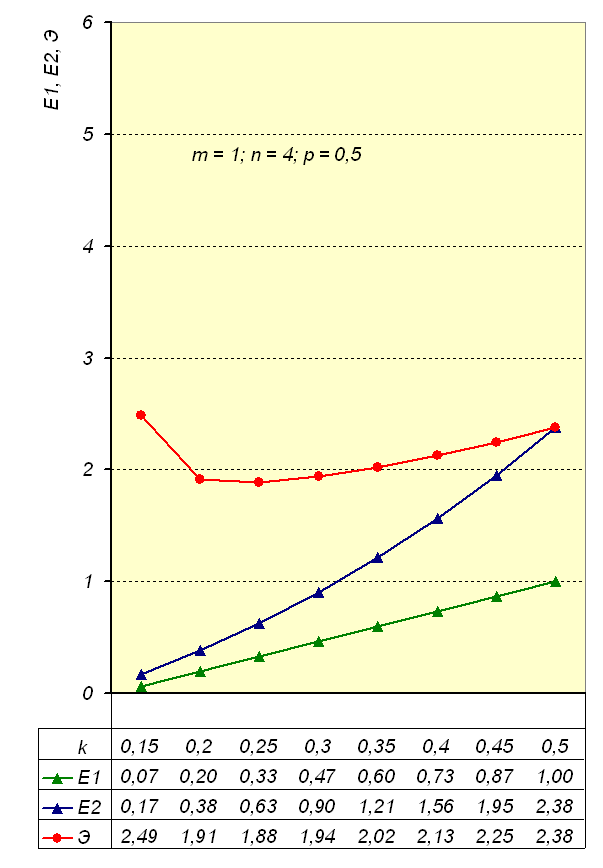
Рис. 6. Кривые зависимостей E₂, E₁ и Э от n
при m =1, n = 4, ρ = 0,5

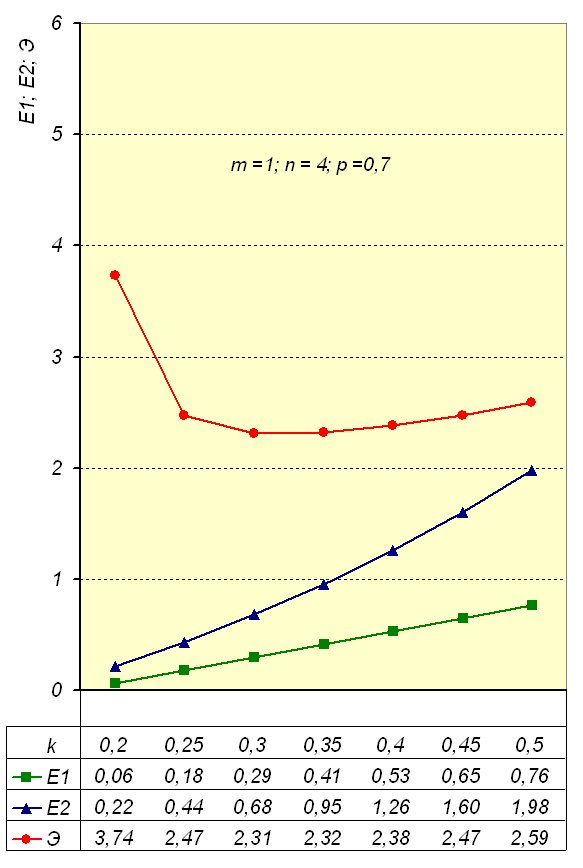
Рис. 7. Кривые зависимостей E₂, E₁ и Э от n
при m =1, n = 4, ρ = 0,7

Рис. 8. Кривые зависимостей E₂, E₁ и Э от n
при m =1, n = 4, ρ = 0,9

На этих уровнях параметр самосохранения эквивалентен принятому в работе показателю эффективности деятельности предприятия E. Тогда для структуры 2, c учетом значения нижней границы параметра самосохранения, можно записать

. (6)

Из выражения (6) следует, что для устойчивого функционирования структуры 2 необходимо выдерживать следующее соотношение параметров k, n, m и ρ:

. (7)

Увеличение значений левой части неравенства (7) свидетельствует о снижении риска потери устойчивости интегрированной системой.

Если сравнить (7) с условием сохранения устойчивости в структуре 1, то видно, что в структуре 1 на нижний предел устойчивости системы значение количества циклов m оборота финансового потока d₁ не влияет, что снижает возможность управления ситуацией в этой системе.

Таким образом, сравнительный анализ исследуемых структур показывает, что структура 2 обладает большей эффективностью и устойчивостью по сравнению со структурой 1. Однако сравнение проводилось в предположении, что обе структуры имеют холдинговую организацию и, как следствие, равные для всех входящих в холдинг предприятий показатели нормы прибыли и доли расхода. Если исследуемые структуры будут формироваться не на основе преобладающей собственности (контрольный пакет акций), а с использованием других форм отношений (договора, контракты, соглашения), то модели, описывающие функционирование рассмотренных структур, усложнятся. Это приведет к усложнению управления системой и к снижению эффективности и запаса устойчивости структур.

Список литературы

1. Лойко В.И. Методическое обеспечение структурной перестройки предприятий агропромышленного комплекса в переходный период. Краснодар: КубГАУ, 2000. 226 с.

2. Смирнов Э.А. Теория организации: Учеб. пособие. М.: ИНФРА-М, 2003. 248 с.

Научный электронный журнал КубГАУ . № 01(3), 2004