Научный электронный журнал КубГАУ . № 02(2), 2003
УДК 536.5
О ТЕРМОДИНАМИКЕ ИЗЛУЧЕНИЯ И ВЗАИМОСВЯЗИ ПОЛЕЙ
Агеев Ю.М. – д.т.н., профессор
Кубанский государственный аграрный университет
В статье установлены новые эквиваленты взаимосвязей различных по природе физических явлений. Получен закон Ома для стационарных электрического и магнитного полей в дифференциальной форме, включающий волновое сопротивление вакуума. На основе непланковского подхода (без представлений о квантовости) выведен закон спектрального излучения черного тела. Впервые приведены уравнение и график диаграммы состояния поля излучения. Полученные результаты углубляют известные данные об аналогии как стационарных, так и динамических электрических, магнитных, гравитационных и механических явлений. Выявлена общность квадратичной зависимости от скорости движения в рассмотренных явлениях.
I. Большой интерес представляет разработка основных положений теории равновесного поля излучения. Полученные автором результаты впервые дали возможность получить уравнение адиабаты поля излучения в форме, содержащей температуру как параметр, и вывести закон Стефана – Больцмана нетрадиционным путем.
1. В. Вин при адиабатическом изменении объема поля излучения на базе первого закона термодинамики
dA= –dЭл (1.1)
PdV= –dЭл (1.2)
обнаружил, что вследствие изотропности поля излучения при термодинамическом равновесии давление лучей равно трети объемной плотности энергии излучения
P = uл/3 = (1/3)Эл/Vл , (1.3)
где Uл = Эл / Vл – объемная плотность энергии Эл поля излучения в объеме Vл.
Подставив уравнение (1.3) в (1.2), получаем
. (1.4)
Интегрируя выражение (1.4), находим
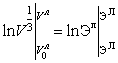(1.5)
(1.6)
или, подставив 
и 
, получаем уравнение адиабаты поля излучения, связывающее
объемную плотность его энергии и объем:
.
(1.7)
Учитывая связь плотности энергии поля излучения с давлением его лучей, запишем уравнение адиабаты поля изучения, связывающее давление и объем:
(1.8)
или
, (1.9)
где 
– показатель
адиабаты равновесного поля излучения.
2. В отличие от известных схем Л. Больцмана, В. Вина, Бартоли, Б. Голицина и др. допустим, что в некоторой полости, идеально изолированной от внешней среды, находится идеальный газ, молекулы которого не способны излучать под некоторой бесконечно тонкой, с высокой теплопроводностью оболочкой, которая является неупругой, идеально разделяющей газ и поле излучения, идеально белой со стороны газа и идеально черной – поля излучения.
Допустим, в принятой нами системе газ – поле произошел переход
в газе от параметров 
к параметрам 
. Это было условное расширение, при котором газ совершает
работу за счет уменьшения своей внутренней энергии:
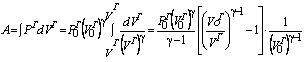(1.10)
Для идеального газа уравнение адиабаты примет вид:
, (1.11)
отсюда
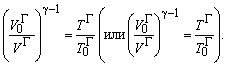(1.12)
Подставляя соотношение (1.12) в (1.10), получим работу газа
, (1.13)
где
; 
; (1.14)
(1.15)
и 
– энергия газа, определяемая количеством n молей, при
температуре Т в адиабатических условиях.
В изолированной системе газ – поле изменение внутренней энергии газа равно изменению внутренней энергии поля излучения, т.к. только здесь поле излучения и вещество газа могут обмениваться энергией:
. (1.16)
Для 
имеем
. (1.17)
Из равенства (1.17) следует: если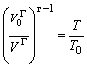 
(по уравнению адиабаты газа), то должно выполняться
аналогичное для поля излучения условие:
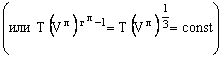. (1.18)
Этот результат получен прямым путем на базе классической термодинамики взаимодействия вещества газа и поля излучения в единой изолированной системе без учета закона Стефана – Больцмана.
В результате впервые показано, что уравнение адиабаты поля излучения можно было найти по Г. Кирхгофу, тем более Вину, не опираясь на закон Стефана.
3. Обращаясь к уравнению адиабаты поля излучения (1.7) и к формуле (1.18), получаем систему:
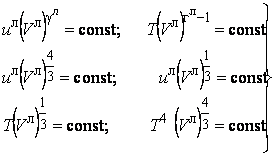. (1.19)
Разделив первое уравнение на второе, находим связь объемной плотности поля излучения и температуры в условиях термодинамического равновесия:
. (1.20)
Полученное уравнение адиабаты поля равновесного излучения является общеизвестным законом Стефана – Больцмана.
Однако в отличие от известных работ Стефана, Больцмана, Вина, Планка и др., нами оно выведено с помощью инструментов классической термодинамики и, по нашему убеждению, могло быть найдено еще 150 лет назад во времена Г. Кирхгофа.
4. Представим уравнение адиабаты равновесного поля изучения в виде зависимости давления и температуры:
, (1.21)
где 
– соотношение констант в последней форме адиабаты равновесного
поля излучения при параллельных лучах, направленных нормально
к площадке лучеприемника, и при диффузном характере излучения,
когда яркость лучей одинакова по всем направлениям.
5. Полученные разные виды уравнения адиабаты равновесного поля излучения позволяют установить уравнение состояния поля излучения:
, (1.22, а)
,
(1.22,б)
. (1.22, в)
Преобразуем уравнение (1.22, а), выразив через объем 
поля:
.
(1.23)
Далее в результате замены члена 
,
имеем
,
(1.24)
где 
– универсальная постоянная равновесного интегрального
поля излучения, 
:
,
где 
.
Итак, из расчета для нормального объема пространства (
), занимаемого равновесным полем излучения, получаем
величину 
универсальной постоянной поля излучения
произвольного объема и
давления излучения 
(или
объемной плотности 
энергии
поля излучения), равную, более точно
.
Окончательно уравнение состояния равновесного поля излучения имеет вид
.
Если поле излучения находится под поршнем при неизменном давлении 
, то, следовательно, и при постоянной температуре
стенок Т=const (особенность поля излучения) давление
равновесного излучения через константу пропорционально четвертой
степени абсолютной температуры. В случае с газом (P=n k T)
давление газа через константу пропорционально произведению
концентрации микрочастиц газа на абсолютную температуру, т.е.
связано с объемом и температурой одновременно. Таким образом,
осуществить изобарический процесс с полем излучения при изменяющейся
температуре стенок полости, терморавновесных с полем, невозможно.
Отсюда следует соответствующий физический смысл универсальной
постоянной равновесного поля излучения: 
–
это удельная объемная плотность энергии поля излучения, которая
прибавляется на единицу объема поля при изменении на 1К температуры
стенок полости, ограничивающих поле в условиях термодинамического
равновесия.
Изменение температуры на 1К приводит к изменению давления пропорционально четвертой степени температуры и соответственно объема – обратно пропорционально третьей степени температуры.
Поэтому при переменной температуре изо6арические и изохорические процессы с полем излучения невозможны.
II. Вывод формулы М. Планка не предполагает использования допущения по квантовости излучения. Один из возможных путей ее получения без использования планковских квантов рассмотрим применительно к равновесному полю излучения.
1. В цилиндрической полости с площадью поперечного сечения 1м2 под поршнем находится в вакууме движущаяся вдоль оси симметрии монохроматическая плоскополяризованная электромагнитная волна (МПП ЭМВ), которая существует там сколь угодно долго вследствие идеально отражающих внутренних поверхностей в виде стоячей волны, узлы и пучности которой расположены вдоль полости. Допустим, что длина полости равна пути, проходимому МПП ЭМВ за 1с,: х0 = С×1с = С [м]. При этом на этой длине полости укладывается число мод (целых волн длиной l0 ): N0 = n = C/l0 с энергией Э0, где n – частота колебаний ЭМВ в 1 с, а порция энергии в одной моде (на длине l0) Эм1 = Э0 /N0 = Э0/ n = Э0×Т, где Т – период одного полного колебания в ЭМВ.
2. Условия отражения на границах полости определяют существование там только узлов волн. Допуская, что сравнительно со скоростью ЭМВ поршень перемещается ничтожно медленно, приходим к выводу о том, что вследствие сохранения местоположения узлов волн на границах полное число мод вдоль полости, между ее торцом и торцом поршня сохраняется:
N = N0 = C/l0 = n0 = 
= 
= сonst. (2.1)
3. Следствием идеальной подгонки поршня к полости и отражательных способностей границ является отсутствие потерь излучения из объема полости, а следовательно – сохранение неизменным количества энергии излучения в полости, несмотря на изменение ее размеров
Э = Э0 = const. (2.2)
Отсюда следует, что при адиабатных условиях изменения размеров полости сохраняется неизменной энергия, приходящаяся на одну моду МПП ЭМВ:
Эм = Э0/N0 = Э0/n0 = const. (2.3)
Вследствие произвольности исходных предположений полученные выводы верны для МПП ЭМВ произвольной длины и для полостей любых размеров.
4. Считая, что в однородной среде физического вакуума скорость ЭМВ не изменяется (С = const), не зависит от перемещения поршня и размеров полости, для времени t однократного прохождения длины х полости излучением запишем:
t = х/C = x/(ln)
= T = N0T = N T;
(2.4)
откуда
(t/T) = n = (x/l) = N0 = const, (2.4, а)
так как число мод в полости остается одинаковым N = N0 = n0
5. Мощность излучения Р, приходящаяся на единицу площади 1м2 поперечного сечения полости в единицу времени 1с
Р = 
= 
= 
= 
= 
= 
l0, (2.5)
изменяется обратно пропорционально размеру полости.
Значения объемной плотности энергии излучения также варьируются в зависимости от размера полости:
U = 
= 
= 
(при S0 = 1м2 ).
(2.5,а)
Энергия одной моды МПП ЭМВ в условиях адиабатического изменения размеров полости сохраняется неизменной в результате соответственного изменения длины отдельной моды:
l0 = х0/n0;
l = х/n0 = l0 
(при n = const), (2.6)
так как 
= 
= n0 = const.
6. В связи с тем, что число мод в полости, изменяющей свои размеры в адиабатных условиях, остается одинаковым, то эквивалентно изменяется частота излучения
n = n0 
= n0 
, (2.7)
что отвечает неизменности скорости ЭМВ в вакууме: С=n l = n0× l0=const.
Из полученных результатов следует:
- постоянство количества энергии, соответствующей одной моде МПП ЭМВ, независимо от пути и способа ее образования и частоты (длины волны) исходного излучения;
- процесс адиабатного преобразования любой исходной частоты ЭМВ (в опытах при изменении объема полости с идеально отражающими стенками) в иную другую частоту доказывает сохранение энергии, приходящейся на отдельную моду, хотя и изменяющуюся по всей длине волны и частоте;
- любая МПП ЭМВ имеет в любой моде произвольной частоты одно
количество энергии Эм [
= Дж с]:
Эм = 
=
const;
- по современным представлениям за квант энергии излучения принята энергия, которой обладает число мод ЭМВ, равное частоте n (числу полных колебаний в 1с):
Э0n = hn,
где h = 6,626176 ×10 -34 Дж с – постоянная Планка;
- энергия одной моды излучения (по крайней мере, в условиях термодинамического равновесия) – это эквивалент постоянной Планка М:
=
Эм º h.. (2.8)
- не исключена возможность нарушения соотношения (2.8) вне условий термодинамического равновесия; например, при люминесценции.
7. Хаотическое тепловое механическое движение микрочастиц приводит к статистическому закону Больцмана – Максвелла распределения энергии по уровням. Например, распределение давления в атмосфере планеты эквивалентно распределению плотности энергии по высоте, т. к. размерности одинаковы
[Р] = Па = 
º 
= 
= [
= rэ]. (2.9)
Если на высоте Z в атмосферу ввести порцию энергии (определенное количество частиц с этой энергией) e0z , то она распределяется по высоте атмосферы по закону Больцмана – Максвелла. Оставляемая на высоте Z часть порции этой энергии равна:
Э1Z = Э0Z е
= Э0Z е
, (2.10)
где b = 
– показатель степени, m – масса частицы; g –
ускорение свободного падения; mgZ = Э0Z –
энергия на уровне Z атмосферы; k – постоянная Л. Больцмана; Т –
абсолютная температура; kT – среднестатистическая энергия
теплового движения микрочастиц атмосферы.
Очевидно, что эта оставшаяся порция избыточна. Она под действием теплового хаотического движения подвергается перераспределению и уже от нее снова в этот слой отделяется вторая доля энергии по закону Больцмана – Максвелла:
Э2Z = Э1Z е = Э0Z е
. (2.11)
Для произвольной i-й доли энергии в i-м акте перераспределения имеем:
Эiz = Э0Z е
. (2.12)
В конечном итоге на указанный слой с высотой Z отделяется результирующая доля исходной энергии:
= 
= 
= 
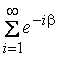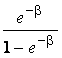(2.13)
8. Энергия, которой обладают микрочастицы (химически стабильные) вещества, в общем случае слагается из механической энергии хаотического движения и энергии излучения. Кроме "хаотического" теплового механического движения любая микрочастица находится в колебательном движении вся в целом или ее отдельные составляющие, что обеспечивает им поддержание энергетического баланса с внешним электромагнитным полем (ЭМП). Каждая микрочастица должна получать и отдавать ЭМП в единицу времени столько и такого качества энергии излучения, сколько и какого качества она получает, т. е. на частоте n – порцию энергии Э0n на одну моду стоячей ЭМВ (электромагнитной волны), образующейся в условиях ТДР (термодинамического равновесия).
Однако порция энергии e0n на частоте n, излучаемая во вне микрочастицей, попадает в систему большого числа микрочастиц, находящихся в ТДР и совершающих бесконечное множество перераспределений по закону Больцмана – Максвелла, что по аналогии с порцией энергии механического движения (2.13) приводит к результирующей доле энергии излучения, отделенной статистическим усреднением характеристик в ходе хаотического теплового движения частиц вещества:
Эрез n = Э0n 
(2.14)
Таким образом, согласно (2.14), порция энергии излучения отдельной микрочастицы, попав в систему бесконечного множества других частиц, в условиях ТДР после многих перераспределений по энергетическим уровням, согласно статистическому закону распределения Больцмана – Максвелла, вырождается в результирующую порцию энергии излучения этого множества частиц вещества.
В итоге а) для вывода формулы плотности спектрального излучения черного тела М. Планку в 1900 г. совсем не требовалось представление о квантовой природе света (ЭМВ);
б) соотношение (2.14) (и его аналог (2.13)) между отдельной порцией энергии и результирующей порцией, оставляемой на этой частоте излучения бесконечными перераспределениями в системе ТДР, является следствием действия закона Больцмана – Максвелла распределения по энергетическим уровням при Т = (X,Y,Z,t) = const;
в) возможность приложения закона Больцмана – Максвелла к ЭМП при Т(X,Y,Z,t) = const в условиях ТДР следует из общеизвестного закона сохранения энергии;
г) с учетом вышеизложенного соотношение (2.8) легко приводится к виду известной формулы М. Планка, что наглядно показано в работе автора [1] для случая равновесного излучения газа в полости на базе теоретически и экспериментально обоснованного закона смещения излучения В. Вина.
Следует отметить, что h – постоянная Планка для энергии
моды равновесного излучения не должна вызывать недопонимания
у тех исследователей, для которых k – постоянная Л.
Больцмана является характеристикой энергетического уровня отдельной
молекулы идеального газа вещества. Эти две характеристики подобны
друг другу, только h относится к полю излучения, а k –
к веществу и, пожалуй, только в условиях термодинамического
равновесия. Мы не учитываем дискретность энергии Эч частицы
вещества, т.к. принимаем бесконечно плавное изменение температуры Т:
Эч = kТ. Аналогично, нельзя утверждать
дискретность энергии Эл моды излучения, полагая
бесконечно плавное изменение частоты: Эл =h
.
В природе существует дискретность строения частиц вещества,
обусловленная их взаимным энергообменом. От дискретности внутреннего
строения частиц вещества происходит дискретность спектров их
излучения, т.е. дискретность частоты 
, на которой ПРИРОДОЙ «разрешено» им излучать и поглощать
энергию.
Из последнего следует, что должно быть и обратное явление для вещества – существуют дискретные уровни температур как уровни излучения для микрочастиц вещества, разрешенные ПРИРОДОЙ для их жизнедеятельности. Это означает, что если энергия излучения изменяется дискретно, скачками, порциями, то и температура должна иметь аналогичные свойства.
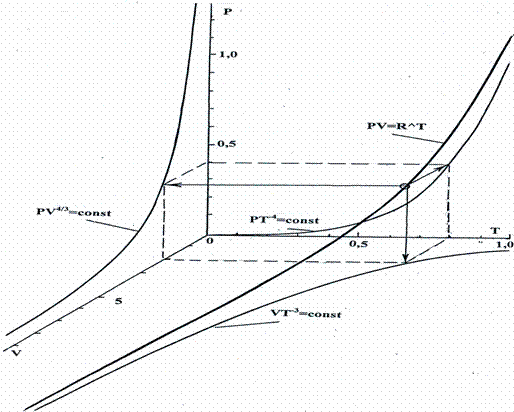
На пути развития этой аналогии автору удалось получить уравнение состояния поля излучения, которое по форме математической записи сходно с уравнением Клапейрона – Менделеева для состояния идеального газа: PV = RлT, где Rл= 5,131*10-9 Дж К-1 м-3 (универсальная постоянная поля излучения)[2].
Существенное отличие графического изображения этого уравнения от графика уравнения состояния идеального газа состоит в том, что с увеличением температуры объем поля излучения уменьшается, а объем идеального газа вещества увеличивается[3; С. 38].
Диаграмма состояния интегрального поля равновесного теплового излучения приведена на рисунке 1.
|
|
| Рис. 1. Диаграмма состояния интегрального поля равновесного теплового излучения |
III. Между закономерностями распространения звуковых волн (ЗВ) в среде некоторого вещества и электромагнитных волн (ЭМВ) в вакууме выявляются следующие аналогии, вскрывающие взаимосвязи различных полей:
1. Закон Ома
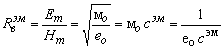, (3.1)
, (3.2)
где для ЭМВ: 
– амплитуды векторов напряженностей электрического
и магнитного полей; 
магнитная и электрическая постоянные вакуума; 
–
скорость света; 
– волновое сопротивление вакуума;
для ЗВ: 
– амплитуда векторов давления и скорости
смещения частиц среды; 
– плотность вещества среды и адиабатическая объемная
сжимаемость среды; 
– скорость звука ; 
– волновое сопротивление среды для звука
;
2. Скорость ЭМВ
в вакууме
; (3.3)
в среде 
, (3.4)
где 
– относительные магнитная и диэлектрическая проницаемости
ЗВ в среде
.
(3.5)
3. Волновое сопротивление
ЭМВ, вакуум 
;
(3.6)
3В, вещество 
. (3.7)
Построенная аналогия проявляет физический смысл характеристик среды вещества и поля вакуума:
плотность вещества
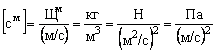, (3.8)
где 
– механический Ом;
электромагнитная плотность вакуума
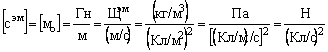; (3.9)
сжимаемость вещества среды (адиабатическая)
; (3.10)
электрическая сжимаемость вакуума
. (3.11)
Например, плотность вещества соответствует механическому давлению, необходимому для создания (а не поддержания) единичной скорости смещения микрочастиц среды, ЗВ, или соответствует силе, связанной с единичной скоростью перемещения в пространстве. Согласно анализу размерностей, следует характеризовать относительную сжимаемость поля вакуума величиной
.
Сжимаемость 
соответствует относительному
изменению объема среды, приходящегося на единицу давления в
адиабатических условиях.
Электрическая сжимаемость вакуума 
– это изменение квадрата некоторой
поверхностной плотности электрозарядов, приходящееся на единицу
давления, или пространственного взаимоградиента электрозарядов
– на единицу силы их взаимодействия.
Электромагнитная плотность вакуума соответствует силе, связанной с единичной скоростью переноса электрозарядов.
Необходимо отметить, что приведенные примеры не исчерпывают всех толкований физического смысла рассмотренных величин.
Из анализа взаимодействия электрических, магнитных и гравитационных полей следуют эквиваленты:
1 – статическая гравитационная постоянная вакуума
,
(3.12)
характеризующая пространственный гравитационный градиент, соответствующий единице силы;
2 – cтатический электрогравитационный эквивалент массы вещества и электрического заряда
.
(3.13)
3 – динамический электрогравитационный эквивалент
(3.14)
4 – статический магнитногравитационный эквивалент
. (3.15)
5 – динамический магнитногравитационный эквивалент
. (3.16)
6 – динамический электромагнитный эквивалент – скорость света
(
) . (3.17)
7 – статический электромагнитный эквивалент – волновое сопротивление вакуума
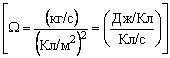. (3.18)
8 – динамическая гравитационная постоянная вакуума
, (3.19)
характеризующая силу взаимодействия движущихся масс.
Статические силы взаимодействия пропорциональны произведению погонных плотностей масс вещества в законе тяготения Ньютона или электрозарядов.
Анализ выражений для статических законов тяготения Ньютона и взаимодействия электрозарядов Кулона позволил выявить следующее: статическая сила взаимодействия прямо пропорциональна произведению погонных плотностей масс или электрозарядов, отнесенных к единице длины расстояния r между телами (это пространственный градиент взаимодействующих масс и электрозарядов):
тяготение масс 
; 
; 
;
электрозарядов : 
; 
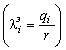. (3.20)
5. Динамическое взаимодействие движущихся со скоростью 
тел с массами 
или электрозарядами 
характеризуется выражениями
; 
(3.21)
; 
.
В результате взаимосвязи статических и динамических постоянных вакуума электрического и гравитационного полей получаем
; 
(3.22)
где 
– критерий Маха, световой.
Условие (3.22) позволяет получить для результирующей силы, равной разности статических и динамических сил, следующие выражения:
; 
. (3.23)
Заметим, что последним нашим результатам аналогична взаимосвязь
давления 
, действующего на боковую поверхность трубки течения,
и полного давления 
в потоке вещества
,
(3.24)
где 
– критерий Маха (механический) скорости для движущегося
вещества среды; 
–
максимальная скорость среды при данном полном давлении
– динамический напор, равный давлению движущейся
среды при скорости 
относительно измерителя давления.
Общая подмеченная закономерность уменьшения силы взаимодействия тел через электрические, магнитные, гравитационные поля представляется в виде квадратичной зависимости от скорости движения тел, носителей (источников) этих полей.
Мощность плотности потока энергии, переносимой волной
ЭМВ 
ЗВ 
, (3.25)
где 
– напряженность магнитного поля как скорость пространственного
градиента электрозаряда; 
– скорость смещения частиц среды в волне.
6. Скорость звука в чистых металлах убывает с увеличением
веса А и межатомного расстояния d в кристаллической
решетке 
. (3.26)
Скорость ЭМВ (света) в оптических кристаллах также проявляет
тенденцию к уменьшению с ростом атомных весов ионов 
и
межатомных расстояний в кристаллической решетке 
:
, (3.27)
где х, y – показатели степени, определяемые из опытных данных для конкретных кристаллов.
7. Движение источника в среде со скоростью,
большей скорости звука 
или соответственно скорости света 
,
вызывает конус Маха – результирующую волну с единым коническим
фронтом, угол раскрытия 
которого
определяется одинаково
а) в механике – сверхзвуковое движение 
;
б) в оптике – эффект Черенкова – Вавилова 
;
(3.28)
где М =
– число Маха для ЗВ и ЭМВ; n – показатель преломления; 
– скорость света в вакууме.
При этом интенсивность черенковского свечения почти не зависит
от химического состава среды, а в интервале волновых чисел 
(
– длина волны излучения) на пути
в 1 см зависит от электрозаряда 
микрочастицы и угла конуса Маха 
:
(3.29)
8. Если в одной среде одновременно в одном направлении распространяются
ЗВ и ЭМВ, то их взаимодействие будет характеризоваться отношением
волновых сопротивлений для 3В и для
ЭМВ:
.
Полученный результат интересен тем, что его размерность равна квадрату поверхностной плотности электрозарядов. Поэтому следует ожидать, что в среде при параллельном движении по одной траектории ЗВ и ЭМВ (бегущих или стоячих) будут возникать дополнительные электрозаряды и эквивалентные им электрополя, а характеристики этих полей способны раскрывать свойства среды, ЗВ и ЭМВ. При этом особенные эффекты можно ожидать при совпадении и кратности частот ЗВ и ЭМВ с собственными частотами систем тел и сред.
9. Отметим результаты, полученные при решении несколько необычной
стационарной задачи: плоский конденсатор заряжен электрозарядами
с поверхностной плотностью 
; между обкладками – вакуум; от независимых
источников электроэнергии вдоль обкладок пропускаются равные
встречные токи; для плоской системы пластин – обкладок в вакуумном
зазоре.
Имеем следующие характеристики электрического и магнитного полей:
; 
;
; 
, (3.30)
где Н, Е – напряженности магнитного и электрического
полей; В, D – индукции этих полей; 
– погонная плотность электротока на единицу длины вдоль
оси Z, а сам ток течет вдоль оси X; 
– поверхностная плотность электрозарядов на обкладках
на единицу площади; 
–напряженность электрического поля в зазоре вдоль оси
Y; 
–напряженность магнитного поля в зазоре вдоль оси Z,
которую можно выразить через поверхностную плотность электрозарядов
и скорость их движения 
вдоль оси Х (
, 
)
:
. (3.31)
Условие равновесия сил, действующих со стороны электрического и магнитного полей на обкладки, имеет вид
(3.32)
или
. (3.32,а)
Из последнего соотношения следует
, (3.33)
что скорость движения электрозарядов тока в пластинах точно
равна скорости света! В стационарных условиях это можно выразить
так: 
; 
Далее из этого условия для напряженности электрополя в зазоре имеем
,
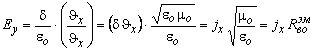(3.34)
где волновое сопротивление вакуума будет равно:
. (3.35)
Это закон Ома для стационарных электрического и магнитного полей (в дифференциальной форме), связывающий напряженность электрического поля в вакууме зазора между обкладками с линейной погонной (на единицу длины вдоль оси Z) плотностью электротока, направленного вдоль оси X (по длине обкладки), и с волновым сопротивлением вакуума. Это само по себе вызывает интерес, т.к. было получено и нашло применение волновое сопротивление только в переменных электрических и магнитных полях.
10. Если по условиям предыдущей задачи зазор конденсатора
будет заполнен некоторым веществом с относительными диэлектрической 
и
магнитной 
проницаемостями,
то соответствующие выражения преобразуются следующим образом:
; 
, (3.36)
; 
. (3.37)
Точные выражения для скорости электромагнитной волны и волнового сопротивления также получены для стационарных условий, в которых никаких волновых процессов не наблюдается.
Из найденных решений следует необычный вывод: стационарный постоянный ток встречает сопротивление, зависящее от магнитных и диэлектрических свойств окружающей среды, в том числе вакуума; это сопротивление повышается с ростом относительной магнитной проницаемости и уменьшается с увеличением относительной диэлектрической проницаемости; скорость движения электрических зарядов в проводнике зависит только от свойств наружной среды. Ее значение уменьшается с увеличением значений относительных магнитной и диэлектрической проницаемостей.
Однако свойства самого проводника обкладок не играют роли в условиях данной стационарной задачи. Значит ли это, что электрозаряды текут вне структуры проводников, а обычное активное сопротивление электротоку уменьшается благодаря стационарному полю?
Возможно, результат взаимодействия электрических зарядов, протекающих через электрическое поле, и электротоков – через магнитное поле, зависит только от свойств внешнего вакуума, среды и относительного движения зарядов в электротоке.
Следует обратить внимание на то, что полученные результаты приведены без привлечения аппарата анализа нестационарных и колебательных волновых процессов.
Безусловно, теоретические положения объясняют результаты, полученные Г.В. Николаевым в ходе экспериментов, например, по влиянию постоянного магнитного поля на размер катодного темного пространства тлеющего разряда [ 9; С. 48 ].
Выводы о движении энергии электротока за пределами металлического
проводника в наружном пространстве, вакууме и диэлектрической
среде, полученные для стационарных условий, подтверждаются
результатами работ по высоко экономичному способу передачи
электроэнергии посредством реактивных составляющих 
.
Общие выводы. Полученные результаты дополняют и углубляют известные данные об аналогии электрических, магнитных, гравитационных и механических явлений, как стационарных, так и динамических; выявлена общность квадратичной зависимости от скорости движения в рассмотренных явлениях; установлены некоторые новые эквиваленты взаимосвязей разных по природе физических явлений. В результате исследований выведен закон Ома для стационарных электрического и магнитного полей в дифференциальной форме, включающий волновое сопротивление вакуума. Без представлений о квантовости (непланковским подходом) выведен закон спектрального излучения черного тела.
Впервые приведены уравнение и диаграмма состояния поля излучения.
Список литературы
1. Агеев Ю.М. К теории равновесного излучения // Труды Международного конгресса 2000 г. «Фундаментальные проблемы естествознания и техники». Спб., 2000.Т. 1, № 1. С. 15–17.
2. Агеев Ю.М. К теории равновесного излучения // Труды Международного конгресса 2002 г. «Фундаментальные проблемы естествознания и техники». Спб., 2002. Ч. 1 С. 7–11.
3. Шепф Х.Г. От Кирхгофа до Планка. М.,1981. 192 с.
4. Черняев А.Ф. Русская механика. М., 2001. 592 с.
5. Бергман Л. Ультразвук и его применение в науке и технике. М.,1957. 727 с.
6. Калашников А.М. Основы радиотехники и радиолокации/ А.М. Калашников, Я.В. Степук. М., 1962. 366 с.
7. Физические величины: Справочник. М.,1991. 1232 с.
8. Физика: Большой энциклопедический словарь. М., 1998. 944 с.
9. Николаев Г.В. Непротиворечивая электродинамика. Теории, эксперименты. Парадоксы. Томск, 1997. 144 с.
10. Стребков Д.С. Возможность передачи электрической энергии без металлических проводов // Докл. РАСХН, 2002. №1. С.47–50.
Научный электронный журнал КубГАУ . № 02(2), 2003