Научный электронный журнал КубГАУ . № 02(2), 2003

ЭКСПЕРИМЕНТАЛЬНАЯ ФАКТОРНАЯ МОДЕЛЬ ПРОЦЕССА АКУСТО-МАГНИТНОЙ ОБРАБОТКИ ТОПЛИВА

Коржаков Алексей Валерьевич - соискатель, ст. преподаватель

Адыгейский государственный университет

Лойко Валерий Иванович - д.т.н., профессор

Кубанский государственный аграрный университет

Всевозрастающее воздействие человека на природу привело к возникновению экологических проблем в экосистеме биосферы, в частности, проблемы загрязнения атмосферы выхлопными газами автотранспорта. Для решения этой задачи предлагается использование новых методов очистки отработанных газов от вредных примесей за счет обеспечения более полного сгорания топлива двигателей автотранспорта.

Одним из методов снижения вредных выбросов в атмосферу является предварительная обработка топлива автомобильных двигателей в акустических и электромагнитных полях.

Этот метод был применен в акусто-магнитном аппарате (АМА), который устанавливается в систему питания двигателей внутреннего сгорания с целью повышения эффективности сгорания топлива. Более полное сгорание топлива приводит к снижению содержания вредных примесей в отработанных газах, что, в свою очередь, способствует улучшению экологической обстановки.

АМА обеспечивает более полное сгорание топливно-воздушной смеси путем предварительной обработки углеводородной молекулы топлива в акусто-магнитном поле, которое работает в резонансном режиме, без изменения конструкции двигателя.

В основе разработки лежит диспергирование за счет эффекта омагничивания, осуществляемое на основе закона физики о ядерномагнитном резонансе (увеличение энергоемкости атомов при направленном воздействии магнитного поля), магнитострикции и флокуляции (организация и объединение коллоидных частиц в хлопьевидные агрегаты (коагуляция)).

Предварительные исследования экологической эффективности данного метода в лабораторных и реальных условиях показали, что в отработанных газах резко снижается содержание тяжелых металлов и углерода. В результате проведения прямых многократных измерений были получены и обработаны величины расхода топлива за единицу пройденного пути, а также экологические показания СО и СН.

Измерение расхода топлива проходило в абсолютно одинаковых условиях: на одном и том же отрезке дороги, в одном направлении движения, в одно время суток. Сначала проводили серию опытов на автомобиле с карбюраторным двигателем без АМА. Следующая серия опытов была осуществлена после установки на автомобиль АМА. Всего проведены три серии опытов, каждая из которых состояла из восьми опытов. Полученные результаты сведены в таблицу.

Таблица - Результаты измерения расхода топлива

На основе проведен ных экспериментов непосредственно на самом техническом объекте (автомобиле) была построена э кспериментальная факторная модель, так как сложность системы и условия функционирования не позволяют надеяться на требуемую точность их математического описания теоретическими методами.

При построении экспериментальной факторной модели объект моделирования представляется в виде "черного ящика", на вход которого подаются  пере­менные (частота входного сигнала, зазор рабочей области) и (рабочие условия),  а на выходе можно   наблюдать   и   регистрировать    переменные (расход топлива за единицу пройденного пути, экологические показания СО и СН). В число входных переменных и входят внутренние и внешние параметры объекта проектирования, подлежащие оптимизации, а выходными переменными "черного ящика" являются выходные параметры объекта, характеризующие его эффективность и качество процессов функционирования, выбираемые в качестве критериев оптимальности. [1, C. 464]

В процессе проведения эксперимента изменение переменных и  приводит к изменениям выходных переменных . Для построения факторной модели регистрировались эти изменения и осуществлялась необходимая их статистическая обработка для определения параметров модели.

Общепринято, что в вычислительных экспериментах объектом исследования является теоретическая математическая модель, на основе которой необходимо получить экспериментальную факторную модель. Для ее получения необходимо определить структуру и чис­ленные значения параметров модели.

Структуру модели  выбираем на основе априорной информации об объекте с учетом назначения и последующего использования модели. Задача определения параметров модели полностью формализована. Она решается методами регрессионного анализа. Регрессионную модель можно представить выражением

,

где  — вектор параметров факторной модели.

Вид вектор-функции  определяется выбранной структурой модели и при выполнении регрессионного анализа считается заданным, а параметры B подлежат определению на основе результатов эксперимента, проводимого в условиях действия поме­хи , представляемой в виде аддитивной составляющей функции отклика . [1, C. 466]

Для получения адекватной математической модели необходимо обеспечить выполнение определенных условий проведения эксперимента. При проведении активного эксперимента задается определенный план варьирования факторов, т. е. эксперимент заранее планируется.

В активном эксперименте факторы могут принимать только фиксированные значения. Минимальный Х _min и максимальный – Х _max, уровни всех факторов выделяем в факторное пространство, некоторый гиперпараллелепипед, представляющий собой область планирования. В области планирования находятся все возможные значения фак­торов, используемые в эксперименте.

Вектор  задает точку центра области планирования. Координаты этой точки  выбираем из соотношения:

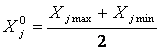
Точку   определяет основной уровень факторов . Интервал  варьирования фактора X_j, вычисляем по формуле   

                                      DX_j = (X_{j max} – X_{j min})                                                

Факторы нормируем, а их уровни кодируем. В кодированном виде верхний уровень обозначают +1, нижний -1, а основной 0. Нормирование факторов осуществляют на основе соотношения

                                 .                            

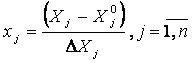Для переменных  начало координат совмещено с центром эксперимента, а в качестве единиц измерения используем интервалы варьирования факторов. Геометрическое представление области планирования  показано на рис. 1. Центр эксперимента находится в точке 0 с координатами . Точки 1,2,3,4 являются  точками плана   эксперимента. План эксперимента удобно представлять в матричной форме. [1. C. 471]

Матрица спектра плана имеет вид:

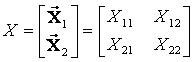
Опыты при выполнении эксперимента проводились в последовательности, предусмотренной матрицей плана.

Параметры факторной математической модели определяем методами регрессионного анализа.

Для определения параметров используются результаты эксперимента. Результаты эксперимента можно представить функцией вида,

где   — аддитивная помеха случайного характера с нормальным законом распределения. В качестве базисных функций используем переменные простейших полиномов: у = b₀ + b₁х₁ + b₂х₂ , параметры модели b_0,b₁,b₂ находим путем решения системы нормальных уравнений.

Используя данные табл. 1, получим систему нормальных уравнений. Решая систему уравнений, получим модель:

                                         y=7,855-0,0043X₁-0,02X₂

Для определения тесноты связи предварительно вычисляем парные коэффициенты корреляции  ,,.

=0,00; =-0,42=-0,91.

После этого вычисляем коэффициент множественной корреляции =1,00

Таким образом, степень тесноты связей является очень высокой.

Для оценки адекватности и точности построенной модели сформируем остаточную последовательность, для чего из фактических значений уровней ряда вычтем соответствующие значения по модели. Проверку случайности уровней ряда проведем на основе критерия пиков. Количество точек пиков равно единице, т.е. неравенство 1>0 выполняется. Следовательно, можно сделать вывод, что свойство случайности ряда остатков подтверждается.

Результаты предыдущей проверки дают возможность провести проверку соответствия остаточной последовательности нормальному закону распределения. Воспользуемся RS-критерием: RS=1,64 , и это значение попадает в интервал между нижней и верхней границами табличных значений данного критерия.

Проверка равенства нулю математического ожидания ряда остатков подтверждается (-0,02) не прибегая к статистике Стьюдента.

Для проверки независимости уровней ряда остатков (отсутствия автокорреляции) вычислили значение критерия Дарбина-Уотсона. Расчеты дают следующее значение этого критерия: d=1,18. Данное значение сравниваем с двумя критическими значениями критерия, которые для линейной модели в нашем случае можно принять равными d₁=1,08 и d₂=1,36. Так как расчетное значение попадает в интервал от d₂ до 2, то делаем вывод о независимости уровней остаточной последовательности.

 Из сказанного выше следует, что остаточная последовательность удовлетворяет всем свойствам случайной компоненты временного ряда, следовательно, построенная линейная модель является адекватной.

Для характеристики точности модели воспользуемся показателем средней относительной ошибки аппроксимации, который равен: 0,253(%). Полученное значение средней относительной ошибки говорит о достаточно высоком уровне точности построенной модели.

                                                          ЛИТЕРАТУРА

1. Тарасик В.П. Математическое моделирование технических систем / В.П. Тарасик.- Мн.: ДизайнПРО, 1997.

Научный электронный журнал КубГАУ . № 02(2), 2003