Научный электронный журнал КубГАУ . № 02(2), 2003
УДК 539.3:534:532.5
Нелинейные уединенные ударно-волновые структуры в вязкоупругих стержнях
Аршинов Г.А. – канд. физ.-мат. наук, доцент
Кубанский государственный аграрный университет
Лаптев В.Н. – канд. техн. наук, доцент
Кубанский государственный аграрный университет
Елисеев Н.И. – аспирант
Краснодарский военный институт им. С.М. Штеменко
Предложен вывод уравнений движения геометрически нелинейного вязкоупругого стержня с учетом инерции поперечных движений и использования неклассических кинематических уравнений. Проанализирован общий случай, когда вязкоупругие свойства проявляются при объемных и сдвиговых деформациях. Для эволюционного уравнения Кортевега де Вриза – Бюргерса, к которому сводятся методом возмущений полученные уравнения движения, определено точное решение, описывающее продольные уединенные волны. Определены условия формирования ударно-волновых структур деформации сжатия и растяжения стержня.
В работе [1] исследуются уединенные нелинейные волны в упругих стержнях. Дисперсионные нелинейные волны в вязкоупругих стержнях при упругих объемных деформациях рассмотрены в монографии [2]. В отличие от [2] в предлагаемой cтатье проанализирован более общий случай распространения уединенных волн, когда вязкоупругие свойства стержня проявляются при объемных и сдвиговых деформациях.
Рассмотрим бесконечный
стержень неизменного поперечного сечения, свободный от внешних объемных и
поверхностных воздействий. Введем систему координат, направив ось 
вдоль линии центров тяжести поперечных сечений, а оси 
и 
расположим в одном из них. Учитывая
инерцию поперечных движений, аппроксимируем перемещения точек стержня функциями
[1]
, (1)
где 
– соответственно перемещения по осям x, y, z, 
– время, 
- коэффициент Пуассона.
Конечные деформации стержня зададим соотношениями тензора Грина:
(2)
предполагая, что 
, 
Воспользуемся уравнениями линейной вязкоупругости для описания наследственных реологических свойств стержня 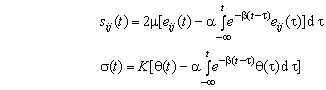[3]
, (3)
где 
- соответственно компоненты девиаторов напряжений и
деформаций; 
−
среднее напряжение, 
- объемное расширение, 
− модуль объемной
деформации, 
- параметр Ламе; 
- константы, определяющие
реологические свойства стержня; Е - модуль Юнга;
- коэффициент Пуассона.
С целью упрощения
исследования интегральные операторы в уравнениях (3) заменим дифференциальным
разложением функции 
в ряд Тейлора по степеням (
), ограничиваясь при этом
двумя слагаемыми, при условии 
>>1.
В результате получаем приближенные формулы для компонент напряжений
, (4)
где введен оператор L, определяемый равенством 
и действующий на функцию 
по правилу 
, а 
− параметр Ламе.
Формулы (4) представим в развернутом виде:
;
;
;
или
;
;
;
,
где
, 
, 
,
, 
, 
.
Уравнение движения стержня получим из вариационного принципа
, (5)
где точкой обозначена производная по t, r - плотность материала стержня, 
- вариации деформаций, 
– вариации перемещений, а
тройной интеграл вычисляется по объему стержня.
Вычислим вариации деформаций стержня
,
,
,
.
Определим вариацию внутренней энергии стержня, используя формулы (4), а также вариации компонент деформации
+
+
+
.
После преобразований приходим к равенству:
+
.
Уравнение движения стержня получим из (5) после подстановки в него значения вариации внутренней энергии:
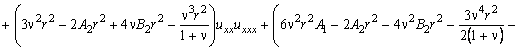
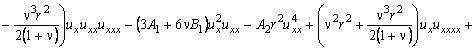
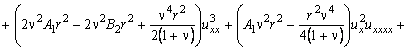
.После преобразования уравнение представим в виде:
.
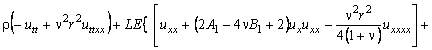
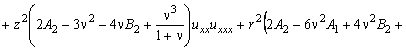
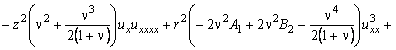
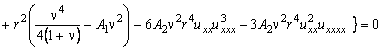В последнем уравнении движения перейдем к безразмерным переменным
, 
, 
, 
, 
,
где 
– амплитудный параметр возмущения; 
, d
– соответственно характерные длина волны и поперечный размер стержня, 
скорость волны, 
– характеристика
нелинейности волнового процесса.
Допустим, что – малый параметр, т.е.
характерная длина волны значительно
превосходит амплитудный параметр , а поперечный размер стержня и
реологические постоянные 
определяют отношения порядков
, 
.
Пренебрегая членами порядка выше, чем 
, получаем безразмерное уравнение движения стержня:
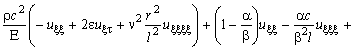
(6)
Для анализа уравнения (6)
применим метод возмущений. Представим функцию 
в виде асимптотического разложения
. (7)
Осуществим подстановку асимптотического разложения (7) в уравнение (6), и с учетом введенных соотношений порядков в нулевом приближении получим
.
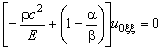Согласно условию 
, из последнего уравнения найдем скорость распространения
продольной волны в линейно-вязкоупругом стержне
. (8)
Из формулы (8) при 
, т.е. отсутствии свойства
вязкости, вытекает известная формула для скорости распространения продольной
волны в линейно-упругом стержне:
.
Для разрешимости
уравнения относительно неизвестной функции 
в разложении (7), полученном из первого приближения,
необходимо, чтобы u
удовлетворяло известному уравнению
Кортевега де Вриза – Бюргерса:
, (9)
где 
, 
, 
.
При исследовании
продольных волн в линейно-вязкоупругих стержнях были введены малый параметр 
и отношение порядков 
из которого следует 
~ d2.. Таким образом, для возникновения уединенной волны в
стержне требуется условие, связывающее характерный линейный размер стержня,
амплитуду и длину волны.
В работе [4] представлено подробное описание точного решения этого уравнения (9):
, (10)
где
, 
или
,
где
, 
.
Используя следующие обозначения
, 
, 
,
получим выражение:
.
При 
запишем неравенства вида 
, 
и найдем коэффициенты с1,
с2, с3:
, 
; 
, 
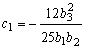имеет знак 
,
, 
.
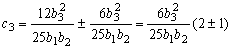Если в уравнениях выбран
верхний знак “+”, то с учетом 
и 
уравнение примет вид:
где
.
Согласно условию 
, получим 
,
где
, а 
.
При 
.
Производную представим следующим выражением:
.
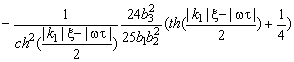Из уравнения 
найдем критические точки
функции. В ходе преобразований получаем: 
. Функция 
будет максимальна в точке, определенной значением
, являющимся
корнем уравнения:
.
Тогда максимальное значение функции найдем по формуле
,
которую можно записать в виде
.
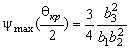Вышеприведенный анализ
показывает, что при ранее указанных условиях решение уравнения (9) будет иметь
структуру ударной волны, т.е. в линейно-вязкоупругом стержне образуется ударная
волна растяжения 
.
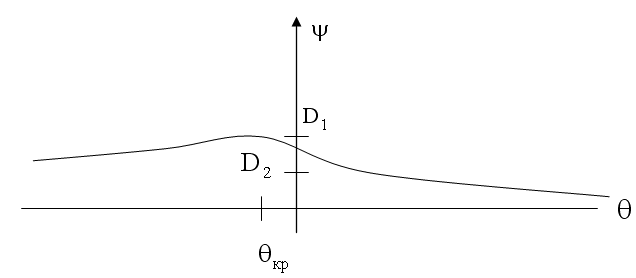
На рисунке представлена зависимость деформации от перемещения и введены обoзначения:
Возвращаясь к размерным переменным
),
определим поправку к скорости распространения волны, согласно выражению:
.
Список литературы
1. Потапов А.И. Нелинейные волны деформации в стержнях и пластинах. Горький: Изд-во Горьк. гос. ун-та, 1985.
2. Аршинов Г.А., Могилевич Л.И. Статические и динамические задачи вязкоупругости. Саратов: Изд-во СГАУ им. Н.И. Вавилова, 2002, 146 с.
3. Москвитин В.В. Сопротивление вязкоупругих материалов. М.: Наука, 1972.
4. Кудряшов Н.А. Точные решения нелинейных волновых уравнений, встречающихся в механике // Прикладная математика и механика. 1990. Т. 54. Вып. 3. С. 450–453.
Научный электронный журнал КубГАУ . № 02(2), 2003