Научный электронный журнал КубГАУ . № 02(2), 2003

УДК 338.436.33

Функция скорости спроса и анализ оборота

вложенного капитала в интегрированных формированиях АПК

Аршинов В.Г. – соискатель

Кубанский государственный аграрный университет

На основе функции спроса строится математическая модель рентабельной работы интегрированного объединения сельскохозяйственного товаропроизводителя и молокозавода и анализируются параметры увеличения прибыльности перерабатывающего предприятия за счет ускорения оборота вложенного капитала.

В современных рыночных условиях в молочном подкомплексе Саратовской области наблюдается тенденция к объединению сельскохозяйственных товаропроизводителей сырья и перерабатывающих предприятий, выпускающих готовую молочную продукцию, в различные интегрированные формирования. Это связано с тем, что дезинтеграция между этими отраслями особенно негативно отразилась на эффективности сельскохозяйственного производства.

Молокозаводы, находясь в роли монополиста, устанавливают цены на продукцию, основываясь не на рыночном равновесии «спрос – предложение», а на фактических затратах. Это позволяет им без совершенствования производства, улучшения использования ресурсов и повышения конкурентоспособности продукции увеличивать прибыль. В результате наблюдается следующее негативное явление: уровень использования мощностей постоянно снижается и в настоящее время составляет 10–33 %, что связано с сокращением поступления сырья на переработку. Однако, несмотря на ухудшение использования основных фондов и труда, прибыльность многих перерабатывающих предприятий в молочном подкомплексе растет за счет неэквивалентного обмена, т.е. происходит занижение закупочных цен на молоко.

В молочном подкомплексе с целью преодоления кризисной ситуации создаются интеграционные структуры в виде товарищества, акционерного общества, ассоциации, союза, потребительского кооператива, формирования холдингового типа. Для эффективной работы вышеназванных интегрированных формирований необходимо установить параметры, обеспечивающие экономически выгодное сотрудничество всех их участников и позволяющие научно обосновать целесообразность создания и функционирования подобных структур.

С этой целью разработали экономико-математическую модель, определяющую основу и базу для работы интегрируемого объединения, позволяющего участникам интеграционного процесса оперативно реагировать на изменения, происходящие в условиях рынка.

Рассмотрим одну из математических моделей интегрированного формирования сельскохозяйственных товаропроизводителей молока и завода по переработке молочного сырья. В качестве отправной точки возьмем линейную модель функции спроса V(P_з), где Р_з – отпускная цена единицы готовой продукции молокозавода. Обозначим через Р_r рыночную цену единицы готовой молочной продукции, аналогичной поставляемой на рынок заводом.

Предположим, что график функции спроса V(P_з) на продукцию молокозавода (рис. 1) проходит через точки А(Р_r, V_r), В(nP_r, 0), где n>1, V_r – средняя скорость продажи продукции на рынке, сложившаяся к моменту поступления продукции на рынок.

Функция спроса V(P_з) имеет вид:

 . (1)

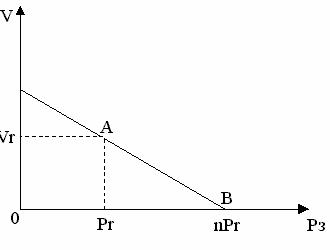
 Рис. 1. График функции спроса V(P_з )

Из условия принадлежности точек А, В графику функции V(P_з) определяем коэффициенты k₁, k₂ из системы:

 . (2)

Выведем решение системы (2):

 , . (3)

Очевидно, что , тогда , а k₁ вычисляется из соотношения (3). Установим выручку, полученную молокозаводом за время реализации готовой продукции t.

 . (4)

Пусть издержки завода по переработке молока  определяются по формуле:

 , (5)

где y – количество переработанного сырья при полной загрузке производственных мощностей завода; С_з – затраты на переработку сырья; Р_t – издержки на покупку единицы сырья.

Прибыль П_з, полученная предприятием по переработке молока, определим из соотношения:

  D (P_з) -С_и

или в развернутой записи, в силу выражений (4),(5), 

 .

Найдем производную  и, приравнивая ее к нулю, получим уравнение для вычисления цены реализации готовой молочной продукции Р_з, обеспечивающей максимальную прибыль перерабатывающему предприятию:

 П_з .

Из этого уравнения найдем цену реализации готовой продукции .

Работа завода по переработке молока будет рентабельной при выполнении следующих неравенств:

 или в развернутой форме:

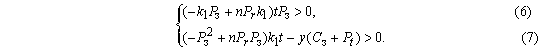 Так как t>0, k₁>0, P_з >0, то приходим к системе неравенств:

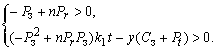
На рисунке 2 изображены области выполнения неравенств (6), (7):

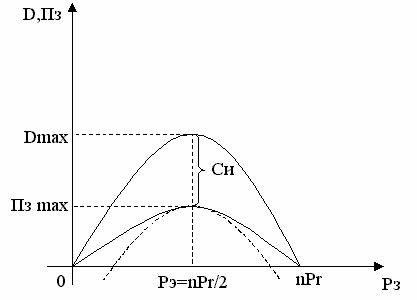
Рис. 2. Область обеспечения рентабельности работы молокозавода: D_max, П_{з max} – максимальные значения выручки и прибыли перерабатывающего предприятия при отпускной цене на готовую продукцию .

Введем коэффициент загрузки производственных мощностей молокозавода α, где . Тогда количество переработанного сырья будет равно α y, а прибыль завода П_з :

 .

Время оборота вложенного капитала Т_об можно найти из уравнения

D (P_з ) = С_и

 или в развернутой записи

,

 отсюда

 . (8)

 Минимум Т_об достигнет в точке .

Если n =2, Р_э=P_r и  при продаже по сложившейся рыночной цене P_r, из формулы (8) находим

.

Коэффициент n задает скорость убывания функции спроса V(P_з) при сложившейся рыночной цене реализации Р_r. Точка В (0, nP_r) определяет нулевую скорость продаж. Вероятно, уже при n = =1,6 скорость будет нулевой, то есть товар не реализуется.

Вычислим отпускную цену реализации готовой молочной продукции Р_э, соответствующую n =1,6:

.

Следовательно, максимальная прибыль будет обеспечена при цене Р_э на 20 % ниже рыночной Р_r; а время оборота T_об будет равно:

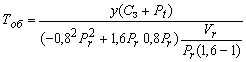
или

,

 то есть на 10 % меньше, чем при Р_з=P_r.

Вычислим П_з(Р_э) и П_з(Р_r):

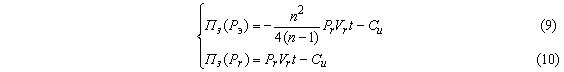 Если n =1,6, то из соотношений (9), (10) имеем:

 , .

Следовательно, П_з(Р_э)>П_з(Р_r) на 7 % при цене реализации готовой молочной продукции  и на 20 % ниже рыночной Р_r.

Таким образом, рассмотренная экономико-математическая модель интегрируемого объединения сельскохозяйственных товаропроизводителей сырья и молокозавода позволила найти научно обоснованные параметры обеспечения рентабельности работы перерабатывающего предприятия, возможность получения достаточно высокой прибыли заводом благодаря не монопольному диктату закупочных цен на сырье у сельскохозяйственных товаропроизводителей, а ускорению процесса товарооборота. Это, несомненно, обеспечит эффективное партнерство всех участников интегрированного формирования. Расчетным путем найдена оптимальная отпускная цена на готовую молочную продукцию завода, которая на 20 % ниже среднерыночной цены на аналогичную продукцию. В этом случае при данной функции спроса V(P_з ) обеспечивается увеличение прибыли на 7 %, а значит, повышение конкурентоспособности продукции завода и снижение ее себестоимости за счет более полной загрузки производственных мощностей предприятия. В итоге налаживается взаимовыгодное сотрудничество перерабатывающего предприятия с сельскохозяйственными товаропроизводителями в рамках интегрированного формирования.

Научный электронный журнал КубГАУ . № 02(2), 2003