Научный электронный журнал КубГАУ . № 01(1), 2003
Обратная граничная задача идентификации фильтрационных потоков к скважине в вариационной постановке
Видовский Л.А., Видовский Л.Л.
Кубанский государственный технологический университет
Кубанский государственный университет
Рассмотрена обратная граничная нестационарная задача (как задача оптимального управления) фильтрации для призабойной зоны скважины и предложен алгоритм ее численного решения. На основании опытных данных о динамике давления на забое восстанавливается кривая изменения притока пластового флюида в скважину после ее остановки. Показана возможность автоматизации процесса сбора и обработки измерений с помощью разработанного авторами автономного измерителя давления и температуры. Внедрение полученных результатов позволит повысить точность математической модели и, в конечном счете, достоверность прогнозирования технологических режимов, назначаемых с помощью этой модели.
На практике наиболее важен выбор режимов эксплуатации скважин, обеспечивающих наибольший их суммарный дебит при наименьших обводненности флюида и содержании песка и минимальные энергетические затраты, что, в конечном итоге, определяет экономическую эффективность разработки.
Параметрами пласта, на основании которых проектируются и осуществляются технологические процессы добычи, составляются схемы и проекты разработки и проводятся анализы разработки месторождений, являются фильтрационные сопротивления (коэффициенты проводимости, подвижности, проницаемости), пьезопроводность, величины и соотношения забойных и пластовых давлений, дебитов. Эти параметры вычисляются в результате обработки информации, получаемой при экспериментальном исследовании скважины. Важнейшим источником такой информации служат кривые восстановления давления (КВД) во время нестационарных режимов ее работы. Остановка или пуск скважины является частным случаем нестационарного режима ее работы.
Большинство методов обработки КВД, построенных с помощью аналитических решений соответствующей краевой задачи, позволяет на основании экспериментально полученной КВД, мощности пласта, коэффициента вязкости флюида и допущений о дебите (притоке пластового флюида в скважину после ее остановки) определить коэффициенты проводимости, подвижности, проницаемости и пьезопроводности, а также пластовое давление и время его восстановления.
В ряде методов мгновенное прекращение фильтрационного притока к скважине вообще не учитывается, а в некоторых , например интегральный метод Г.И. Баренблата и В.А. Максимова [1], приток определяется c большой погрешностью на основе численного дифференцирования или интегрирования экспериментальных данных КВД. В последнем случае необходимо измерять давление на забое, на устье в затрубном (кольцевом) пространстве и на буфере (в подъемных трубах).
Отсутствуют экспериментальные исследования по динамике дебита непосредственно на забое в процессе восстановления давления после остановки скважины. Экспериментально получить динамику полного дебита на забое после остановки скважины технически сложно. С большей точностью можно измерить изменение давления на забое и на основании этой информации численным решением обратной граничной задачи оценить зависимость от времени граничного потока флюида. Термин «оценивание» используется потому, что измерения давления всегда содержат погрешности, влияющие на точность вычисления потока. Более того, если используются точные, но дискретно заданные давления и при этом учитывается конечное число значащих цифр, поток не может быть точно восстановлен.
Обратная граничная задача является по существу задачей оптимального управления и довольно широко применяется в последнее время для идентификации нестационарных тепловых режимов в различных технических приложениях. Известны практические результаты, полученные в ракетной технике, металлургической промышленности и т.д.
Математическая формулировка в одномерной постановке обратной задачи идентификации граничных условий на стенках скважин по экспериментальным данным о КВД следующая.
Требуется определить функции давления ![]() потока на стенке скважин
потока на стенке скважин 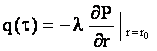 в области
в области ![]() . Начальное распределение давления
и давления на границе влияния скважины, а также фильтрационные характеристики
пьезоповодность
. Начальное распределение давления
и давления на границе влияния скважины, а также фильтрационные характеристики
пьезоповодность ![]() и проницаемость
и проницаемость ![]() предполагаются известными величинами.
предполагаются известными величинами.
Функция ![]() в области D должна удовлетворять следующим условиям:
в области D должна удовлетворять следующим условиям:
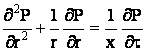 . (1)
. (1)
![]()
![]() .
.
![]() . (2)
. (2)
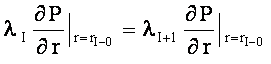 . (3)
. (3)
![]() ,
, ![]() ; (4)
; (4)
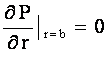 ,
, ![]() , (5)
, (5)
![]() ,
, ![]() ,
(6)
,
(6)
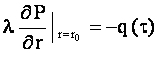 ,
, ![]() (7)
(7)
В качестве дополнительной входной информации заданы давления ![]() в точках
в точках ![]() ( м – число датчиков давления в пъезометрических скважинах, которые
могут быть приняты расположенными в рассматриваемом направлении).
( м – число датчиков давления в пъезометрических скважинах, которые
могут быть приняты расположенными в рассматриваемом направлении).
Начальное и граничное условия считаем согласованными между собой
![]() ,
, ![]() (8)
(8)
Сведение математической модели к квазилинейному уравнению теплопроводности
позволяет сформулировать обратную задачу в терминах оптимального
управления для систем с распределенными параметрами, рассматривая
в качестве управляющего воздействия поток ![]() . Для решения задачи (1)–(8) в форме оптимального
управления сформулируем критерий оптимальности. Будем выбирать управление
. Для решения задачи (1)–(8) в форме оптимального
управления сформулируем критерий оптимальности. Будем выбирать управление
![]() из условия
определенной согласованности известных данных
из условия
определенной согласованности известных данных ![]() с расчетными значениями давления
с расчетными значениями давления ![]() ,
соответствующими выбранному управлению.
,
соответствующими выбранному управлению.
Выберем в качестве меры уклонения среднюю квадратичную невязку
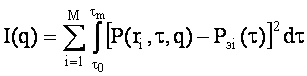 (9)
(9)
Величина I(q) представляет собой функционал в пространстве функций
![]() , и его численное значение определяет расстояние
в функциональном пространстве между заданными экспериментальными
и рассчитанными данными.
, и его численное значение определяет расстояние
в функциональном пространстве между заданными экспериментальными
и рассчитанными данными.
Для того чтобы завершить постановку экстремальной задачи, необходимо
определить допустимое множество функций управления Q и считать,
что все управляющие воздействия принадлежат этому множеству ![]() .
Область допустимых решений можно выделить на основании априорной
информации из чисто физических соображений, задавая диапазон возможных
значений потока и вид зависимости
.
Область допустимых решений можно выделить на основании априорной
информации из чисто физических соображений, задавая диапазон возможных
значений потока и вид зависимости ![]() .
.
В общем случае для построения аппроксимирующей зависимости ![]() целесообразно воспользоваться методом последовательных интервалов.
Решение обратной задачи с помощью этого метода при потоке с меняющейся
во времени плотностью заключается в разбиении рассматриваемого периода
времени на интервалы, в каждом из которых функция, входящая в граничное
условие, принимается постоянной, а при ступенчатой аппроксимации
– непрерывной функцией
целесообразно воспользоваться методом последовательных интервалов.
Решение обратной задачи с помощью этого метода при потоке с меняющейся
во времени плотностью заключается в разбиении рассматриваемого периода
времени на интервалы, в каждом из которых функция, входящая в граничное
условие, принимается постоянной, а при ступенчатой аппроксимации
– непрерывной функцией ![]() и выражается зависимостью
и выражается зависимостью
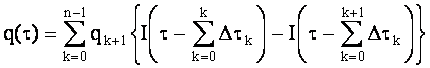 , (10)
, (10)
где ![]() – единичная функция Хевисайда.
– единичная функция Хевисайда.
При этом на каждом интервале времени выполняется равенство
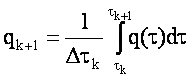 .
.
Минимизации функционала невязки в дальнейшем осуществляется варьированием параметров q(k) в выражении (10)
Для осуществления регулярности процесса вычисления представляют итерационные алгоритмы оптимизации, с помощью которых происходит последовательное уточнение решения в соответствии с формулой
![]()
где ![]() – начальное приближение.
– начальное приближение.
Поправку ![]() на каждой итерации рассчитывают из условия убывания
целевого функционала
на каждой итерации рассчитывают из условия убывания
целевого функционала ![]() .
Такой способ демпфирования неустойчивости при определении приближенного
решения некорректной задачи основывается на вязкостных свойствах
численных алгоритмов минимизации.
.
Такой способ демпфирования неустойчивости при определении приближенного
решения некорректной задачи основывается на вязкостных свойствах
численных алгоритмов минимизации.
По мере увеличения числа итераций решение обратной задачи может
ухудшаться, постепенно теряя гладкий характер. Эта особенность обратных
задач в наибольшей степени проявляется в граничных обратных задачах.
Появляющаяся «разболтанность» в решении ![]() будет прослеживаться тем заметнее, чем большими флуктуационными
погрешностями отягощены входные данные и чем больше расстояние между
границей с искомым условием
будет прослеживаться тем заметнее, чем большими флуктуационными
погрешностями отягощены входные данные и чем больше расстояние между
границей с искомым условием ![]() и точкой измерения давления
и точкой измерения давления ![]() . Поэтому нет необходимости пытаться выявлять
оптимальную точку с точностью выше точности задания входных данных.
Необходимо выбрать допустимый уровень минимизации, являющийся критерием
останова итерационного процесса. В качестве такого критерия примем
ограничение на уровень невязки:
. Поэтому нет необходимости пытаться выявлять
оптимальную точку с точностью выше точности задания входных данных.
Необходимо выбрать допустимый уровень минимизации, являющийся критерием
останова итерационного процесса. В качестве такого критерия примем
ограничение на уровень невязки:
![]() ;
; ![]() (11)
(11)
при условии, что любая из функций ![]() ,
соответствующих границе множества
,
соответствующих границе множества
![]()
и полученных от разных достаточно гладких начальных приближений
![]() , отличается от истинного решения
, отличается от истинного решения ![]() в пределах допустимой точности.
в пределах допустимой точности.
Величина ![]() оценивается по формуле
оценивается по формуле
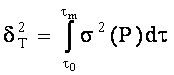 ,
,
где ![]() – дисперсия функции
– дисперсия функции ![]() .
.
Ошибку аппроксимации ![]() определить довольно сложно, однако обычно
определить довольно сложно, однако обычно ![]() . Поэтому можно принять
. Поэтому можно принять ![]() .
.
Для решения обратных задач в трактовке оптимального управления широко применяются градиентные методы. Возможность успешного использования этих методов связана с тем, что процесс уточнения искомого решения вначале происходит быстро, мало зависит от ошибок входных данных и погрешностей вычислений и резко замедляется по мере приближения к оптимальной точке. В результате, с одной стороны, преодолевается одна из основных трудностей оптимизации, связанная с выбором достаточно близкого начального приближения, а с другой –, появляется реальная возможность, используя вязкостные свойства алгоритмов, получить гладкие решения обратной задачи.
Реализация градиентных методов приводит к созданию эффективных вычислительных алгоритмов, отличающихся простотой, малыми затратами машинного времени и способностью надежного определения достаточно близких приближений к искомым функциям.
Численная апробация предложенного подхода показала, с одной стороны, устойчивость и сходимость алгоритма, возможность использования для идентификации фильтрационных характеристик призабойной зоны экспериментальных данных об изменении давления в различных нестационарных режимах эксплуатации скважины, не ограниченных краевыми условиями имеющихся аналитических решений, с другой – подтвердила существенное влияние на достоверность и единственность решения обратной задачи объема и дисперсии экспериментальных данных о динамике давления в скважине.
Для повышения качества и количества экспериментальной информации специалистами кафедры ВТ и АСУ Кубанского государственного технологического университета разработан автономный погружной внутрискважинный измеритель давления и температуры ВИД-1. После подъема измерителя из скважины он подключается через модуль сопряжения к компьютеру, осуществляется считывание информации с запоминающего устройства, восстановление по тарировочным характеристикам датчиков кривых изменения во времени давления и температуры.
Программное обеспечение, реализующее предложенный выше алгоритм решения обратной задачи, и измеритель давления и температуры ВИД-1 в целом составляют автоматизированную систему идентификации параметров математической модели нестационарной фильтрации в скважине.
В настоящее время данная система проходит опытную промысловую эксплуатацию.
1. Базлов М.Н., Жуков А.И., Чернов Б.С. Гидродинамические исследования скважин. М., 1975. 380 с.
Научный электронный журнал КубГАУ . № 01(1), 2003