Научный электронный журнал КубГАУ . № 01(1), 2003
Нелинейная динамика физически линейной и нелинейной вязкоупругой пластины
Аршинов Г.А.
Кубанский государственный аграрный университет
Метод возмущений применяется для исследования дисперсионных волн
в геометрически нелинейной пластине из линейно- и нелинейно-вязкоупругого
материала. Выведены эволюционное уравнения Кадомцева – Петвиашвили
– Бюргерса для физически линейной и модифицированное уравнение для
физически нелинейной пластины.
Рассматривается бесконечная пластина толщиной 2h, свободная от внешних воздействий. Компоненты вектора перемещений точек пластины при симметричных по толщине колебаниях и невысоких частотах зададим соотношениями [1]:
![]()
![]() v
v![]() ;
;
![]() , (1)
, (1)
в которых ![]() и v
и v![]() - функции, определяющие поле перемещений в срединной плоскости по
осям
- функции, определяющие поле перемещений в срединной плоскости по
осям ![]() и
и ![]() соответственно;
соответственно; ![]() - перемещения по оси ;
- перемещения по оси ; ![]() - время.
- время.
Используя кинематические соотношения (1) и формулы Лагранжа для конечных деформаций
![]() (2)
(2)
вычислим компоненты тензора деформаций.
Реологические свойства пластины зададим уравнениями линейной теории вязкоупругости, содержащими экспоненциальное ядро вида[2].
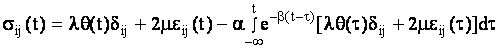 , (3)
, (3)
где ![]() - соответственно компоненты тензоров напряжений и деформаций;
- соответственно компоненты тензоров напряжений и деформаций;
![]() - объемное
расширение;
- объемное
расширение; ![]() - символы Кронекера;
- символы Кронекера; ![]() - реологические параметры;
- реологические параметры;
![]() - упругие постоянные Ламе.
- упругие постоянные Ламе.
Уравнения движения пластины получим, применяя вариационный принцип
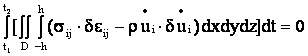 , (4)
, (4)
где ![]() - плотность материала пластины;
- плотность материала пластины; ![]() - вариации деформаций;
- вариации деформаций; ![]() - вариации перемещений; точкой обозначена производная
по времени.
- вариации перемещений; точкой обозначена производная
по времени.
В результате вычисления компонент деформаций (2) на основе функций
(1), вариаций ![]() затем компонент тензора напряжений
затем компонент тензора напряжений ![]() из закона состояния (3) и подстановки
найденных величин в уравнение (4), из последнего в силу произвольности
вариаций
из закона состояния (3) и подстановки
найденных величин в уравнение (4), из последнего в силу произвольности
вариаций ![]() после интегрирования по переменной z получаем интегро-дифференциальные
уравнения движения пластины:
после интегрирования по переменной z получаем интегро-дифференциальные
уравнения движения пластины:
![]() =
= 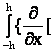
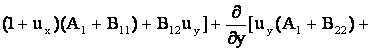
![]() .
.
![]() v =
v = 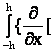 vx
vx![]() vy)] +
vy)] + 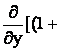 vy)
vy)![]()
![]()
![]() .
.
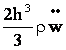 =
= 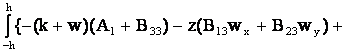 (5)
(5)
+ ![]()
![]() +
+
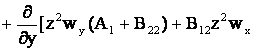
![]() ,
,
где введены следующие обозначения:
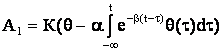 (6)
(6)
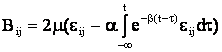 , (7)
, (7)
![]() - поправочный коэффициент, а К – модуль объемного
расширения.
- поправочный коэффициент, а К – модуль объемного
расширения.
Буквенные индексы в системе (5), как и ранее, определяют производную по соответствующей переменной.
Заменим интегральные операторы в формулах (6) и (7) дифференциальными,
разлагая функции ![]() ,
, ![]() в ряды Тейлора по степеням (
в ряды Тейлора по степеням (![]() ), сохраняя в полученных разложениях два слагаемых,
что допустимо для
), сохраняя в полученных разложениях два слагаемых,
что допустимо для ![]() .
.
В результате получим аппроксимации:
![]() ,
, ![]() , (8)
, (8)
где введены операторы
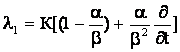 ,
, 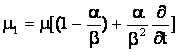 ,
,
действующие на функцию ![]() по правилу
по правилу
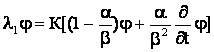 ,
, 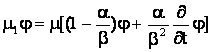 .
.
Обозначим через А амплитуду колебаний, а через l - длину волны
и рассмотрим длинные волны малой амплитуды, вводя таким образом
малый параметр ![]() . Заменим в системе (5)
. Заменим в системе (5) ![]() и
и ![]() их приближениями (8) и исследуем полученные уравнения
асимптотическим методом. Для этого перейдем в полученных уравнениях
к безразмерным переменным
их приближениями (8) и исследуем полученные уравнения
асимптотическим методом. Для этого перейдем в полученных уравнениях
к безразмерным переменным
![]()
![]() , v =
, v = ![]() v*,
v*, ![]()
![]() ,
, ![]() ,
, ![]() .
(9)
.
(9)
Представим неизвестные функции асимптотическими разложениями, опуская звездочки при соответствующих безразмерных переменных:
![]()
v = ![]() (v1 + v2 +…) (10)
(v1 + v2 +…) (10)
![]()
![]()
Допустим, что величины ![]() ,
, ![]() ,
, ![]() - одного порядка малости и подставим разложения (10)
в безразмерные уравнения пластины. Учитывая введенные отношения
порядков, для первых членов разложения получим систему уравнений:
- одного порядка малости и подставим разложения (10)
в безразмерные уравнения пластины. Учитывая введенные отношения
порядков, для первых членов разложения получим систему уравнений:
![]() , (11)
, (11)
![]() = 0. (12)
= 0. (12)
Из уравнения (12) следует, что
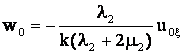 (13)
(13)
где 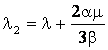 ,
, 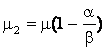 .
.
Из уравнения (4.11) в силу формулы (4.13) определим скорость волны
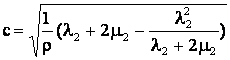 (14)
(14)
Для вторых членов разложений (10 )получим систему трех уравнений
![]() v
v![]() +
+ ![]()
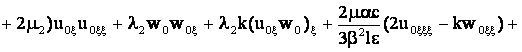
![]() , (15)
, (15)
![]() v
v![]() =
= ![]() v
v![]() +
+ ![]() , (16)
, (16)
 v
v![]() ) +
) + 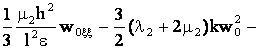
![]()
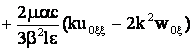 (17)
(17)
После интегрирования уравнения (16) по переменной ![]() и применения формулы (13), приходим к равенству v
и применения формулы (13), приходим к равенству v![]() =
= ![]() .В силу последнего равенства и формулы (13) уравнение
(17) после его дифференцирования по
.В силу последнего равенства и формулы (13) уравнение
(17) после его дифференцирования по ![]() приведем к виду:
приведем к виду:
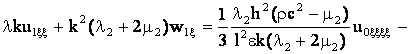
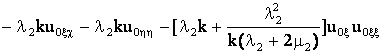 + (18)
+ (18)
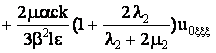
Учитывая формулу (14), легко установить, что последние три слагаемых
в уравнении (15) равны левой части уравнения (18), умноженной на
величину 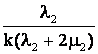 .
.
Приравнивая соответствующие слагаемые, получаем
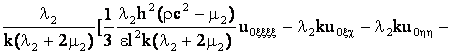
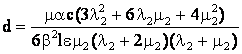
![]() v
v![]() +
+![]() + (19)
+ (19)

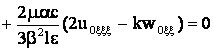
Выполняя тождественные преобразования в уравнении (19) и вводя
обозначение ![]() , приходим к уравнению Кадомцева – Петвиашвили
– Бюргерса
, приходим к уравнению Кадомцева – Петвиашвили
– Бюргерса
![]() , (20)
, (20)
где введены обозначения
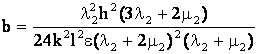 ,
,
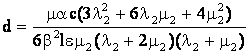 .
.
Перейдем к рассмотрению физически нелинейной вязкоупругой пластины.
Как и в линейном случае, рассмотрим неограниченную пластину толщиной
![]() , свободную от внешних воздействий, а перемещения точек
пластины аппроксимируем функциями
, свободную от внешних воздействий, а перемещения точек
пластины аппроксимируем функциями
![]()
![]() v
v![]() ;
; ![]() (21)
(21)
Используя (21) и тензор деформаций Лагранжа
![]() , (22)
, (22)
вычислим компоненты тензора конечных деформаций.
Реологические свойства пластины зададим уравнениями квадратичной теории вязкоупругости, содержащими экспоненциальное ядро [2].
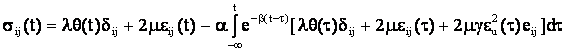 ,(23)
,(23)
![]()
где ![]() - соответственно компоненты тензоров напряжений
и деформаций,
- соответственно компоненты тензоров напряжений
и деформаций, ![]() - объемное расширение,
- объемное расширение, ![]() - компоненты девиатора деформаций,
- компоненты девиатора деформаций, ![]() - символы Кронекера,
- символы Кронекера, ![]() - реологические параметры,
- реологические параметры, ![]() - упругие постоянные Ламе,
- упругие постоянные Ламе, ![]() - квадрат интенсивности деформаций.
- квадрат интенсивности деформаций.
В результате вычисления компонент деформаций (22) на основе функций
(21), вариаций ![]() затем компонент тензора напряжений
затем компонент тензора напряжений ![]() из закона состояния (23) и подстановки
найденных величин в уравнение (4), из последнего в силу произвольности
вариаций
из закона состояния (23) и подстановки
найденных величин в уравнение (4), из последнего в силу произвольности
вариаций ![]() после интегрирования по переменной z получаем интегро-дифференциальные
уравнения движения пластины:
после интегрирования по переменной z получаем интегро-дифференциальные
уравнения движения пластины:
![]() =
= 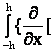
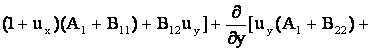
![]()
![]() v =
v = 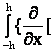 vx
vx![]() vy)] +
vy)] + 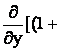 vy)
vy)![]()
![]()
![]()
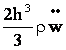 =
= 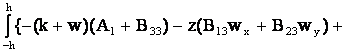 (24)
(24)
+ ![]()
![]() +
+
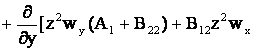
![]() ,
,
где введены следующие обозначения:
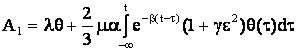 (25)
(25)
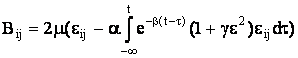 , (26)
, (26)
а ![]() - поправочный коэффициент.
- поправочный коэффициент.
Упростим дальнейшее исследование системы (24), заменяя интегральные
операторы в формулах (25) и (26) дифференциальными путем разложения
функций ![]() ,
, ![]() , в ряды Тейлора по степеням (
, в ряды Тейлора по степеням (![]() ), сохраняя в полученных разложениях
два слагаемых, что возможно для
), сохраняя в полученных разложениях
два слагаемых, что возможно для ![]() .
.
В результате получим приближения
![]() ,
, ![]() , (27)
, (27)
где введены операторы
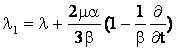 ,
, 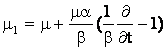 ,
,
действующие на функцию ![]() по правилу
по правилу
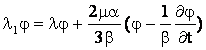 ,
,
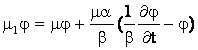 .
.
Для исследования уравнений движения (24) применим асимптотический
метод. Обозначим через ![]() амплитуду колебаний, а через
амплитуду колебаний, а через ![]() - длину волны и рассмотрим длинные волны малой амплитуды,
вводя таким образом малый параметр
- длину волны и рассмотрим длинные волны малой амплитуды,
вводя таким образом малый параметр ![]() . Заменим в системе (24)
. Заменим в системе (24) ![]() и
и ![]() их приближениями (27) и перейдем в полученных
уравнениях к безразмерным переменным
их приближениями (27) и перейдем в полученных
уравнениях к безразмерным переменным
![]()
![]() , v =
, v = ![]() v*,
v*, ![]()
![]() ,
, ![]() ,
, ![]() .
(28)
.
(28)
Представим искомые функции в виде следующих асимптотических разложений, опуская звездочки при соответствующих безразмерных переменных:
![]()
v = ![]() (v1 + v2 +…) (29)
(v1 + v2 +…) (29)
![]()
![]()
Допустим, что величины ![]() ,
, ![]() ,
, ![]() - одного порядка малости, а реологическая постоянная
- одного порядка малости, а реологическая постоянная
![]() - порядка
- порядка
![]() .
.
Подставляя разложение (29) в безразмерные уравнения пластины и учитывая введенные отношения порядков, для первых членов разложения получаем
![]() , (30)
, (30)
![]() = 0, (31)
= 0, (31)
Из уравнения (31) следует, что
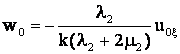 (32)
(32)
где 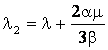 ,
, 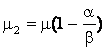 .
.
Из уравнения (30) в силу равенства (32) определяем скорость
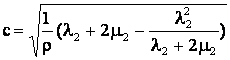 (33)
(33)
Для следующих членов разложений (29) получим систему трех уравнений
![]() v
v![]() +
+ ![]()
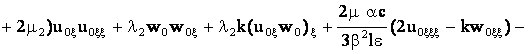
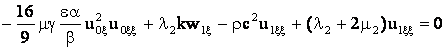 (34)
(34)
![]() v
v![]() =
= ![]() v
v![]() +
+ ![]() (35)
(35)
 v
v![]() ) +
) + 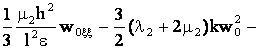
![]()
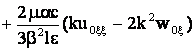 (36)
(36)
После интегрирования уравнения (35) по переменной ![]() и применения формулы (32), приходим к равенству v
и применения формулы (32), приходим к равенству v![]() =
= ![]() .В силу этого равенства и формулы (32) уравнение (36)
после его дифференцирования по
.В силу этого равенства и формулы (32) уравнение (36)
после его дифференцирования по ![]() приведем к виду
приведем к виду
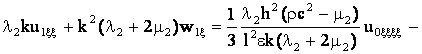
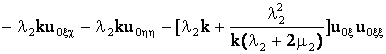 + (37)
+ (37)
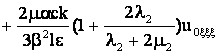
Учитывая формулу (33), легко видеть, что последние три слагаемых
в уравнении (35) равны левой части уравнения (37), умноженной на
величину 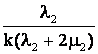 .
.
Приравнивая соответствующие слагаемые, получаем
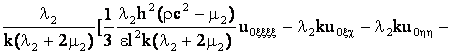
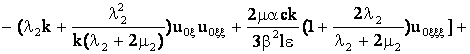
![]() v
v![]() +
+![]() + (38)
+ (38)

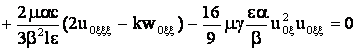
Выполняя преобразования в уравнении (38) и вводя обозначение ![]() , приходим к модифицированному уравнению Кадомцева –
Петвиашвили – Бюргерса
, приходим к модифицированному уравнению Кадомцева –
Петвиашвили – Бюргерса
![]() , (39)
, (39)
где введены обозначения
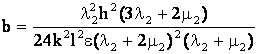 ,
,
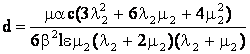 ,
,
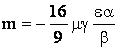 .
.
Список литературы
1. Аршинов Г.А., Могилевич Л.И. Статические и динамические задачи вязкоупругости. Саратов: Изд-во СГАУ, 2002. 152 с.
2. Москвитин В.В. Сопротивление вязкоупругих материалов. М., 1972.
Научный электронный журнал КубГАУ . № 01(1), 2003