Научный электронный журнал КубГАУ . № 01(1), 2003

Управление экономикой перерабатывающего комплекса

В.В. Крохмаль, В.И. Лойко

Краснодар

При интегральном подходе в логистике материальный поток рассматривается в качестве интегратора, причем интегрирующая функции может распространяться на несколько объектов. Необходимым условием является взаимодействия указанных объектов либо с управляемым материальным потоком непосредственно, либо опосредованно - через информационные или финансовые потоки. Эта концепция реализована в разработанных авторами статьи экономико-математических моделях АПК как макро, так и микро уровня.

На Западе логистическая концепция в современном понимании возникла в конце 50-х годов ХХ века и первоначально была связана с оптимизацией технологического цикла производства продукции, в частности, сокращением основного производственного времени и минимизацией уровней производственных запасов сырья и материалов. За последние годы логистика как наука сформировалась в результате относительно длительной эволюции и взаимного проникновения таких научных дисциплин и концепций, как организация снабжения и сбыта, операционный менеджмент, маркетинг, материальное планирование, физическое распределение и ряд других. Научную базу логистики составили многочисленные разделы и направления технической и экономической кибернетики, теория управления, методы и модели оптимизации (в частности, математическое программирование), экономико-математическое моделирование, теория систем, теория управления запасами и другие методы исследования операций.

Сущность нового, интегрального подхода к логистике заключается в рассмотрении ее как некоего синтетического инструмента, интегрированного материальным потоком для достижения поставленных целей [2, 5].

При интегральном подходе материальный поток рассматривается в качестве интегратора, причем интегрирующая функции может распространяться на несколько предприятий, организаций, логистических посредников, обобщенных функций, компьютерных информационных систем и финансовых институтов. Единственно необходимым условием является наличие взаимодействия указанных объектов либо с управляемым материальным потоком непосредственно, либо опосредованно - через информационные или финансовые потоки.

Таким образом, в производственных интегрированных логистических системах материальный поток рассматривается в более активном смысле, объединяющем весь жизненный цикл изделия: от идеи к производству, затем распределению, продаже, послепродажному сервису и вновь к повторному циклу в соответствии с меняющимися запросами потребителей.

Макроэкономический анализ системы АПК

При моделировании реструктуризации крупных производственных объединений со значительным пространственным удалением структурных подразделений друг от друга (агропредприятия, предприятия перерабатывающей промышленности, крупные предприятия материально-технического снабжения) организация движения материальных и сопутствующих им информационных и финансовых потоков оказывает решающее влияние на эффективность их структуры. Поэтому при изучении экономических процессов подобных предприятий логистический подход может быть методологической основой их исследования [5].

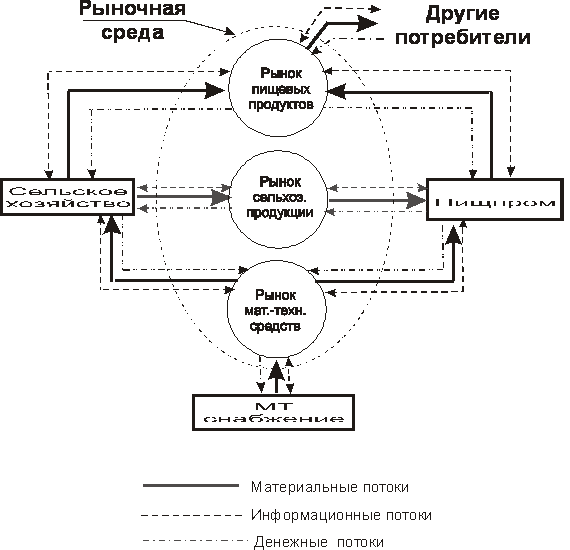
С точки зрения интегральной логистической концепции, АПК на макроуровне представляется в виде трех крупных блоков – подсистем (сельское хозяйство, перерабатывающая промышленность и материально-техническое снабжение), связанных между собой через рыночную среду логистическими потоками и сопутствующими им информационными и финансовыми потоками (рис. 1). Через рынок происходит взаимное преобразование этих потоков по известной формуле «деньги – товар - деньги». Математическое описание такой системы с помощью традиционных подходов не дает обозримое динамическое и статическое ее описание с целью реализации управления системой.

Одним из новых подходов, позволяющих выделить управляемые параметры макросистемы и получить их функциональную взаимосвязь, является подход, развиваемый проф. А.А. Денисовым [3]. Этот подход базируется на формализации законов диалектики и теории цепей. Формализуются такие законы диалектики, как закон об обратной зависимости между объемом понятия и его содержанием, закон изменчивости, понятие тезиса и антитезиса, закон единства противоположностей, закон отрицания отрицания, закон перехода количественных изменений в качественные. Логистические взаимосвязи подсистем АПК, осуществляемые через общий рынок, описываются через аппарат теории цепей, позволяющий с помощью законов Киргофа и Ома составить оригинальную логистическую модель взаимодействия подсистем АПК (рис.2). Применение дифференциальной формы закона Ома дает возможность получить динамические и переходные характеристики процессов, протекающих в АПК [4].

Схематично процедура товарно-денежного обращения выглядит так, как показано на рис. 2.

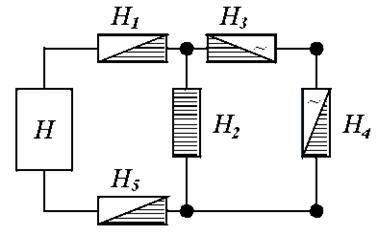
На этой схеме Н = Н₀ – ΔН, где Н₀  эффективность (или потенциал) экономики, ΔН, - капиталовложения.

На рис. 2 горизонтальной штриховкой выделены участки обращения товара, без цвета - участки обращения труда, а волнистым знаком - участки обращения денег. В блоке «производство» труд превращается в товар, придавая ему свою стоимость Н₁. В блоке «бартер» затраты труда на обмен товаров придают им прибавочную стоимость Н₂, которая на современном рынке распределяется между блоками «продажа» и «покупка», так что , где Н₃ оптовая наценка, Н₄ - розничная наценка. Таким образом, цена товара составляет ΔН + Н₁ + Н₃ + Н₅. В блоке "потребление" товар идет на воспроизводство труда (рабочей силы), сохраняя за собой потребительную стоимость Н₅, которую обычно именуют "спросом". Таким образом, .

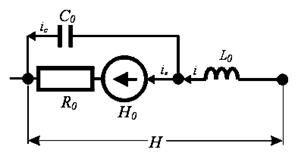
Согласно А.А. Денисову любой экономический процесс может быть представлен эквивалентной RLC – цепью вида, показанного на рис. 3.

В этой цепи R – нормированное время протекания процесса (сопротивление процессу); C – емкость процесса; L – ригидность процесса, (квадрат времени становления процесса).

Для блока экономической эффективности в цепь рис. 3 добавляется источник эффективности (рис. 4)

Каждая структурная составляющая системы АПК может быть представлена в виде схемы рис. 2 . Тогда упрощенная схема логистических процессов АПК будет иметь вид рис. 5.

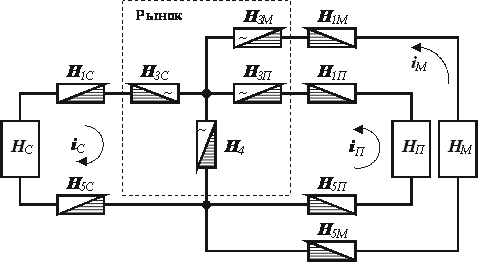
На схеме рис.5 введены следующие обозначения: H_k=(H_ok-ΔH_k) - экономический потенциал (эффективность) блока системы; H_1k  - процесс производства k–го блока системы (труд-товар); H_2k  - процесс бартерного обмена k –го блока (товар-товар); H_3k  - процесс продажи продукции k –го блока (товар-деньги); H₄ - процесс покупок товаров на общем рынке (деньги- товар); H_5k  - процесс потребления k –го блока (товар-труд); k Є L; L= c, п, м, где с – сельское хозяйство, п– пищеперерабатывающая промышленность, м – материально-техническое снабжение; i_k  - оборот стоимостей в k –м блоке АПК.

В схеме цепи логистических процессов АПК, изображенной на рис. 5, процессы H_2k, H_3k и общий H₄ образуют цепь процессов, протекающих на рынке.

На схеме рис. 5 процесс H₄ представляет собой общий процесс покупок, протекающий параллельно на всех специализированных рынках, на которых покупают производители АПК. Любой из изображенных на рис. 5 процессов может быть заменен RLC-цепью рис. 3 или рис. 4.

Очевидно, что для экономики с установившимися экономическими процессами, анализ цепи значительно упрощается, поскольку дифференциальное уравнение цепи приобретает алгебраическую форму, а внешние воздействия не зависят от времени. Для переходной экономики, каковой является экономика России, установившийся процесс длится ограниченное время, после чего возникает либо скачкообразное внешнее возмущение, либо скачкообразное изменение параметра одного или нескольких элементов экономической цепи. Следствием подобных скачков является возникновение переходных процессов, после протекания которых экономическая система переходит в новое устойчивое состояние.

Учитывая сказанное об особенностях переходной экономики, можно предложить следующую двухэтапную методику анализа экономической системы, и системы АПК в частности, по ее моделирующей экономической цепи.

1-й этап. Анализ установившегося режима цепи:

а) составление системы алгебраических уравнений экономического равновесия цепи;

б) разрешение системы относительно выбранной ветви;

в) анализ полученного решения.

2-й этап. Анализ переходных процессов цепи:

а) анализ реакции экономической цепи на скачок источника экономического потенциала;

б) анализ реакции экономической цепи на скачок параметра элемента цепи.

При выполнении пунктов а) и б) второго этапа может быть использована одна из методик анализа переходных процессов в линейных инвариантных во времени цепях.

В установившемся режиме в экономической цепи действуют постоянные во времени обороты стоимостей и экономические потенциалы. В этом режиме реактивные составляющие процессов не оказывают влияния. Тогда система топологических уравнений цепи будет иметь вид:

ΔН_с+Н_1с+Н_3с+Н₄+Н_5с=Н_с

ΔН_п+Н_1п+Н_3п+Н₄+Н_5п=Н_п

Н_п-(ΔН_п+Н_1п+Н_3п)=Н_м-(ΔН_м+Н_1м+Н_3м)

I_c+I_м+I_м=I₄

К этим уравнениям добавятся 13 компонентных уравнений вида

H = IR.

Эти 17 независимых уравнений представляют собой систему уравнений равновесия экономической цепи АПК, и позволяют при заданных экономических потенциалах (эффективностях) источников и сопротивлениях процессов определить значения приведенных стоимостей Н всех процессов и их оборотов I.

Устойчивость (сбалансированность) экономики подразумевает равенство производства и потребления (доходов и расходов), из чего следует, что в установившемся режиме для баланса экономики любой подсистемы (контура) АПК рис. 5 должно быть: ΔН_k+Н_{1 k}+Н_{3 k}+Н₄ = Н_{5 k} =.

Если выделить в одном из контуров искомый процесс, например прибыль производителя товаров R₃, то мощность прибыли производителя N₃ составит:

N₃ = H₃I₃ = I ²R ₃ = ,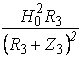

где Z₃=R₀+R₁+R₄+R₅.

Солидарная максимальная прибыль достигается при

R₃=R₄ , (1)

то есть у всех подсистем сопротивления продаж R₃   должны быть равны общему сопротивлению покупок R₄, что эквивалентно равенству оптовых и розничных наценок.

При выполнении условия (1) для всех контуров, в них достигаются оптимальные значения оборотов стоимостей, а с учетом условия сбалансированности получим для оптимального оборота I_опт каждого контура

I_опт = 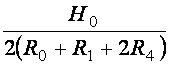  (2)

Учитывая, что R₄ является общим для всех контуров, в выражении (2) третье слагаемое в скобках у всех контуров должно быть одинаковым. Поскольку этот же оборот I_опт идет через сопротивление потребления R₅ и падение потенциала на нем тоже равно , получим:

R₀ + R₁ +2 R_p = R₅.

Откуда для оптимального оборота I_опт, максимизирующего солидарную прибыль производителя и продавца при одновременном соблюдении условия сбалансированности, получим

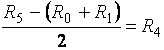. (3)

Для анализа переходных процессов запишем дифференциальное уравнение экономической цепи рис.3:

, (4)

где i  - искомый оборот стоимостей; R, L, C – параметры процесса.

Уравнениями, подобными (4), описываются все экономические процессы АПК, кроме блоков эффективности (полезности) каждой из подсистем. Уравнения этих блоков аналогичны, но в правой части содержат Н₀.

Цепь рис. 5 характеризуется достаточно высоким порядком сложности, и полный анализ ее устойчивости на переходных режимах экономики возможен лишь машинными методами.

Однако, можно сделать некоторые качественные суждения о реакции системы АПК на скачки внешнего воздействия по результатам анализа переходных процессов в отдельном блоке, имеющем лишь второй порядок сложности цепи.

Пусть на цепь экономического процесса (рис. 4) действует источник стоимости, изменяющийся по закону

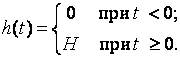
В этом случае получим условия:

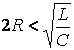 - для апериодического режима;

 для неустойчивого (колебательного) режима.

Другими словами, в переходном режиме экономический процесс имеет апериодический характер, если удвоенное сопротивление обороту стоимости будет меньше корня квадратного из отношения регидности к емкости процесса.

Временная характеристика полного оборота стоимости

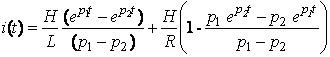. (5)

Первое слагаемое в правой части уравнения (5) – свободная составляющая переходного процесса, второе слагаемое – принужденная составляющая, усложняющая вид переходного процесса. Но поскольку корни характеристического уравнения цепи определяют и ход процесса во втором слагаемом, условие отсутствия колебаний (апериодичности) остается прежним.

В проведенном анализе цепи величина H - это величина скачка, вызванная скачком эффективности (полезности) подсистемы H_к и определяемая коэффициентом передачи для соответствующей ветви. Но в процессе функционирования системы установившийся режим может быть нарушен из-за скачкообразного изменения одного или нескольких сопротивлений обороту. В этом случае переходной процесс в цепи отдельного экономического блока будет протекать аналогично рассмотренному, а величина скачка H может быть определена из анализа установившихся процессов до и после скачка.

Наиболее чувствительными к изменению экономической, финансовой и политической среды в цепи АПК является сопротивление обороту на общем рынке R₄ . Поэтому предположим, что произошло скачкообразное изменение на величину Δ R₄. Так как сопротивление R₄  является общим для всех контуров, то в каждом из них произойдет скачек товарооборота в большую или меньшую сторону в зависимости от знака скачка Δ R₄.

, 

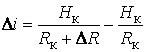где H_к- эффективность соответствующего контура;

R_к=R_0к+R_1к+R_3к+R₄+R_5к - суммарное сопротивление оборота соответствующего контура до скачка.

Скачок же стоимости на R₄ составит

, 

где R₄ - рыночное сопротивление обороту до скачка.

Из выражения для ΔH₄ с очевидностью следует, что завышение цен на общем рынке после окончания переходного процесса вовсе не соответствует ожидаемой прибыли у продавцов, так как ΔR  находится как в числителе, так и в знаменателе.

Чтобы определить ΔR_опт, при котором скачок стоимости ΔH₄ достигает максимума, приравняем производную ΔH₄ по ΔR нулю. Получим ΔR_опт= R₄, т.е. для максимального скачка ΔH₄ прибыли продавцов, необходимо увеличение R₄  в два раза.

Однако, если продавцы решат увеличить в два раза сопротивление обороту (ΔR_опт= R₄), надеясь на двойную прибыль, то в связи с уменьшением товарооборота прирост прибыли составит только

.

Проведенный макроэкономический анализ системы АПК показал, что при использовании формализмов диалектики и теории цепей устанавливаются строгие соотношения между параметрами экономических процессов, и управление ими может осуществляться как изменением эффективностей соответствующих подсистем, так и изменением параметров процессов.

Модель предприятия пищевой и перерабатывающей промышленности

На современном этапе для производства пищевой продукции требуется объединение нескольких разных по производственной направленности агропромышленных предприятий. В этих предприятиях технологический цикл производства пищевых продуктов объединяет материальные, финансовые и информационные потоки [1]. Таким объединением по производству винпродукции является, например, АО «Кубаньвино». Структурная перестройка подобного объединения предполагает, прежде всего, перестройку направлений и объемов материальных и сопутствующих им финансовых потоков, т.е. его логистической системы.

На основе обобщения опыта реструктуризации предприятий пищевой и перерабатывающей промышленности предложена методика их реструктуризации, включающая анализ действующих предприятий, построение структурных схем и математических моделей организации материально-денежных потоков и проведение сравнительного анализа математических моделей.

Разработанная схема и математическая модель организации материально-денежных потоков системы предприятий (на примере производства винопродукции) полнее охватывают технологический процесс производства продукции и минимизируют материально-денежные потоки, что, в свою очередь, существенно уменьшает влияние времени прохождения денежных средств на производство.

Схема реструктурированного предприятия ППП изображена на рис. 6, где: 1- производство мелассы (сахарные заводы); 2- производство спирта (биохимические заводы); 3- производство винограда и виноматериалов (винсовхозы и др. винпредприятия); 4- производство винпродукции (ликеро-водочные заводы); 5- реализация винпродукции (продажа, бартер); 6- базовое предприятие ППП.

Общая сумма С¢ денежных средств базового предприятия ППП, без учета расходов, после завершения цикла

С¢^¢ =(1 + k)^m q₁^¢,

где q₁^¢ – исходный денежный поток (символы со штрихом относятся к реструктурируемому предприятию).

Обозначив долю расходов через Р′ , получим для чистого дохода D′ выражение

D′ = (1 - Р′) С¢ = (1 - Р′) (1 + k)^m q₁^¢.

Эффективность Э предложенной схемы по отношению к ранее существовавшей

Э = .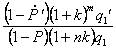

где k – рентабельность; m, n – число циклов «производство-реализация» в предложенной и существовавшей схемах соответственно.

Для выравнивания условий предположим, что доля расходов и исходные денежные средства в обеих схемах одинаковы: Р = Р′ ; q₁ = q₁^¢.

Тогда

Э = .

Если принять норму прибыли k равной 0,25, n=2 и m=4, получим

Э = 1,63,

т.е. чистая прибыль реструктурированной фирмы увеличится на 63%.

Для надежного функционирования предприятий ППК в каждом из них должна быть проведена техническая и материальная подготовка производства, осуществляемая через предприятия материально-технического снабжения. Экономические и политические факторы, повлекшие реструктуризацию предприятий ППП, потребовали реформирования и предприятий материально-технического снабжения.

Модель подсистемы материально-технического снабжения (МТС)

Особое место в логистической системе АПК занимает подсистема МТС, обеспечивающая производственные подсистемы материально-техническими (МТ) ресурсами (рис.7).

Анализ эффективности исходной системы МТС показал, что ей присущи недостатки, которые устраняются реструктурированной системой (рис. 7), где исключены информационные, но детализированы материальные потоки [1].

Эффективность Э ресурсного обеспечения края за один цикл предложенной системы – коммерческо-производственной компанией (КПК) - по сравнению с существовавшей системой МТС определим как:

Э =   ,

где D₁ , D₀– начальный объем денежных средств исходной и предложенной систем; m – число оборотов материальных потоков за один цикл, k – усредненный коэффициент прибыли.

За n циклов в течение года прибыль КПК вычисляется по формуле

П_кп = D_о[(1+ k)^n(m+1)- (1+ k_кр)(1-a)-1]+ k D_пс (1+ k)^(m+1)(i-1) ,

где k_кр – кредитная ставка кредитора, a – относительная доля собственных средств в исходном денежном потоке D₀, D_пс – денежный поток, получаемый от посреднической деятельности в течение одного цикла.

Разделив левую и правую части этого соотношения на D_о, получим выражение для коэффициента прибыли (рентабельности) КПК:

k_кп = (1+ k)^n(m+1) - (1+ k_кр)(1-a)-1+(1+ k)^(m+1)(i-1) .

Из выражений для П_кп  и k_кп видно, что посредническая деятельность, прибыль от которой направляется на увеличение материальных потоков, поступающих на предприятия края, повышая рентабельность КПК, содействует более полному материально-техническому обеспечению производства и сбыта готовой продукции в крае.

Суммарный объем материального потока в системе М_о в этом случае будет эквивалентен (пропорционален)

М_о ~ (1+ k)^i(m+1) +  (n-i)(1+k)^i(m+1).

В общем виде эффективность обеспечения ресурсами края Э за n циклов в течение года по сравнению с исходной системой определится, как

Э = (1+k)^i(m+1)-1 +  (n-i)(1+k)^i(m+1)-1.

В АО КПК «Краснодарглавснаб», где были внедрены разработанные модели, оборот материальных потоков за один цикл m=1, количество циклов в год n=6. коэффициент прибыли установлен на уровне k=0,15. При таких исходных параметрах и предположении, что старая структура имела исходный денежный поток D₁ , равный исходному денежному потоку D_o в реструктурируемой системе, получим частное выражение для эффективности Э:

Э =   = 2,58.

Как видно из этой формулы, структурная перестройка системы КПК позволяет увеличить поставки материальных ресурсов по крайней мере в 2,5 раза.

Если принять D_пс=D₁, т.е. объем посреднического товарооборота за один цикл равным исходному денежному потоку, то Э = 3,25.

Привлечение кредитных ресурсов для функционирования предлагаемой системы организации КПК позволяет существенно увеличивать материальные ресурсы в крае, а, значит, и обеспеченность ими материального производства.

Результирующий материальный поток М₁, поступающий на предприятия региона в конце года, достигнет уровня

М_o~D_o(1+k)^i(m+1)-1+ kD_пс(n-i)(1+k)^i(m+1)-1.

Пеpвый член в правой части выражения для М_o определяется кредитными денежными ресурсами, входящими в состав D_o = .

При объемах кредитов, значительно превышающих собственные средства, коэффициент а=0 и D_o =D_к. Тогда зависимая от кредитов часть (добавлен индекс k) будет

М_ок~D_к(1+k)^i(m+1)-1.

Информационные и материальные потоки ее предприятий должны быть согласованы как с потребителями МТ ресурсов, так и их производителями. С этой целью необходимо создание комплекса моделей (рис. 8), позволяющего оптимизировать наполнение материальных потоков с учетом среды, в которой происходит функционирование предприятия МТ снабжения.

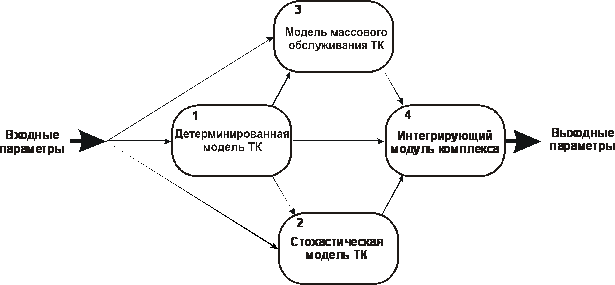
Модели подобного комплекса в своей взаимосвязи должны позволять рассчитывать показатели экономической эффективности и параметры предприятия при триедином подходе – подсистема должна быть представлена как взаимосвязанный комплекс по крайней мере трех основных моделей: детерминированной, основанной на модели Харриса (позволяющей рассчитать «точку заказа» и размер партии поставки), стохастической, дающей возможность скорректировать результаты расчета по детерминированной модели, модели массового обслуживания, учитывающей статистический характер рыночного спроса и позволяющей рассчитать оптимальную структуру предприятия МТС, и , наконец, интегрирующую модель, объединяющую результаты расчетов по первым трем.

Детерминированная модель основана на классической модели Харриса и позволяет определять оптимальный размер партий восстановления запасов, их периодичность и «точки заказов».

Обоснованные и эффективные параметры системы управления запасами определяются также и случайным потоком спроса (потоками заявок) от потребителей.

При создании стохастической модели введен коэффициент издержек g, обусловленный величиной вероятности отказа в обслуживании заявки Р_от. К моменту поставки очередной партии товара существует вероятность Р_i(t) того, что в текущей партии имеется i единиц товара, где i может изменяться от 0 до q^*, где q^* - оптимальный размер партии поставки.

Тогда издержки, обусловленные отказом, определятся выражением

I_от = g [1 -  exp(- q^*)].

Уменьшить издержки отказа I_от возможно за счет упреждающей поставки очередной партии на интервал времени ∆t.

Это приведет к модификации выражения для I_от:

I_от = g [1 - exp(- )],

где d – размер годового спроса.

Однако, такой сдвиг поставок эквивалентен увеличению срока хранения до величины (1 + ∆t) [год], что вызовет увеличенные издержки хранения I_х = h  (1 + ∆t) и общие издержки I = I_х + I_от.

Задача состоит в определении минимальных издержек, обусловленных отказом в обслуживании заявок и издержек хранения, как функции ∆t:

min{I}=g [1 - 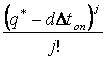exp(- (q^* - d ∆t_оп))] + h (1 + ∆t_оп).

Например, при годовом спросе d = 50 ед., издержках хранения
h = 20 руб./ед., оптимальном размере партии поставки q^* = 7 ед. и издержках отказа в обслуживании g = 100 руб./ед., минимального значения общие издержки достигают при ∆t_оп= 0,1.

В модели массового обслуживания ТК, основанной на аналитической модели многоканальной системы массового обслуживания с ожиданием оценивается качество и эффективность функционирования системы в целях выявления возможности ее улучшения. Функция потерь G_п за интервал времени Т определяется выражением

G_п = (q_с n + q_ожМ + q_уР_отк + q_пкN_п)Т,

где q_ож, q_у, q_пк, q_с, - коэффициенты издержек ожидания в очереди, отказа в обслуживании, простоя канала и содержания канала соответственно;  n - число каналов обслуживания; М - средняя длина очереди; N_п - среднее число простаивающих каналов; Р_отк - вероятность отказа в обслуживании.

Функция прибыли определяется как

Z_n= П_к n_ср – (q_с n + q_ожМ + q_уР_отк + q_пкN_п),

где П_к – прибыль, приносимая одним каналом; n_ср – среднее число занятых каналов (n_ср = n – N_п).

Полученные выражения позволяют определить оптимальное количество каналов обслуживания.

Основное назначение интегрирующего модуля состоит в создании агрегированной выходной информации, определяющей параметры и структуру ТК. Кроме того, в этом же модуле производится корректировка среднего уровня запасов ТК, полученного с помощью детерминированной модели, на основе данных, рассчитанных в стохастической модели ТК.

Внедрение разработанной группы моделей ТК в АО КПК «Краснодарглавснаб» позволило объективно оценить параметры товарных комплексов системы МТС и аргументировано определить объем исходного финансового потока.

Применение интегральной логистической концепции, реализованной на современных моделях и подходах, позволяет усилить эффективность и гибкость управления в системе АПК, и этим ускорить решение социально-экономических задач.

СПИСОК ЛИТЕРАТУРЫ

1.  Барановская Т.П. Модели реформирования предприятий АПК в рыночной экономики. – Краснодар, 2000, издательство КубГАУ. -  218с.: ил.

2.  Колобов А.А., Омельченко И.Н., Шклярский Л.Ф. Логистическое моделирование производственно-сбытовых систем //Вестник машиностроения, 1994, №5, с. 40-43.

3.  Денисов А.А. Макроэкономическое управление и моделирование: Пособие для начинающих реформаторов. - СПб: Омега, 1997, – 37 с.

4.  Лойко В.И. Макроэкономический системный анализ пищеперерабатывающего комплекса. – Краснодар: КубГАУ, 2001. – 42 с., ил.

Научный электронный журнал КубГАУ . № 01(1), 2003