Научный электронный журнал КубГАУ . № 01(1), 2003

СИСТЕМНАЯ ТЕОРИЯ ИНФОРМАЦИИ И НЕЛОКАЛЬНЫЕ ИНТЕРПРЕТИРУЕМЫЕ НЕЙРОННЫЕ СЕТИ ПРЯМОГО СЧЕТА

Луценко Е.В.

Кубанский государственный аграрный университет

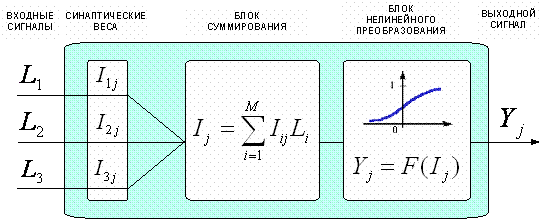
В 1943 году Дж. Маккалоки и У. Питт предложили формальную модель биологического нейрона как устройства, имеющего несколько входов (входные синапсы – дендриты), и один выход (выходной синапс – аксон). Дендриты получают информацию от источников информации (рецепторов) L_i, в качестве которых могут выступать и нейроны. Набор входных сигналов {L_i} характеризует объект или ситуацию, обрабатываемую нейроном. Каждому i-му входу j-го нейрона ставится в соответствие некоторый весовой коэффициент I_ij, характеризующий степень влияния сигнала с этого входа на аргумент передаточной (активационной) функции, определяющей сигнал Y_j на выходе нейрона. В нейроне происходит взвешенное суммирование входных сигналов, и далее это значение используется как аргумент активационной (передаточной) функции нейрона. На рисунке 1 данная модель приведена в обозначениях, принятых в настоящей работе.

Рисунок 1. Классическая модель нейрона Дж. Маккалоки и У. Питта (1943)в обозначениях системной теории информации

Метафора нейросетевого представления семантической информационной модели

В данной работе предлагается представление, согласно которому каждый нейрон отражает определенное будущее состояние активного объекта управления, а нейронная сеть в целом – систему будущих состояний, как желательных (целевых), так и нежелательных. Весовые коэффициенты на дендритах нейронов имеют смысл силы и направления влияния факторов на переход активного объекта управления в то или иное будущее состояние. Таким образом, предложенная в данной работе семантическая информационная модель в принципе допускает представление в терминах и понятиях нейронных сетей. Однако при более детальном рассмотрении выясняется, что семантическая информационная модель является более общей, чем нейросетевая и для полного их соответствия необходимо внести в нейросетевую модель ряд дополнений.

Соответствие основных терминов и понятий

Предлагается следующая система соответствий, позволяющая рассматривать термины и понятия из теории нейронных сетей и предложенной семантической информационной модели практически как синонимы. Нейрон – вектор обобщенного образа класса в матрице информативностей. Входные сигналы – факторы (признаки). Весовой коэффициент – системная мера целесообразности информации. Обучение сети – адаптация модели, т.е. перерасчет значений весовых коэффициентов дендритов для каждого нейрона (матрицы информативностей) и изменение вида активационной функции. Самоорганизация сети – синтез модели, т.е. изменение количества нейронов и дендритов, изменение количества нейронных слоев и структуры связей между факторами и классами, а затем адаптация (перерасчет матрицы информативностей). Таким образом, адаптация – это обучение сети на уровне изменения информационных весовых коэффициентов и активационной функции, а синтез – на уровне изменения размерности и структуры связей нейронов сети. 1-й (входной) слой нейронной сети – формирование обобщенных образов классов. Сети Хопфилда и Хэмминга – обучение с учителем, сопоставление описательной и классификационной информации, идентификация и прогнозирование. 2-й слой, сети Хебба и Кохонена – самообучение, анализ структуры данных без априорной классификационной информации, формирование кластеров классов и факторов. 3-й слой – формирование конструктов (в традиционных нейронных сетях не реализовано). Необходимо отметить, что любой слой нейронной сети является в предлагаемой модели не только обрабатывающим, но и выходным, т.е. с одной стороны дает результаты обработки информации, имеющие самостоятельное значение, а с другой – поставляет информацию для последующих слоев нейронной сети, т.е. более высоких уровней иерархии информационной системы (в полном соответствии с формализуемой когнитивной концепцией).

Недостатки нейронных сетей и пути их преодоления в семантической информационной модели

К основным недостаткам нейронных сетей можно отнести:

1. Сложность содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов").

2. Сложность содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции").

3. "Комбинаторный взрыв", возникающий при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности").

Проблемы интерпретируемости приводят к снижению ценности полученных результатов работы сети, а проблема размерности – к очень жестким ограничениям на количество выходных нейронов в сети, на количество рецепторов и на сложность структуры взаимосвязей нейронов с сети. Достаточно сказать, что количество выходных нейронов в реальных нейронных сетях, реализуемых на базе известных программных пакетов, обычно не превышает несколько сотен, а чаще всего составляет единицы и десятки.

Гипотеза о нелокальности нейрона и информационная нейросетевая парадигма

Модель нелокального нейрона: так как сигналы на дендритах различных нейронов вообще говоря коррелируют (или антикоррелируют) друг с другом, то, значения весовых коэффициентов, а значит и выходное значение на аксоне каждого конкретного нейрона вообще говоря не могут быть определены с использованием значений весовых коэффициентов на дендритах только данного конкретного нейрона, а должны учитывать интенсивности сигналов на всей системе дендритов нейронной сети в целом (рисунок 2).

Рисунок 2. Модель нелокального нейрона в обозначениях системной теории информации

За счет учета корреляций входных сигналов (если они фактически присутствуют в структуре данных), т.е. наличия общего самосогласованного информационного поля исходных данных всей нейронной сети (информационное пространство), нелокальные нейроны ведут себя так, как будто связаны с другими нейронами, хотя могут быть и не связаны с ними синаптически по входу и выходу ни прямо, ни опосредованно. Самосогласованность семантического информационного пространства [3] означает, что учет любого одного нового факта в информационной модели вообще говоря приводит к изменению всех весовых коэффициентов всех нейронов, а не только тех, на рецепторе которых обнаружен этот факт и тех, которые непосредственно или опосредованно синаптически с ним связаны.

В традиционной (т.е. локальной) модели нейрона весовые коэффициенты на его дендритах однозначно определяются заданным выходом на его аксоне и никак не зависят от параметров других нейронов, с которыми с нет прямой или опосредованной синаптической связи. Это связано с тем, что в общепринятой энергетической парадигме Хопфилда весовые коэффициенты дендритов имеют смысл интенсивностей входных воздействий. В методе "обратного распространения ошибки" процесс переобучения, т.е. интерактивного перерасчета весовых коэффициентов, начинается с нейрона, состояние которого оказалось ошибочным и захватывает только нейроны, ведущие от рецепторов к данному нейрону. Корреляции между локальными нейронами обусловлены сочетанием трех основных причин:

– наличием в исходных данных определенной структуры: корреляцией входных сигналов;

– синаптической связью локальных нейронов;

– избыточностью (дублированием) нейронной сети.

Решение проблемы интерпретируемости весовых коэффициентов (семантическая мера целесообразности информации и закон Фехнера)

В данной работе предлагается использовать такие весовые коэффициенты дендритов, чтобы активационная функция была линейной, т.е. по сути была равна своему аргументу: сумме. Этому условию удовлетворяют весовые коэффициенты, рассчитываемые с применением системного обобщения формулы Харкевича [3].

Очень важно, что данная мера, удовлетворяет известному эмпирическому закону Г.Фехнера (1860), согласно которому существует логарифмическая зависимость между интенсивностью фактора и величиной отклика на него биологической системы (в частности, величина ощущения прямо пропорциональна логарифму интенсивности раздражителя).

Предлагается информационный подход к нейронным сетям, по аналогии с энергетическим подходом Хопфилда (1980).

Суть этого подхода состоит в том, что интенсивности входных сигналов рассматриваются не сами по себе и не с точки зрения только их интенсивности, а как сообщения, несущие определенное количество информации или дезинформации о переходе нейрона и моделируемого им активного объекта управления в некоторое будущее состояние.

Под интенсивностью входного сигнала на определенном дендрите мы будем понимать абсолютную частоту (количество) встреч фактора (признака), соответствующего данному дендриту, при предъявлении нейронной сети объекта, соответствующего определенному нейрону. Таким образом матрица абсолютных частот рассматривается как способ накопления и первичного обобщения эмпирической информации об интенсивностях входных сигналов на дендритах в разрезе по нейронам.

Весовые коэффициенты, отражающие влияние каждого входного сигнала на отклик каждого нейрона, т.е. величину его возбуждения или торможения, представляют собой элементы матрицы информативностей, получающиеся из матрицы абсолютных частот методом прямого счета с использованием выражения для семантической меры целесообразности информации [3].

При этом предложенная мера семантической целесообразности информации, как перекликается с нейронными сетями Кохонена, в которых также принято стандартизировать (нормализовать) входные сигналы, что позволяет в определенной мере уйти от многообразия передаточных функций.

Наличие ясной и обоснованной интерпретации весовых коэффициентов, как количества информации, позволяет предложить в качестве математической модели для их расчета системную теорию информации (СТИ).

Семантическая информационная модель, как нелокальная нейронная сеть

Учитывая большое количество содержательных параллелей между семантической информационной моделью и нейронными сетями предлагается рассматривать данную модель как нейросетевую модель, основанную на системной теории информации. В данной модели предлагается вариант решения важных нейросетевых проблем интерпретируемости и ограничения размерности за счет введения меры целесообразности информации (системное обобщение формулы Харкевича), обеспечивающей прямой расчет интерпретируемых весовых коэффициентов на основе непосредственно эмпирических данных. Итак, в данной работе предлагается новый класс нейронных сетей, основанных на семантической информационной модели и информационном подходе. Для этих сетей предлагается полное наименование: "Нелокальные интерпретируемые нейронные сети прямого счета" и сокращенное наименование: "Нелокальные нейронные сети".

Нелокальная нейронная сеть является системой нелокальных нейронов, обладающей качественно новыми (системными, эмерджентными) свойствами, не сводящимися к сумме свойств нейронов. В такой сети поведение нейронов определяется как их собственными свойствами и поступающими на них входными сигналами, так и свойствами нейронной сети в целом, т.е. поведение нейронов в нелокальной нейронной сети согласовано друг с другом не только за счет их прямого и опосредованного синаптического взаимодействия (как в традиционных нейронных сетях), но за счет общего информационного поля весовых коэффициентов всех нейронов данной сети.

Гипотеза о физической природе нелокального взаимодействия нейронов в нелокальной нейронной сети

В данной работе предлагается математическая модель, численный метод и программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос"), успешно апробированные в ряде предметных областей. Данная система обеспечивает неограниченное количество слоев ННС при максимальном количестве весовых коэффициентов в слое до 16 миллионов (в текущей версии 9.0) и до 4000 выходных нейронов. Но если рассматривать нелокальную нейронную сеть как модель реальных "биологических" нейронных сетей, то ясно, что формальной модели недостаточно и необходимо дополнить ее физической моделью о природе каналов нелокального взаимодействия нейронов в данной сети. По мнению автора данный механизм основан на парадоксе Эйнштейна-Подольского Розена (ЭПР) [2, 6, 7]. По мнению автора, физическая реализация нелокальных нейронов может быть осуществлена за счет соединения как минимум одного дендрита каждого нейрона с датчиком микротелекинетического воздействия, на который человек может оказывать влияние дистанционно. Некоторые из подобных датчиков описаны в работе [6]. По мнению автора, мозг может рассматриваться как оптимальная среда для редукции мыслей, в этом смысле квантовые компьютеры, основанные не на математических и программных моделях, а на физических нелокальных нейронах, могут оказаться во многих отношениях функционально эквивалентными физическому организму.

Решение проблемы интерпретируемости передаточной функции

Вопрос об интерпретируемости передаточной функции нейрона включает два основных аспекта: 1) об интерпретируемости аргумента передаточной функции; 2) об интерпретируемости вида передаточной функции.

1. Возникает естественный вопрос о том, чем обосновано включение в состав модели нейрона Дж. Маккалоки и У. Питтом именно аддитивного элемента, суммирующего входные сигналы, а не скажем мультипликативного или в виде какой-либо другой функции общего вида. По мнению автора такой выбор обоснован и имеет явную и убедительную интерпретацию именно в том случае, когда весовые коэффициенты имеют смысл количества информации, т.к. в этом случае данная мера представляет собой неметрический критерий сходства, основанный на лемме Неймана-Пирсона [3]. Сумма весовых коэффициентов, соответствующих набору действующих факторов (входных сигналов) дает величину выходного сигнала на аксоне каждого нейрона.

2. Вид передаточной функции содержательно в теории нейронных сетей явно не обосновывается. Предлагается гипотеза, что на практике вид передаточной функции подбирается таким образом, чтобы соответствовать смыслу подобранных в данном конкретном случае весовых коэффициентов. Так как при применении в различных предметных областях смысл весовых коэффициентов в явном виде не контролируется и может отличаться, то выбор вида передаточной функции позволяет частично компенсировать эти различия.

Предлагаемый интерпретируемый вид весовых коэффициентов обеспечивает единую и стандартную интерпретацию аргумента и значения передаточной функции независимо от предметной области. Поэтому в нелокальной нейронной модели передаточная функция нейрона всегда линейна (аргумент равен функции). Следовательно в модели нелокального нейрона блок суммирования по сути дела объединен с блоком нелинейного преобразования (точнее, второй отсутствует, а его роль выполняет блок суммирования), в отличие от стандартных передаточных функций локальных нейронов: логистической, гиперболического тангенса, пороговой линейной, экспоненциально распределенной, полиномиальной и импульсно-кодовой.

Нелокальные нейроны как бы "резонируют" на ансамбли входных сигналов, причем этот резонанс может быть обоснованно назван семантическим (смысловым), т.к. весовые коэффициенты рассчитаны на основе предложенной семантической меры целесообразности информации. Таким образом, разложение вектора идентифицируемого объекта в ряд по векторам обобщенных образов классов осуществляется на основе семантического резонанса нейронов выходного слоя на ансамбль входных сигналов (признаков, факторов).

Решение проблемы размерности

Вместо итерационного подбора весовых коэффициентов путем полного перебора вариантов их значений при малых вариациях (методы обратного распространения ошибки и градиентного спуска к локальному экстремуму) предлагается прямой расчет этих коэффициентов на основе процедуры и выражений, обоснованных в предложенных системной теории информации и семантической информационной модели. Выигрыш во времени и используемых вычислительных ресурсах, получаемый за счет этого, быстро возрастает при увеличении размерности нейронной сети.

Моделирование причинно-следственных цепочек в нейронных сетях и семантической информационной модели

Факторы описывают причины, а классы – следствия. Но и следствия в свою очередь являются причинами более отдаленных последствий. Предлагаемая семантическая информационная модель позволяет рассматривать события, обнаружение которых осуществляется в режиме идентификации, как причины последующих событий, т.е. как факторы, их вызывающие. При этом факт наступления этих событий моделируется путем включения в модель факторов, соответствующих классам (событиям). В нейронных сетях этот процесс моделируется путем включения в сеть дополнительных нейронных слоев и создания обратных связей между слоями, обеспечивающих передачу в предыдущие слои результатов работы последующих слоев.

Моделирование иерархических структур обработки информации

Рассмотрим иерархическую структуру информации на примере использования психологического теста для оценки психологических качеств сотрудников и влияния этих качеств на эффективность работы фирмы. В нейронной сети иерархическим уровням обработки информации соответствуют слои, поэтому далее будем использовать термины "слой нейронной сети" и "иерархический уровень обработки информации" как синонимы. Рецепторы дают информацию по ответам сотрудника на опросник, нейроны 1-го слоя дают оценку психологических качеств и сигнал с их аксонов является входным для нейронов 2-го слоя, дающих оценку качества работы фирмы. В семантической информационной модели существует три варианта моделирования подобных иерархических структур обработки информации:

1. Заменить все слои одним слоем и выявлять зависимости непосредственно между исходными данными с первичных рецепторов и интересующими итоговыми оценками, например, ответами сотрудников на вопросы и результатами работы фирмы. Этот подход эффективен с прагматической точки зрения, но дает мало информации для теоретических обобщений.

2. Каждый слой моделируется отдельной семантической информационной моделью, включающей свои классификационные и описательные шкалы и градации, обучающую выборку, матрицы абсолютных частот и информативностей. Вся система иерархической обработки информации моделируется системой этих моделей, взаимосвязанных друг с другом по входу-выходу: результаты классификации объектов обучающей выборки 1-й моделью рассматриваются как свойства этих объектов во 2-й модели, в которой они используются для классификации 2-го уровня. Например, психологические качества сотрудников, установленные в результате психологического тестирования, рассматриваются как свойства сотрудников, влияющие на эффективность работы фирмы. Данный подход эффективен и с прагматической, и с теоретической точек зрения, но является громоздким в программной реализации.

3. Моделирование каждого слоя соответствующими подматрицами матриц абсолютных частот и информативностей (таблица).

Этот вариант обладает преимуществами первых двух и преодолевает их недостатки. В нем применяется следующий итерационный алгоритм послойного расчета, где n={1, 2, …, N}, N – количество слоев нейронной сети:

Шаг n: расчет весовых коэффициентов n-го слоя, идентификация объектов обучающей выборки в нейронах n-го слоя, если слой (n+1) существует, то занесение в обучающую выборку в качестве свойств объектов (n+1)-го слоя результатов их идентификации в нейронах n-го слоя.

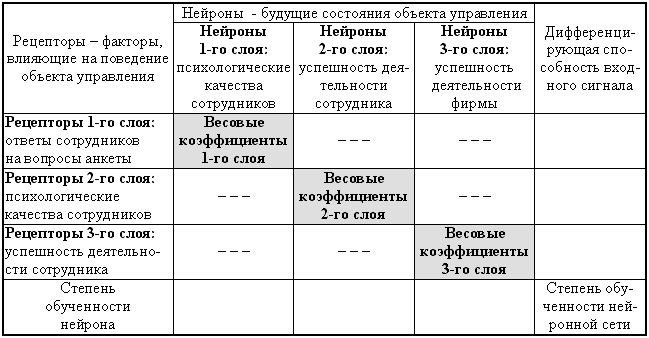
Примечание: в таблице представлена именно логическая структура данных, т.е. в реальных базах данных нет записей, содержащих информацию о влиянии рецепторов n-го слоя на нейроны слоев, номера которых не равны n.

Нейронные сети и СК-анализ

Известные в литературе нейронные сети, в отличие от предлагаемой семантической информационной модели и нелокальных нейронных сетей, не обеспечивают реализацию всех базовых когнитивных операций, входящих в когнитивный конфигуратор. В частности, традиционные нейронные сети решают лишь задачу идентификации (прогнозирования) и не обеспечивают решение обратной задачи (дедукции), необходимой для принятия решения о выборе многофакторного управляющего воздействия. Кроме того не решается вопрос об уменьшении размерности нейронной сети без ущерба для ее адекватности (абстрагирование).

Результаты численного моделирования и исследования свойств нейронных сетей этого класса при управлении в АПК и других предметных областях позволяют предположить, в качестве модели реальных когнитивных процессов они обладает более высокой адекватностью, чем нейронные сети других типов.

Графическое отображение нейронов, Паррето-подмножеств нелокальной нейронной сети, семантических сетей, когнитивных карт и диаграмм в системе "Эйдос"

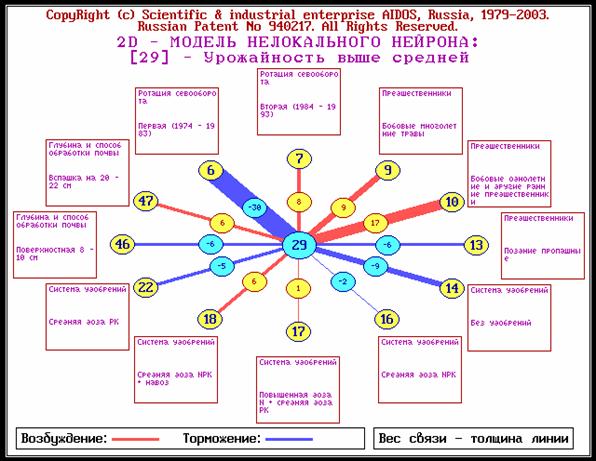
Для каждого технологического фактора в соответствии с предложенной моделью определяется величина и направление его влиянии на осуществление всех желаемых и не желаемых хозяйственных ситуаций. Для каждой ситуации эта информация отображается в различных текстовых и графических формах, в частности в форме нелокального нейрона (рисунок 3).

На данной и последующих графических диаграммах цвет линии означает знак связи (красный – положительная, синий – отрицательная), а толщина – ее модуль.

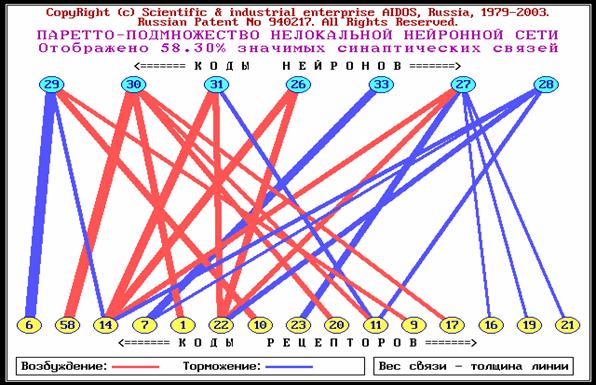
Паретто-подмножеством нелокальной нейронной сети будем называть ее подмножество, включающее наиболее значимые связи. Пример графического отображения такого подмножества приведен а рисунке 4.

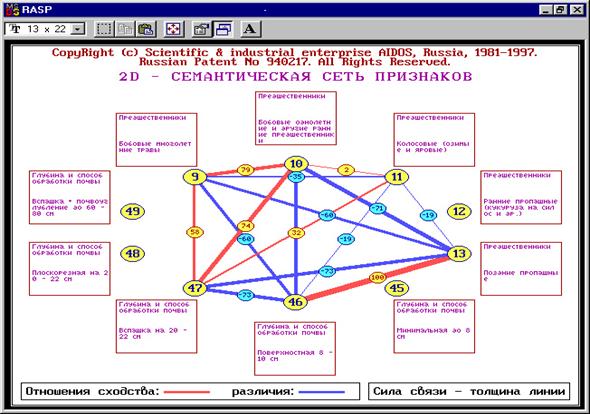
Факторы (сигналы с рецепторов) в модели нелокального нейрона взаимосвязаны друг с другом. Эти связи графически отображаются в форме семантической сети  (рисунок 5).

Дополнение модели нейрона связями факторов позволяет построить классическую когнитивную карту ситуации (будущего состояния АОУ). Детальная внутренняя структура любой связи отображается в форме инвертированной когнитивной диаграммы (рисунок 6). Необходимо отметить, что все указанные графические формы генерируются системой "Эйдос" автоматически в соответствии с созданной моделью.

Рисунок 3. Графическое отображение нелокального нейрона, отражающих влияние факторов на ситуацию, в системе "Эйдос"

Рисунок 4. Графическое отображение Паретто-подмножества нелокальной нейронной сети в системе "Эйдос"
	Рисунок 5. Отображение результатов кластерно-конструктивного анализа факторов в форме семантической сети (когнитивной карты) в системе "Эйдос"

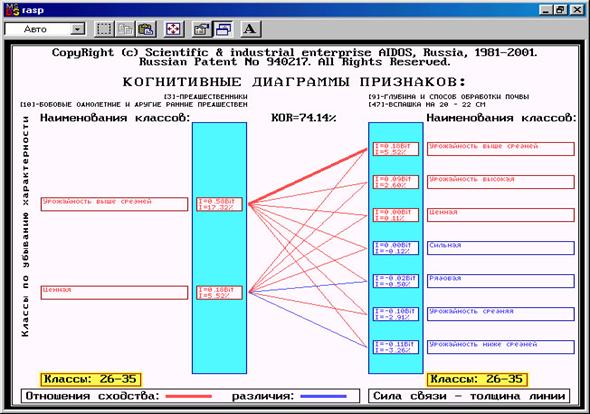Рисунок 6. Когнитивная диаграмма кластера факторов: "Глубина и способ обработки почвы: вспашка на 20-22 см – Предшественники: Бобовые однолетние и другие ранние предшественники", генерируемая системой "Эйдос"

Выводы

Предлагается модель нелокального нейрона, являющаяся обобщением классической модели Дж. Маккалоки и У. Питта. Суть нелокальности данной модели состоит в том, что весовые коэффициенты каждого нейрона зависят не только от нейронов, прямо или косвенно соединенных с ним синаптически, но и от всех остальных нейронов сети, не затрагиваемых при обратном распространении ошибки от данного нейрона. Предлагается новый класс нейронных сетей: "Нелокальные интерпретируемые нейронные сети прямого счета" (нелокальные нейронные сети – ННС). Организация ННС обеспечивает один из вариантов решения традиционных для нейронных сетей проблем: содержательной интерпретации смысла интенсивности входных сигналов и весовых коэффициентов ("проблема интерпретируемости весовых коэффициентов"); содержательной интерпретации и обоснования аддитивности аргумента и вида активационной (передаточной) функции нейрона ("проблема интерпретируемости передаточной функции"); "Комбинаторного взрыва" при определении структуры связей нейронов, подборе весовых коэффициентов и передаточных функций ("проблема размерности"). Математическая модель ННС основана на предложенной автором системной теории информации и семантической информационной модели автоматизированного системно-когнитивного анализа (АСК-анализ), и в отличие от известных нейронных сетей, обеспечивают автоматизацию всех 10 базовых когнитивных операций, образующих "когнитивный конфигуратор". Предложены не только математическая модель, но также и соответствующий численный метод (включая алгоритмы и структуры данных), а также программный инструментарий нелокальных нейронных сетей (универсальная когнитивная аналитическая система "Эйдос" версии 9.0), успешно апробированные в ряде предметных областей. Данная система обеспечивает неограниченное количество слоев ННС при максимальном количестве весовых коэффициентов в слое до 16 миллионов (в текущей версии), до 4000 выходных нейронов, а также автоматическую визуализацию и запись в виде графических файлов сформированных моделей нелокальных нейронов и Паретто-подмножеств нелокальной нейронной сети.

Литература

1. Lutsenko E.V. Conceptual principles of the system (emergent) information theory & its application for the cognitive modelling of the active objects (entities) //2002 IEEE International Conference on Artificial Intelligence System (ICAIS 2002). –Computer society, IEEE, Los Alamos, California, Washington-Brussels-Tokyo, p. 268-269.

2. Бранский В.П. Философские основания проблемы синтеза релятивистских и квантовых принципов. –Л: ЛГУ, 1973. –175с.

3. Луценко Е. В. Автоматизированный системно-когнитивный анализ в управлении активными объектами (системная теория информации и ее применение в исследовании экономических, социально-психологических, технологических и организационно-технических систем): Монография (научное издание). – Краснодар: КубГАУ. 2002. – 605 с.

4. Луценко Е.В. Интерференция последствий выбора в результате одновременного выбора альтернатив и необходимость разработки эмерджентной теории информации. //В сб.: "Материалы III всероссийской межвузовской научно-технической конференции". – Краснодар: КВИ, 2002. – С.24-30.

5. Луценко Е.В. Теоретические основы и технология адаптивного семантического анализа в поддержке принятия решений (на примере универсальной автоматизированной системы распознавания образов "ЭЙДОС-5.1"). - Краснодар: КЮИ МВД РФ, 1996. - 280с.

6. Роберт Г.Джан, Бренда Дж.Данн. Границы реальности. (Роль сознания в физическом мире). /Пер. с англ. - М.: Объединенный институт высоких температур РАН, 1995. - 287с.

7. Цехмистро И.З. Поиски квантовой концепции физических оснований сознания. –Харьков: ХГУ, 1981. - 275с.

Научный электронный журнал КубГАУ . № 01(1), 2003