Научный электронный журнал КубГАУ . № 01(1), 2003

Имитационное моделирование ветроэнергетической установки

Богатырев Н.И., Креймер А.С.

Кубанский государственный аграрный университет

В последнее время большое внимание уделяется развитию возобновляемых источников энергии. В первую очередь это связано с повышением цен на органическое топливо, ухудшением экологической обстановки, появлением новых технологий в области нетрадиционных возобновляемых источников энергии. «Европейская энергетическая хартия», принятая 17 декабря 1991 года как политическая декларация 53 государств во многом предопределила направление развития энергетики Европы и мира в целом. Так, одним из положений хартии является обеспечение экологически чистого производства электроэнергии, которое возможно только в случае применения возобновляемых источников энергии.

Одним из наиболее перспективных видов возобновляемой энергетики является ветроэнергетика. Во всем мире примерно с 1980 года наблюдается непрерывный рост установленной мощности ВЭУ.

При проведении исследований в области ветроэнергетики часто бывает необходимо использовать различные модели, так натурные эксперименты не всегда возможны как по техническим, так и экономическим соображениям.

Математическая модель описывает реальный объект лишь с некоторой степенью приближения (детализации). При этом вид модели зависит как от природы исследуемого объекта, так и от задач исследования, методики моделирования, необходимой точности описания объекта. Общепринятым является разделение математического моделирования на три основных вида – аналитическое, имитационное и комбинированное [1, 2].

Характерной особенностью аналитического моделирования является запись процессов функционирования элементов моделируемой системы в виде некоторых соотношений – дифференциальных, интегро-дифференциальных, конечно-разностных, либо логических условий. Аналитическая модель может быть исследована следующими методами [3, 4].

1. Аналитическим. При этом целью является получение в общем виде различных зависимостей для искомых характеристик.

2. Численным. В этом случае целью является получение численных результатов при определенных начальных данных. Решение в общем виде не находится.

3. Качественным. Решение в явном виде отсутствует, но можно оценить некоторые свойства решения.

В отличие от аналитического моделирования принцип имитационного моделирования основывается на том, что математическая модель воспроизводит процесс функционирования во времени, причем имитируются элементарные события, протекающие в системе с сохранением логики их взаимодействия и последовательности протекания во времени. Таким образом, есть возможность получения по исходным данным сведения о состоянии системы в определенные промежутки времени, что позволяет оценить характеристики системы. Имитационное моделирование может быть положено в основу структурного, алгоритмического и параметрического синтеза больших систем, когда требуется создать систему с заданными характеристиками при определенных ограничениях, которая будет оптимальной по некоторым критериям оценки эффективности [2, 3].

С развитием вычислительной техники появилась возможность проводить достаточно точное моделирование различных систем. При этом значительно сокращаются расходы на проведение непосредственного эксперимента, так как многие параметры модели уточняются еще в ходе компьютерного моделирования. Кроме того, существует ряд задач, где постановка опыта на реальной модели просто невозможна или экономически неоправданна. В большинстве случаев современные средства моделирования позволяют обеспечить высокий уровень адекватности модели. Одним из таких средств является Simulink – интерактивный инструмент для моделирования, имитации и анализа динамических систем. Он дает возможность строить графические блок-диаграммы, имитировать динамические системы, исследовать работоспособность систем и совершенствовать проекты. Simulink полностью интегрирован с MATLAB®, обеспечивая доступ к широкому спектру инструментов анализа и проектирования.

Предлагается имитационная модель ветроэнергетической установки (ВЭУ) в Simulink для оценки вырабатываемой мощности.

Известно, что энергия, вырабатываемая ВЭУ пропорциональна энергии воздушного потока. Удельную мощность ветрового потока на единичную поверхность, перпендикулярную потоку W можно представить в следующем виде [5]:

(1)

Где р – средняя плотность воздуха (р = 1,225 кг/м₃ при Т=16⁰ С);

v – среднее значение скорости ветра, м/с.

Механическая энергия вращения ветроколеса W_м определяется коэффициентом использования энергии ветра (в иностранной технической литературе принят термин «коэффициент мощности») C_p.

(2)

Максимальная энергия, которую можно получить от идеального ветроколеса составляет примерно 59 % от кинетической энергии воздушного потока (закон Бетца–Жуковского), т.е. С_pMAX = 0.59. Для реальной турбины с горизонтальной осью вращения коэффициент мощности обычно находится в диапазоне 0.1 – 0.47 [5,6].

Быстроходность ветроколеса ВЭУ с горизонтальной осью вращения зависит от числа лопастей, угла тангажа и других факторов и определяется по известной формуле

(3)

где      ω – угловая скорость вращения ветроколеса;

             R – радиус ветроколеса;

             v – cкорость ветра.

Таким образом, мощность на валу ветроколеса можно определить по формуле

(4)

Момент на валу ветроколеса определяется из (3) и (4)

(5)

На основании приведенных соотношений построим зависимость мощности на валу ветроколеса от скорости ветра для определения рабочей скорости ВЭУ.

Наибольшую трудность вызывает аналитическое определение С_p ввиду чрезвычайной сложности и нелинейности аэродинамических процессов, возникающих при взаимодействии лопастей ветроколеса с потоками воздуха. Как правило, для заданного ветроколеса аэродинамический коэффициент моделируется с помощью специального программного обеспечения (PROPPC, WT_PERF и другие). Для получения C_p авторами использовалась программа WT_PERF и данные турбины с тремя лопастями, быстроходностью Z=9 и профилем NACA 4415 (аналогично серийно выпускаемой отечественной ВЭУ LMV – 3600). На рисунке 1 приведена зависимость C_p от скорости ветра. Для построения графика использовалась таблица, полученная в результате работы программы WT_PERF.

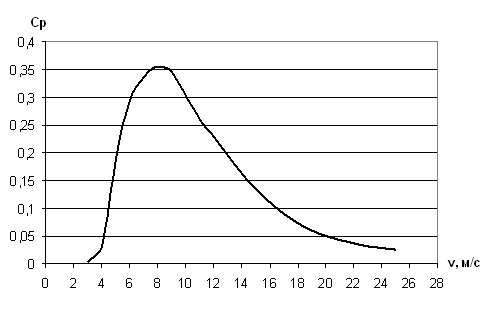
Рисунок 1 – Зависимость коэффициента C_p от скорости ветра

Как видно из диаграммы на рисунке 1, для данной турбины максимальный коэффициент использования энергии ветра достигается при скорости ветра примерно 8.5 м/c.

Как было показано выше, ввиду сложности аналитического вычисления C_p значительно удобнее имитационное его моделирование. Для оценки мощности, вырабатываемой ветроколесом, построим имитационную модель. Изменяемыми параметрами будет скорость ветра v и радиус ветроколеса R. Схема моделирования процесса приведена на рис. 2.

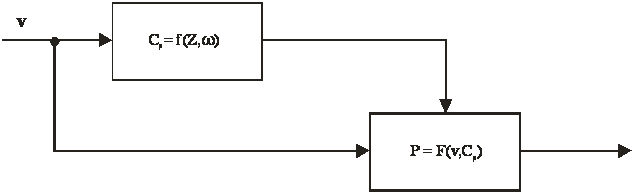
Рисунок 2 – Схема имитационной модели ВЭУ для получения зависимости P = f(v)

Для моделирования использовалось программное обеспечение из пакета MATLAB – Simulink. Зависимость С_p(v) реализована в виде блока Lookup Table и представляет собой  фактически табулированную функцию. Модель, построенная в Simulink приведена рис. 3.

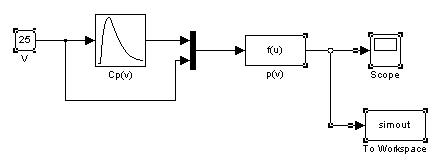
Рисунок 3 – Модель Simulink для получения завиcимости P(v)

Данные моделирования использованы для построения зависимости P(v) (радиусы ветроколеса – 2.5, 3.5 и 5 м) (рис. 4).

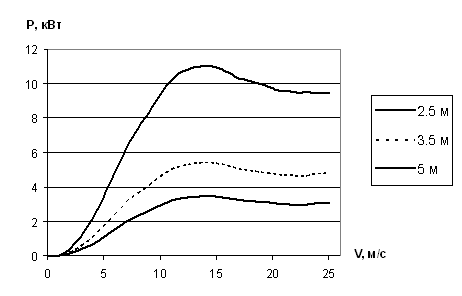
Рисунок 4 – Зависимость мощности на валу ветроколеса от скорости ветра и радиуса ветроколеса при постоянной частоте вращения

Полученные данные позволяют сделать следующие выводы.

1. Предлагаемую методику построения имитационной модели можно использовать для анализа мощности ВЭУ при различных скоростях ветра (в разных районах) и разных радиусах ветроколеса.

2.  Анализ исследований показывает, что при высоких скоростях ветра при поддержании постоянной угловой скорости вращения ветроколеса происходит снижение мощности, вырабатываемой ветроколесом. Данный факт обычно не учитывается при оценке средней мощности ВЭУ.

Литература

1. Веников В.А., Веников Г.В. Теория подобия и моделирования.- М.: Высшая школа, 1984.-439 с.
2. Советов Б.Я., Яковлев С.А.Моделирование систем. – М.: Высшая школа, 1999. – 271 с.
3. Симанков В.С., Зангиев Т.Т. Системный анализ при решении структурных задач альтернативной энергетики / Институт современных технологий и экономики. – Краснодар, 2001. – 151 с., ил.
4. Математическое моделирование: Методы, описания и исследования сложных систем / Под ред. А.А. Самарского. – М.: Наука, 1989. – 271 с.
5. Шефтер Я.И. Использование энергии ветра. – М.: Энергоатомиздат, 1983. – 200 с., ил.
6. Johnson G. Wind Energy Systems. New York, NY Prentice Hall, 1985. – 421 p.

Научный электронный журнал КубГАУ . № 01(1), 2003